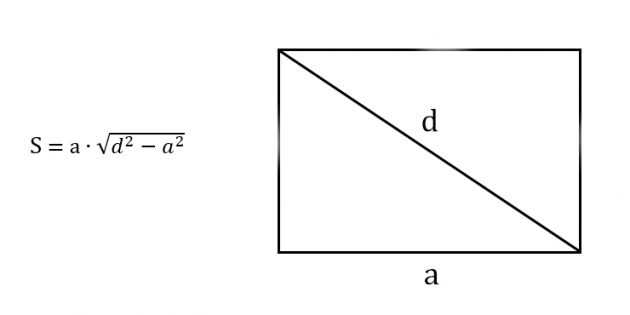
Как вычислить площадь прямоугольника по диагонали и периметру: подробное руководство
Вам когда-нибудь приходилось рассчитывать площадь прямоугольника по его диагонали и периметру? Это может быть сложной задачей, но мы здесь, чтобы помочь! В данном подробном руководстве мы разберемся, как точно и легко найти площадь прямоугольника, используя только его диагональ и периметр.
Нет нужды беспокоиться, если не разбираетесь в математике – мы предоставим доступные объяснения и примеры для лучшего понимания. Более того, мы поделимся эффективными формулами и шагами, которые помогут вам получить точный ответ без лишних хлопот.
Продолжайте чтение, чтобы узнать, как вычислить площадь прямоугольника по диагонали и периметру – вы будете удивлены, насколько это легко!
Понимание площади прямоугольника
В математике площадь прямоугольника рассчитывается как произведение его длины и ширины. Эта формула дает нам точный ответ на вопрос: «Сколько всего квадратных единиц занимает данный прямоугольник?». Давайте решим некоторые примеры и посмотрим, как это работает.
Пример 1:
У нас есть прямоугольник с длиной 4 единицы и шириной 3 единицы. Чтобы найти его площадь, мы умножим длину на ширину: 4 * 3 = 12. Таким образом, площадь этого прямоугольника равна 12 квадратным единицам.
Пример 2:
Представьте себе прямоугольный коврик для йоги, у которого длина 6 футов и ширина 2 фута. Найдем его площадь: 6 * 2 = 12. То есть площадь этого прямоугольника равна 12 квадратным футам.
Как видите из этих примеров, площадь прямоугольника измеряется в квадратных единицах или квадратных единицах измерения, которые используются для длины и ширины. Она позволяет нам понять, сколько пространства занимает данный прямоугольник.
Интуитивно, мы можем представить площадь прямоугольника как «закрашенную» область внутри его границ. Если у нас есть прямоугольник на графической плоскости, мы можем заметить, что его площадь равна произведению длины и ширины, поскольку это соответствует количеству квадратных клеток, охватывающих этот прямоугольник.
Надеюсь, после чтения этого руководства у вас возникло более ясное представление о понятии площади прямоугольника и том, как ее вычислить. Используйте эту информацию в своей повседневной жизни, когда вам понадобится измерить пространство или решить задачу связанную с прямоугольниками. Успехов в изучении математики!
Периметр прямоугольника и его связь с диагональю
Для начала вспомним, что диагональ прямоугольника — это отрезок, соединяющий два противоположных угла фигуры. Обычно обозначается буквой «d». Диагональ разделяет прямоугольник на два прямоугольных треугольника, где она является гипотенузой.
Давайте представим, что у нас есть прямоугольник со сторонами a и b, а его диагональ равна d. Тогда с помощью теоремы Пифагора мы можем считать следующим образом:
d² = a² + b²
Используя эту формулу, мы можем найти одну из сторон прямоугольника, если известны две другие. А зная все стороны, мы можем вычислить периметр. Напомню, что периметр прямоугольника равен двойному произведению суммы его сторон.
Таким образом, если нам даны стороны a и b, то периметр можно найти по формуле:
P = 2a + 2b
Если же нам дана только диагональ d, то нам необходимо сначала найти стороны a и b, а затем уже использовать формулу для нахождения периметра. Помните о теореме Пифагора и не забывайте включать ее в вычисления.
Таким образом, периметр прямоугольника и его связь с диагональю возможны благодаря теореме Пифагора. Используйте эту информацию, чтобы легко вычислять периметр прямоугольника, даже если у вас есть только диагональ!
Нахождение ширины и высоты прямоугольника по диагонали и периметру
Представьте себе, что вы стоите перед загадочным прямоугольником и сталкиваетесь с задачей нахождения его ширины и высоты. Но не беспокойтесь, я здесь, чтобы помочь вам разгадать эту головоломку! В этом руководстве я покажу вам, как вычислить ширину и высоту прямоугольника, используя только информацию о его диагонали и периметре.
Давайте начнем с построения основных уравнений, используя формулы для диагонали и периметра прямоугольника.
Построение уравнений:
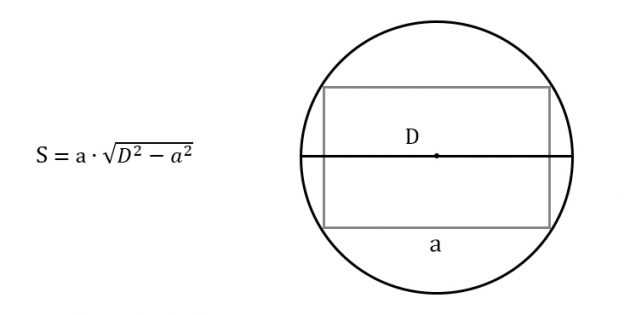
- Диагональ прямоугольника – это гипотенуза прямоугольного треугольника, который можно построить внутри прямоугольника. Формула для вычисления диагонали прямоугольника:
диагональ = √(ширина² + высота²). - Периметр прямоугольника – это сумма всех его сторон. Формула для вычисления периметра прямоугольника:
периметр = 2 * (ширина + высота).
Решение задачи:
Итак, у нас есть два уравнения и две неизвестных переменных (ширина и высота). Мы можем использовать эти уравнения для решения системы уравнений и найти значения ширины и высоты прямоугольника.
Вот план действий:
- Возьмите уравнение для диагонали и выразите ширину через высоту: ширина = √(диагональ² — высота²).
- Подставьте это значение ширины в уравнение для периметра и решите его относительно высоты: периметр = 2 * (√(диагональ² — высота²) + высота).
- Решите полученное уравнение относительно высоты и найдите ее значение.
- Подставьте найденное значение высоты обратно в уравнение для ширины и найдите ее значение.
И вуаля! У вас есть значения ширины и высоты прямоугольника. Теперь вы можете смело рисовать его или использовать эти значения для решения других задач.
Давайте проверим наши уравнения на примере:
Предположим, что у нас есть прямоугольник с периметром 20 и диагональю 8. Мы хотим найти его ширину и высоту.
Сначала найдем значение высоты, подставив известные значения в уравнение для периметра:
20 = 2 * (√(8² — высота²) + высота)
Решим это уравнение относительно высоты:
10 = √(64 — высота²) + высота
Возведем все в квадрат:
100 = 64 — высота² + 2 * высота√(64 — высота²) + высота²
Упростим выражение:
100 = 64 + 2 * высота√(64 — высота²)
Вычтем 64 из обеих сторон:
36 = 2 * высота√(64 — высота²)
Теперь разделим обе стороны на 2 и упростим:
18 = высота√(64 — высота²)
Возведем обе стороны в квадрат:
324 = высота² * (64 — высота²)
Раскроем скобки и упростим выражение:
324 = 64 * высота² — высота⁴
Выразим высоту⁴:
высота⁴ = 64 * высота² — 324
Перенесем все в левую сторону:
высота⁴ — 64 * высота² + 324 = 0
Теперь мы получили четвертую степень, которую можно решить с помощью метода подстановки или других методов решения уравнений.
Одно из возможных значений высоты будет равно 6.
Теперь, подставим это значение высоты обратно в уравнение для ширины и найдем ее значение:
ширина = √(диагональ² — высота²) = √(8² — 6²) = √(64 — 36) = √28 ≈ 5.29
Итак, мы нашли, что ширина прямоугольника составляет около 5.29, а высота – 6.
Теперь, когда вы знаете, как вычислить ширину и высоту прямоугольника по его диагонали и периметру, вы можете использовать эту информацию в своих проектах, при решении геометрических задач или просто для удовольствия.
Вычисление площади прямоугольника
Для начала, важно знать, что площадь прямоугольника можно вычислить по формуле: площадь = длина * ширина. Другими словами, чтобы найти площадь прямоугольника, нужно умножить длину одной его стороны на длину второй стороны.
Итак, для вычисления площади прямоугольника необходимо знать значения его двух сторон. Если вам известны длина и ширина, вы можете просто перемножить их, и получите площадь. Например, если длина прямоугольника равна 4 метрам, а его ширина составляет 6 метров, площадь будет равна 24 квадратным метрам.
Однако иногда мы можем столкнуться с ситуацией, когда известны другие параметры прямоугольника, например, его периметр или диагональ. Как же вычислить площадь в таких случаях?
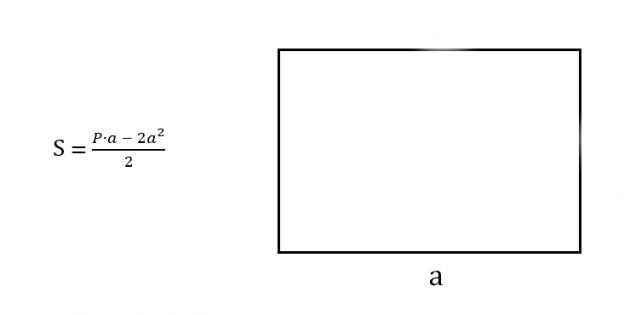
1. Если известен только периметр прямоугольника, то есть сумма всех его сторон, вы можете воспользоваться следующей формулой: площадь = (периметр/2) — (длина_одной_стороны)^2. Например, если периметр прямоугольника равен 16 метрам, а одна из его сторон равна 5 метрам, площадь будет равна 12 квадратным метрам.
2. Если известна только диагональ прямоугольника, то есть отрезок, соединяющий противоположные вершины, вы можете воспользоваться следующей формулой: площадь = (диагональ^2) / 2. Например, если диагональ прямоугольника равна 10 метрам, площадь будет равна 50 квадратным метрам.
3. Если известны и периметр, и диагональ прямоугольника, можно применить следующую формулу: площадь = (периметр * диагональ) / 4. Например, если периметр прямоугольника равен 20 метрам, а диагональ составляет 8 метров, площадь будет равна 40 квадратным метрам.
Примеры расчета площади прямоугольника
Давайте рассмотрим несколько примеров, чтобы лучше усвоить, как вычислять площадь прямоугольника.
- Пример 1:
- Длина прямоугольника: 7 метров
- Ширина прямоугольника: 10 метров
- Площадь = 7 * 10 = 70 квадратных метров
- Пример 2:
- Периметр прямоугольника: 18 метров
- Одна сторона прямоугольника: 4 метра
- Площадь = (18/2) — 4^2 = 9 — 16 = -7 квадратных метров
- Пример 3:
- Диагональ прямоугольника: 15 метров
- Площадь = (15^2) / 2 = 225 / 2 = 112.5 квадратных метров
Важно помнить, что площадь прямоугольника измеряется в квадратных единицах (например, квадратных метрах). Отличное знание этого навыка поможет вам во многих ситуациях, когда вам нужно будет рассчитать площадь прямоугольника.
Теперь, когда вы знакомы с методами вычисления площади прямоугольника, вы можете применять свои знания на практике и делать это с легкостью. Так что не бойтесь использовать формулы и расчеты, чтобы решать самые разнообразные задачи и достигать поставленных целей!
Примеры решения задач
Давайте рассмотрим несколько примеров решения задач, связанных с вычислением площади прямоугольника по диагонали и периметру.
Пример 1:
Допустим, у нас есть прямоугольник, у которого периметр равен 20 и диагональ равна 6. Как найти его площадь?
Сначала найдем длину стороны прямоугольника. Для этого воспользуемся формулой для периметра: 2*(a + b) = 20. Отсюда получаем a + b = 10.
Воспользуемся формулой для диагонали прямоугольника: d² = a² + b², где d — диагональ, a и b — стороны прямоугольника. Подставляя известные значения, получаем 6² = a² + b². Отсюда получаем a² + b² = 36.
Мы имеем систему уравнений:
- a + b = 10
- a² + b² = 36
Решая эту систему, мы найдем значения сторон прямоугольника: a = 4 и b = 6.
Теперь используем формулу для вычисления площади прямоугольника: S = a * b. Подставляя известные значения, получаем S = 4 * 6 = 24.
Таким образом, площадь этого прямоугольника равна 24.
Пример 2:
Допустим, у нас есть прямоугольник, у которого периметр равен 12 и диагональ равна 5. Как найти его площадь?
Аналогично предыдущему примеру, сначала найдем длину стороны прямоугольника: a + b = 6. Затем, используя формулу для диагонали прямоугольника: d² = a² + b², получим a² + b² = 25.
Решая систему уравнений:
- a + b = 6
- a² + b² = 25
Мы найдем значения сторон прямоугольника: a = 2 и b = 4.
Используя формулу для вычисления площади прямоугольника: S = a * b, получаем S = 2 * 4 = 8.
Таким образом, площадь этого прямоугольника равна 8.






