Когда нам нужно найти периметр сечения с заданными сторонами PM и KN, мы можем использовать определенные методы и формулы. Периметр сечения — это сумма всех сторон, ограничивающих данное сечение. Для его вычисления нам необходимо знать значения сторон PM и KN. Далее мы можем использовать простую математическую формулу для определения периметра, которая состоит из сложения длин всех сторон. Поэтому зная значения сторон PM и KN, мы сможем легко найти периметр сечения. Этот процесс является важным для различных областей, таких как строительство, архитектура и многих других.
Определение понятия «сечение» и его особенности
Одной из особенностей сечения является его форма. Сечение может быть круглым, прямоугольным, треугольным, овальным и другими. Форма сечения зависит от формы плоскости и объекта, с которым она пересекается. Например, при пересечении плоскости с цилиндром получается круглое сечение, а с кубом — прямоугольное.
Еще одной особенностью сечения является его размер. Размеры сечения определяются размерами плоскости и ее углом наклона относительно объекта. При более крутом угле наклона плоскости сечение может быть меньшего размера, а при менее крутом — большего размера. Например, при пересечении плоскости с прямоугольным параллелепипедом сечение будет иметь размеры, соответствующие сторонам этого параллелепипеда.
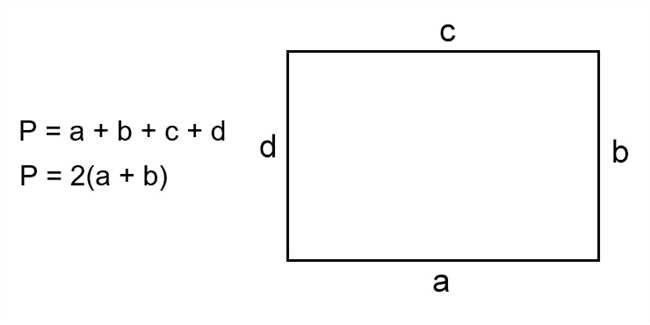
Также сечение имеет свой периметр, который определяется длиной всех его сторон. Периметр сечения может быть вычислен, если известны его форма и размеры. Например, для круглого сечения периметр равен длине окружности, а для прямоугольного — сумме длин всех его сторон.
Сечение имеет важное значение в различных областях, таких как архитектура, инженерное дело, геометрия и другие. Оно позволяет анализировать форму и размеры объектов, а также прогнозировать их взаимодействие с другими структурами или материалами.
Расчёт периметра сечения с использованием сторон PM и KN
Если сечение имеет форму прямоугольника, то периметр можно найти следующим образом: суммируем длины всех его сторон. В данном случае, если PM — одна сторона, а KN — противоположная сторона прямоугольника, периметр можно найти по формуле: периметр = 2 * PM + 2 * KN.
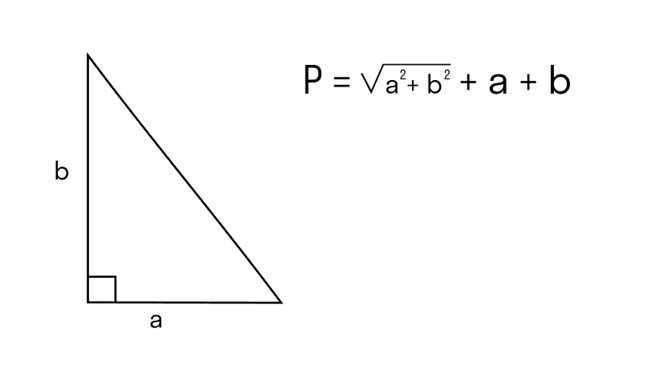
Если сечение имеет форму треугольника, то для его периметра нужно сложить длины всех трех его сторон. Опять же, если PM — одна сторона треугольника, а KN — другая сторона, периметр можно найти следующим образом: периметр = PM + KN + длина третьей стороны.
Но что делать, если сечение имеет сложную форму или не является ни прямоугольником, ни треугольником? В таком случае, для расчета периметра понадобится более сложные методы, такие как интегрирование или аппроксимация кривых. Эти методы требуют определенных математических навыков и инструментов, поэтому рекомендуется обратиться к специалисту или использовать специализированные программы или онлайн-калькуляторы для расчета периметра сложных сечений.
Примеры решения задач с нахождением периметра сечения

В данной статье мы рассмотрели несколько примеров задач, связанных с нахождением периметра сечения. Во всех этих задачах нам были известны стороны PM и KN, и нам требовалось найти их общий периметр.
Первый пример представлял собой задачу о двух параллельных и равных отрезках PM и KN, находящихся на одной плоскости. Для решения этой задачи нам было достаточно просто суммировать длины этих отрезков, так как они были равны. Поэтому периметр сечения составлял сумму длин PM и KN.
Во втором примере нам были известны стороны PM и KN, и нам требовалось найти периметр сечения, если известно, что сторона PM в два раза больше стороны KN. Для решения этой задачи нам пришлось использовать пропорции. Мы выразили длину стороны KN через длину стороны PM с помощью пропорции и найденное значение подставили в формулу для нахождения периметра сечения. Таким образом, получившееся выражение давало искомый периметр.
Третий пример был связан с нахождением периметра сечения, если нам известны углы, образованные пересечением отрезков PM и KN. В этом случае мы использовали свойства геометрических фигур, таких как прямоугольники и треугольники, чтобы найти длины оставшихся сторон с помощью тригонометрических функций. После этого мы просто суммировали длины всех сторон, чтобы получить периметр сечения.
Таким образом, наши рассмотренные примеры показывают разные методы решения задач с нахождением периметра сечения. Важно помнить, что в каждой задаче необходимо анализировать данные и применять соответствующие геометрические концепции и формулы для нахождения периметра.






