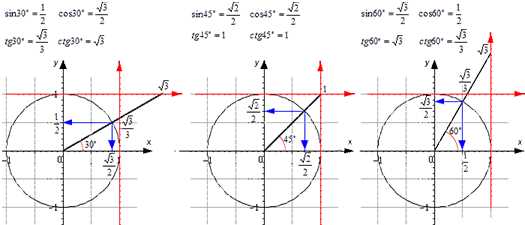
Как вычислить котангенс, если известен тангенс? Простой способ вычисления котангенса из тангенса

Как вычислить котангенс, если известен тангенс?

Тангенс и котангенс – это две взаимообратные тригонометрические функции, которые широко используются в математике и физике. Тангенс определяется отношением противоположной и прилегающей сторон в треугольнике, а котангенс является обратной функцией к тангенсу. Если известно значение тангенса, можно найти котангенс, применив соответствующую формулу. Для этого необходимо поделить единицу на значение тангенса. Например, если тангенс угла равен 0.5, то котангенс будет равен 2. Это позволяет легко вычислить котангенс, зная только тангенс.

Тангенс и его определение

Для определения тангенса необходимо знать длину противоположной и прилежащей сторон треугольника. Для непрямоугольных треугольников, коэффициент тангенса можно определить как отношение синуса угла к косинусу этого же угла.

Если имеется прямоугольный треугольник, то значение тангенса можно определить как отношение длины противоположной стороны к длине прилежащей стороны:

• Тангенс угла α = |противоположная сторона| / |прилежащая сторона|

Таким образом, зная длину противоположной стороны и длину прилежащей стороны, можно вычислить значение тангенса угла.

Тангенс имеет несколько особенностей. Во-первых, тангенс любого угла не может быть меньше -1 и больше 1. То есть, если значение тангенса превышает эти границы, необходимо проверить правильность вычислений.

Вторая особенность тангенса заключается в его периодичности. Значение функции тангенса повторяется каждые π радиан (или 180 градусов).

Третья особенность тангенса связана с его точками разрыва. Тангенс имеет точки разрыва при значениях угла, кратных π/2 (или 90 градусов). В этих точках тангенс становится бесконечным и не имеет определенного значения. Так, когда угол равен 90 градусов, тангенс невозможно определить.

Используя определение тангенса, вы можете легко вычислить его значение, если известны длины противоположей и прилежащей сторон треугольника или значения синуса и косинуса угла.

Что такое котангенс и его связь с тангенсом?

А что такое котангенс? Котангенс является взаимной функцией тангенса. Он также показывает нам, насколько крутой или пологой является угол. Если тангенс равен отношению противоположной и прилежащей сторон, то котангенс равен отношению прилежащей и противоположной сторон.

Как же связаны эти две функции? Их связь состоит в том, что тангенс и котангенс являются взаимными функциями. В математическом смысле это означает, что если мы знаем значение тангенса угла, мы можем легко вычислить его котангенс.

Давайте представим, что у нас есть прямоугольный треугольник, у которого известен тангенс угла. Мы можем использовать эту информацию, чтобы найти значение котангенса. Для этого нам необходимо взять обратное значение тангенса, чтобы получить котангенс.

Формула вычисления котангенса:

• Котангенс угла равен обратному значению тангенса угла.
• Математически это записывается следующим образом: котангенс угла = 1 / тангенс угла.

Пример:

Предположим, что у нас есть треугольник с углом 30 градусов. Мы знаем, что тангенс этого угла равен 1 / √3 (так как противоположная сторона равна 1, а прилежащая сторона равна √3 по теореме Пифагора). Чтобы найти котангенс, мы берем обратное значение тангенса и получаем 1 / (1 / √3), что равно √3.

Таким образом, котангенс угла 30 градусов равен √3.

Надеюсь, теперь вы понимаете, что такое котангенс и как его вычислить, если известен тангенс угла. Эти функции тесно связаны друг с другом и помогают нам анализировать и изучать треугольники и углы. Символично, что тангенс и котангенс являются взаимными функциями, ведь взаимопонимание и взаимосвязь – это важные аспекты в любых отношениях, включая отношения чисел и формул.

Формула для вычисления котангенса через тангенс

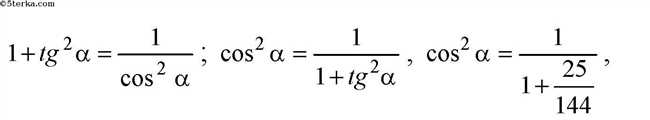
Формула для вычисления котангенса через тангенс выглядит следующим образом:

cot(x) = 1 / tan(x)

Для любого угла х, можно использовать данную формулу, чтобы получить значение котангенса. Просто найдите значение тангенса данного угла и возьмите его обратное значение.

Пример:

Предположим, что мы знаем, что tan(x) = 0,5. Чтобы вычислить котангенс этого угла, мы просто возьмем обратное значение тангенса:

1. Возьмем обратное значение тангенса: 1 / 0,5 = 2.

Таким образом, котангенс угла x равен 2.

Также можно использовать табличные значения для вычисления котангенса через тангенс. В табличных значениях есть соответствия между углами и значениями тригонометрических функций. Если известно значение тангенса угла, можно найти соответствующее значение котангенса через таблицу тригонометрических функций.

Например, если известно, что tan(x) = 1,732, то можно найти соответствующее значение котангенса в таблице. В таблице можно найти значение котангенса для угла, близкого к 60 градусам, и получить ответ.

Примеры вычисления котангенса по известному тангенсу

cot(x) = 1 / tan(x)

Где x — угол, а tan(x) — его тангенс.

Давайте рассмотрим несколько примеров вычисления котангенса:

1. Пример 1:

   • У нас есть угол x, для которого известен тангенс.
   • Пусть tan(x) = 1.
   • Используя формулу cot(x) = 1 / tan(x), получаем cot(x) = 1 / 1 = 1.
   • Таким образом, котангенс угла x равен 1.

2. Пример 2:

   • У нас есть угол y, для которого известен тангенс.
   • Пусть tan(y) = -1.5.
   • Используя формулу cot(y) = 1 / tan(y), получаем cot(y) = 1 / (-1.5) = -2/3.
   • Таким образом, котангенс угла y равен -2/3.

3. Пример 3:

   • У нас есть угол z, для которого известен тангенс.
   • Пусть tan(z) = 2.5.
   • Используя формулу cot(z) = 1 / tan(z), получаем cot(z) = 1 / 2.5 = 2/5.
   • Таким образом, котангенс угла z равен 2/5.

Вычисление котангенса по известному тангенсу позволяет нам определить значение угла, а также использовать результаты в различных математических расчетах и задачах.