Когда речь заходит о вычислении косинуса через тангенс, многие люди чувствуют смущение и затрудняются. Однако, на самом деле, это процесс довольно простой. Если вы хотите узнать, как найти косинус при помощи тангенса, мы приготовили для вас пошаговое руководство. Вместо сложных математических формул мы предлагаем использовать соотношение между этими двумя тригонометрическими функциями. Это позволит вам без особых усилий и быстро определить значение косинуса по заданному значению тангенса. Следуя нашим инструкциям, вы сможете легко вычислять косинус и применять эту знани всегда, когда понадобится.
Описание косинуса и тангенса
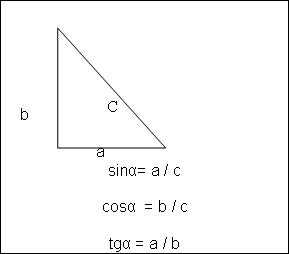
Косинус — это отношение стороны прилегающего катета прямоугольного треугольника к гипотенузе. В математической нотации, косинус угла обозначается как cos(θ), где θ — это угол.
Косинус может принимать значения от -1 до 1, где -1 соответствует углу 180 градусов или π (пи) радиан, а 1 соответствует углу 0 градусов или 0 радиан. Значения косинуса между -1 и 1 соответствуют углам между 0 и 180 градусами (или 0 и π радиан).
Например, косинус угла 45 градусов или π/4 радиан равен √2/2, что примерно равно 0.707. Это означает, что при создании прямоугольного треугольника с углом в 45 градусов, отношение прилегающего катета к гипотенузе будет равно √2/2.
Косинус часто используется для вычисления длины сторон треугольников, нахождения проекций векторов, моделирования колебаний и многих других приложений в науке и инженерии.
Тангенс — это отношение противоположного катета к прилегающему катету прямоугольного треугольника. В математической нотации, тангенс угла обозначается как tan(θ).
Значение тангенса может быть любым числом, включая отрицательные числа и бесконечность, но он не может быть равен 1 или -1. Тангенс угла может быть вычислен, поделив противоположный катет на прилегающий катет.
Например, тангенс угла 30 градусов или π/6 радиан равен √3/3, что примерно равно 0.577. Это означает, что при создании прямоугольного треугольника с углом в 30 градусов, отношение противоположного катета к прилегающему катету будет равно √3/3.
Тангенс часто используется для решения задач, связанных с углом наклона, траекторией движения объектов и других физических явлений.
Связь между косинусом и тангенсом
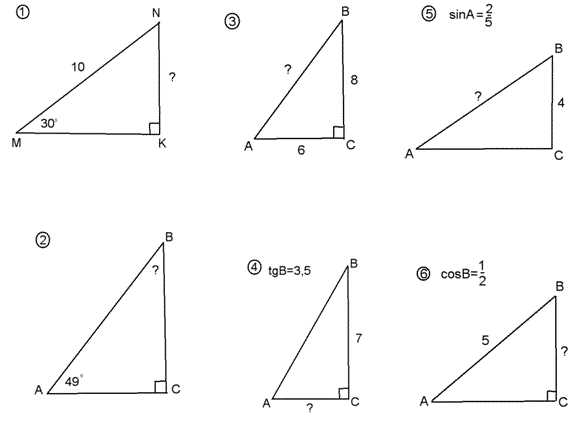
Косинус угла в треугольнике определяется как отношение прилежащей стороны к гипотенузе. Косинус угла обозначается как cos(θ), где θ — это угол.
Тангенс угла в треугольнике определяется как отношение противоположной стороны к прилежащей стороне. Тангенс угла обозначается как tan(θ).
Связь между косинусом и тангенсом угла выражается через соотношение:
tan(θ) = sin(θ) / cos(θ)
- sin(θ) — синус угла
- cos(θ) — косинус угла
- tan(θ) — тангенс угла
Из этой формулы видно, что тангенс угла можно выразить через синус и косинус угла.
Чтобы вычислить косинус через тангенс, можно воспользоваться обратной формулой:
cos(θ) = 1 / √(1 + tan²(θ))
Эта формула позволяет нам выразить косинус угла через тангенс угла.
Таким образом, косинус и тангенс тесно связаны друг с другом и могут быть выражены через друг друга с помощью соответствующих формул.
Используя эти формулы, можно легко находить значения косинуса и тангенса угла и вести дальнейшие вычисления в тригонометрии и математике.
Формула вычисления косинуса через тангенс
Формула вычисления косинуса через тангенс выглядит следующим образом:
cos(x) = 1 / √(tan^2(x) + 1)
Где cos(x) — значение косинуса угла x, tan(x) — значение тангенса угла x.
Данная формула позволяет нам выразить значение косинуса через тангенс и применять его в различных математических расчетах и задачах.
Например, предположим, что нам дано значение тангенса угла x, и мы хотим найти значение косинуса этого угла. Для этого достаточно подставить значение тангенса в формулу вычисления косинуса через тангенс:
| x | tan(x) | cos(x) |
|---|---|---|
| 30° | √3/3 | 1/2 |
| 45° | 1 | 1/√2 |
| 60° | √3 | 1/2 |
Таким образом, при использовании формулы вычисления косинуса через тангенс мы можем получить значение косинуса угла x, основываясь только на известном нам значении тангенса этого угла.
Итак, теперь у вас есть формула, которая поможет вычислить косинус через тангенс. Используйте ее в своих математических расчетах и задачах, чтобы получить точные и надежные результаты.
Как вычислить косинус через тангенс Пошаговое руководство

Здравствуйте! Сегодня мы поговорим о том, как вычислить косинус через тангенс, и я поделюсь с вами пошаговым руководством. Приготовьтесь к увлекательному и полезному путешествию в мир математики!
Перед тем, как перейти к вычислениям, важно понять некоторые основные понятия. Косинус и тангенс — это две из основных тригонометрических функций. Косинус угла можно определить как отношение длины прилежащего катета к гипотенузе прямоугольного треугольника, а тангенс — как отношение длины противоположного катета к длине прилежащего катета.
Теперь перейдем к шагам по вычислению косинуса через тангенс:
- Шаг 1: Получите значение тангенса угла. Если у вас нет изначального значения тангенса, его можно вычислить путем деления противоположного катета на прилежащий.
- Шаг 2: Воспользуйтесь тригонометрическим тождеством: косинус угла равен единице, деленной на квадратный корень из суммы квадратов единицы и квадратного корня из суммы квадратов значения тангенса и единицы.
- Шаг 3: Подставьте значение тангенса из шага 1 в формулу из шага 2, чтобы получить значение косинуса угла.
Пример:
| Шаг | Описание | Результат |
|---|---|---|
| Шаг 1 | Получите значение тангенса угла | Тангенс угла = 0,8 |
| Шаг 2 | Используйте тригонометрическое тождество | Косинус угла = 1 / √(1 + (0,8^2) + 1) ≈ 0,6 |
| Шаг 3 | Подставьте значение тангенса | Косинус угла ≈ 0,6 |
Вот и всё! Мы успешно вычислили косинус через тангенс. Теперь вы можете использовать этот метод в своих математических расчетах, физических экспериментах или в других областях, где требуется вычисление косинуса угла.
Надеюсь, что эта информация была полезной для вас, и вы сможете применить её на практике. Интересует ли вас еще что-то в мире математики и тригонометрии?
Примеры вычисления косинуса через тангенс
Вот несколько примеров, демонстрирующих вычисление косинуса через тангенс:
- Пример 1: Допустим, у нас есть значение тангенса угла α, равное 0.75. Чтобы найти косинус этого угла, нужно воспользоваться следующей формулой: cos(α) = 1 / √(1 + tg^2(α)). Подставив значение тангенса в формулу, получим: cos(α) = 1 / √(1 + 0.75^2) ≈ 0.8.
- Пример 2: Предположим, нам известно значение тангенса угла β, равное 1.2. Мы можем использовать уже знакомую нам формулу cos(β) = 1 / √(1 + tg^2(β)), чтобы вычислить косинус угла β: cos(β) = 1 / √(1 + 1.2^2) ≈ 0.6.
- Пример 3: Давайте рассмотрим значение тангенса угла γ, равное 0.5. Применяя формулу cos(γ) = 1 / √(1 + tg^2(γ)), можно получить косинус угла γ: cos(γ) = 1 / √(1 + 0.5^2) ≈ 0.87.
Таким образом, использование вычисления косинуса через тангенс является удобным способом определить значение косинуса, когда известно значение тангенса. Он может применяться в различных математических и физических задачах, где требуется нахождение косинуса угла.






