Как умножать и делить степени: правила и особенности операций

Особенности и правила умножения и деления степеней

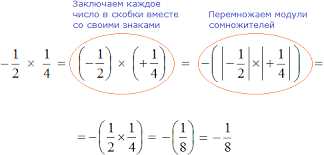
Умножение степеней с одинаковыми основаниями

Если основания степеней одинаковы, то для их умножения нужно умножить основание и сложить показатели степеней. Например, 2 в степени 3 умножить на 2 в степени 4 будет равно 2 в степени (3 + 4), то есть 2 в степени 7. Это правило можно записать как a в степени m умножить на a в степени n равно a в степени (m + n).

Умножение степеней с разными основаниями

Если у вас есть степени с разными основаниями, их умножать непосредственно нельзя. Но можно переписать эти степени в удобной форме, чтобы все основания стали одинаковыми. Например, умножение 2 в степени 3 на 3 в степени 3 можно переписать как (2 * 3) в степени 3, то есть 6 в степени 3. Это правило можно записать как a в степени m умножить на b в степени m равно (a * b) в степени m.

Деление степеней с одинаковыми основаниями

Если у вас есть степени с одинаковыми основаниями, то для их деления нужно разделить основание и вычесть показатели степеней. Например, 5 в степени 6 делить на 5 в степени 4 будет равно 5 в степени (6 — 4), то есть 5 в степени 2. Это правило можно записать как a в степени m поделить на a в степени n равно a в степени (m — n).

Деление степеней с разными основаниями

Если у вас есть степени с разными основаниями, их делить непосредственно нельзя. Вы можете переписать эти степени в удобной форме, чтобы все основания стали одинаковыми. Например, деление 4 в степени 5 на 2 в степени 5 можно переписать как (4 / 2) в степени 5, то есть 2 в степени 5. Это правило можно записать как a в степени m поделить на b в степени m равно (a / b) в степени m.

Также стоит отметить, что при умножении или делении степеней с отрицательными показателями следует использовать правила для работы с отрицательными числами. Например, (-2) в степени 3 умножить на (-2) в степени 4 будет равно (-2) в степени (3 + 4), то есть (-2) в степени 7. Такие операции требуют внимания и аккуратности, чтобы не допустить ошибок.

Запомните эти особенности и правила умножения и деления степеней, и они помогут вам легко и уверенно выполнять эти операции. Практикуйтесь в решении примеров и задач, чтобы закрепить свои навыки и применять их в реальных ситуациях. Успехов в изучении математики!

Умножение степеней

Теперь, когда мы понимаем важность умножения степеней, давайте разберемся, как правильно выполнять эту операцию. Для начала, давайте вспомним основные правила умножения:

• Умножение чисел с одинаковым основанием: если у нас есть две степени с одинаковым основанием, то мы просто складываем показатели степени. Например, a^n * a^m = a^(n+m). Это правило позволяет нам сократить выражения с одинаковыми основаниями и объединить их в одну степень.
• Умножение степени на число: когда мы умножаем степень на число, мы просто умножаем показатель степени на это число. Например, (a^n) * m = a^(n*m). Это правило дает нам возможность перемножить степень и число и получить новое выражение в виде степени.

Теперь давайте рассмотрим несколько примеров, чтобы посмотреть, как работают эти правила в действии.

Пример 1: Умножение степеней с одинаковым основанием

Рассмотрим выражение a^2 * a^3. В соответствии с правилом умножения степеней с одинаковым основанием, мы складываем показатели степеней, получая a^(2+3) = a^5. Таким образом, a^2 * a^3 = a^5.

Пример 2: Умножение степени на число

Рассмотрим выражение (b^2) * 4. Согласно правилу умножения степени на число, мы умножаем показатель степени на число, получая b^(2*4) = b^8. Таким образом, (b^2) * 4 = b^8.

Такие правила умножения степеней помогают нам упростить сложные выражения и получить более легкую для понимания форму. Они являются основой для решения задач и применения математических концепций в реальной жизни. Но помни, что эти правила работают только в случае, когда у нас нет других операций, например сложения или вычитания, внутри степеней.

Так что давай использовать эти правила и умножать степени с уверенностью! Практика делает мастера, поэтому решай больше задач и становись более опытным в умножении степеней. Уверен, ты справишься!

Правила умножения степеней

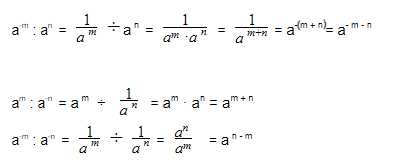
Правило #1: Умножение степени на степень

Когда нужно умножить две степени с одинаковыми основаниями, мы должны сохранить основание и сложить показатели степени. Например:

a^m * aⁿ = a^m+n

Давайте рассмотрим пример, чтобы проиллюстрировать правило:

a³ * a² = a³⁺² = a⁵

В этом примере мы умножили a в степени 3 на a в степени 2, что привело к a в степени 5.

Правило #2: Умножение степени на число

Когда нужно умножить степень на число, мы должны сохранить основание степени и умножить показатель степени на число. Например:

a^m * b = a^m * b

Давайте рассмотрим пример, чтобы проиллюстрировать правило:

a² * 3 = a² * 3

В этом примере мы умножили a в степени 2 на число 3, и результат остается a в степени 2, умноженным на 3.

Правило #3: Умножение степени на степень, где основания разные

Когда нужно умножить две степени с разными основаниями, мы должны сохранить оба основания и перемножить показатели степени. Например:

a^m * bⁿ = a^m * bⁿ

Давайте рассмотрим пример, чтобы проиллюстрировать правило:

a² * b³ = a² * b³

В этом примере мы умножили a в степени 2 на b в степени 3, и результат остается a в степени 2, умноженное на b в степени 3.

Теперь, когда вы знакомы с правилами умножения степеней, вы можете использовать их для упрощения и ускорения математических вычислений. Помните, что эти правила применимы только при умножении, а не при делении степеней.

Деление степеней

В математике операция деления степеней имеет свои особенности и правила, которые необходимо знать и уметь применять. Деление степеней можно встретить при работе с алгебраическими выражениями, уравнениями и в различных физических задачах.

Основное правило деления степеней заключается в том, что при делении степеней с одинаковым основанием необходимо вычитать их показатели степени:

a^m : aⁿ = a^{m — n}

Здесь a — основание степени, m и n — показатели степени.

При делении одной степени на другую степень с разными основаниями, необходимо привести выражение к общему основанию. Например:

a^m : bⁿ = (a^m)/(bⁿ)

В этом случае необходимо умножить числитель и знаменатель на одинаковую степень основания, чтобы получить общий знаменатель.

Также следует помнить о правиле деления степени на число. Если делитель равен одному, то показатель степени остается без изменений:

a^m : 1 = a^m

Правила деления степеней играют важную роль в математике и позволяют упростить выражения, решать уравнения и доказывать различные теоремы. Используя эти правила, можно легко решать задачи, требующие использования степеней.