Как составить и вычислить пропорцию с процентами: пошаговая инструкция и примеры

Пропорции с процентами – это математический инструмент, который позволяет определить соотношение значений с использованием процентов. Чтобы составить и вычислить пропорцию с процентами, необходимо следовать нескольким шагам. Во-первых, определите, какие значения вы хотите сравнить и какой процент вы хотите использовать. Затем установите пропорцию, где известное значение будет соответствовать 100%, а неизвестное значение будет соответствовать проценту, который вы хотите найти. Затем решите уравнение, чтобы найти нужный процент. Например, если вы хотите вычислить 20 процентов от числа 50, вы можете записать пропорцию как 50/100 = x/20 и решить уравнение для x. Правильно составленная и вычисленная пропорция с процентами поможет вам легко и точно определить соотношение значений.

Определение пропорции с процентами

Для понимания пропорции с процентами рассмотрим пример. Предположим, у вас есть кошелек с 100 долларами. Вы тратите 20% от общей суммы на покупку продуктов. Какую сумму вы потратите?

Чтобы ответить на этот вопрос, нужно использовать пропорцию с процентами. В данном случае, 20% от 100 долларов можно записать как 20/100. Для нахождения суммы, которую вы потратите, нужно умножить 100 на результат деления 20/100:

100 * (20/100) = 20

Таким образом, вы потратите 20 долларов на покупку продуктов.

Пропорция с процентами также может быть использована для определения процентного соотношения между двумя значениями. Например, предположим, у вас 500 долларов и ваши расходы составляют 200 долларов. Какой процент от общей суммы составляют ваши расходы?

Для решения этой задачи нужно использовать пропорцию с процентами. В данном случае, процентное соотношение можно записать следующим образом:

200 / 500 * 100 = 40

Таким образом, ваши расходы составляют 40 процентов от общей суммы.

Пропорция с процентами — это математическое понятие, которое позволяет определить отношение одного числа к другому в процентном соотношении. Она может быть использована для расчетов в различных сферах, а также в повседневной жизни. Зная основные принципы пропорции с процентами, можно легко решать задачи связанные с расчетами процентного соотношения или определением конкретного значения в процентах от общей суммы. Важно помнить, что при использовании пропорции с процентами необходимо учитывать все известные значения и грамотно их применять в формуле расчета. Это поможет получить правильный и точный результат.

Что такое пропорция с процентами?

Пропорция с процентами состоит из двух частей: базового значения и процента. Базовое значение – это общее значение, от которого мы берем процент, а процент представляет собой часть или долю от базового значения.

Например, допустим, у нас есть базовое значение – сумма денег, которую мы хотим разделить на две части. Мы хотим узнать, сколько процентов составляет каждая часть от всей суммы. Пропорция с процентами поможет нам найти ответ на этот вопрос.

Простейший способ вычисления пропорции с процентами – это умножение базового значения на процент и деление полученного значения на 100.

Пример:

У нас есть сумма денег – 1000 рублей. Мы хотим узнать, сколько процентов составляет 200 рублей от всей суммы. Для этого мы умножаем 1000 на 200 и делим на 100:

1. Умножение: 1000 * 200 = 200 000
2. Деление: 200 000 / 100 = 2000

Таким образом, 200 рублей составляют 20% от суммы в 1000 рублей.

Пропорция с процентами может быть использована для решения различных задач, включая расчет налогов, скидок, прибыли и других финансовых показателей. Она также может быть полезна при анализе статистических данных и оценке вероятностей.

Итак, пропорция с процентами – это мощный инструмент, который позволяет нам легко определить отношение процентов к базовому значению. Ее использование поможет нам делать более информированные решения и улучшать наши финансовые навыки. Вы можете применять ее в различных ситуациях для решения разнообразных задач. Попробуйте применить этот метод вычисления пропорции с процентами в своей повседневной жизни и посмотрите, как это может помочь вам принимать более осознанные решения.

Зачем нужна пропорция с процентами

Один из главных вопросов, на который отвечает пропорция с процентами, это «сколько?» Сколько процентов составляет отдельный элемент от целого? Например, сколько процентов площади поля составляют пшеничные ростки, или сколько процентов детей доходят до уровня грамотности в определенной стране. Ответы на такие вопросы позволяют нам понять, как изменяются пропорции в разных ситуациях и какие последствия это может иметь.

Кроме того, пропорция с процентами помогает нам принимать взвешенные решения. Например, если у nas есть ограниченный бюджет и нам нужно распределить его между различными проектами, пропорция с процентами позволит нам определить, сколько средств нужно выделить на каждый проект в зависимости от его значимости и приоритетности. Это позволяет нам максимально эффективно использовать ресурсы и достигать поставленных целей.

Шаги для составления пропорции с процентами

Составление и вычисление пропорции с процентами может показаться сложной задачей, но на самом деле это довольно просто. В этой статье я расскажу вам о нескольких шагах, которые помогут вам успешно составить и вычислить пропорцию с процентами.

Шаг 1: Определите известные и неизвестные значения

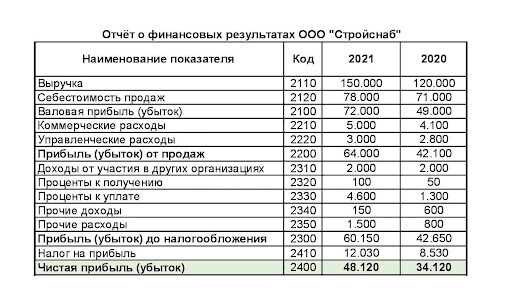
Прежде чем приступить к составлению пропорции с процентами, вам необходимо определить все известные и неизвестные значения. Известные значения — это числа или проценты, которые уже имеются у вас. Неизвестные значения — это числа или проценты, которые вы хотите найти.

Шаг 2: Установите соотношение между известными и неизвестными значениями

На этом шаге, вам нужно определить, какие известные и неизвестные значения связаны друг с другом. Например, если вы знаете процент скидки и стоимость товара до скидки, то можно установить соотношение между этими значениями.

Шаг 3: Запишите составленную пропорцию

После определения соотношения, вам необходимо записать составленную пропорцию. Пропорция состоит из двух долей, причем одна доля является известным значением, а другая — неизвестным. Пропорция может быть записана в виде дроби или в виде уравнения.

Шаг 4: Решите пропорцию

Наконец, пришло время решить составленную пропорцию. Для этого вы можете использовать правило трех, когда вы пропорционально умножаете и делите числа, чтобы найти неизвестное значение. Не забывайте, что проценты нужно привести к десятичной дроби, разделив значение на 100.

Пример

Давайте рассмотрим пример для лучшего понимания. Предположим, вы хотите вычислить сумму налога на прибыль вашей компании, зная, что налоговая ставка составляет 25%. Если прибыль вашей компании равна 100 000 рублей, какова будет сумма налога?

Шаг 1: Определите известные и неизвестные значения. Известные значения: налоговая ставка — 25%, прибыль — 100 000 рублей. Неизвестное значение: сумма налога.

Шаг 2: Установите соотношение между известными и неизвестными значениями. Налоговая ставка и сумма налога связаны друг с другом.

Шаг 3: Запишите составленную пропорцию. Налоговая ставка / 100 = сумма налога / прибыль.

Шаг 4: Решите пропорцию. 25 / 100 = сумма налога / 100 000. Умножаем 25 на 100 000 и делим на 100: 25 000 / 100 = сумма налога. Следовательно, сумма налога составляет 25 000 рублей.

Таким образом, вы успешно рассчитали сумму налога на прибыль вашей компании.

Определение известных и неизвестных значений

Пропорция — это отношение двух или более величин. В пропорции есть четыре величины: две известные и две неизвестные. Обычно пропорция записывается в виде a:b=c:d, где a и c — известные величины, а b и d — неизвестные.

Для решения пропорции с процентами нам необходимо определить значения для одной или нескольких неизвестных величин. При этом нам могут помочь следующие методы:

• Использование данных, предоставленных в условии задачи. В условии могут быть указаны известные значения или информация о процентах, которую мы можем использовать для расчетов.
• Использование формул и правил математики. Часто в задачах пропорций с процентами используются формулы для вычисления процентов или других величин. Знание этих формул может помочь нам определить неизвестные значения.
• Перепроверка расчетов. После расчетов мы должны перепроверить полученные значения, чтобы убедиться, что они верные и соответствуют условию задачи.

Важно помнить, что при решении пропорции с процентами необходимо аккуратно работать с процентами и десятичными дробями. Перевод процентов в десятичные дроби и наоборот — это важная часть вычислений.

Расстановка значений в пропорцию

Чтобы правильно составить и вычислить пропорцию с процентами, вы должны следовать нескольким шагам:

1. Определите изначально заданную пропорцию и запишите ее в форме a:b = c:d, где «a» и «b» — известные значения, а «c» и «d» — неизвестные значения, которые вы хотите найти.
2. Расставьте значения, известные вам, в соответствующие места в пропорции. Например, если известны значения «a» и «c», то запишите пропорцию в виде a:b = c:d.
3. Выберите одно из двух терминов для поиска (в данном случае «b» или «d»).
4. Умножьте «a» на «d» и «c» на «b» для получения новой пропорции вида ad = cb.
5. Выразите отсутствующее значение («b» или «d») путем разделения обеих частей пропорции на известные величины. Например, чтобы найти «b», поделите обе части пропорции на «a»: b = (ad) / c.
6. Вычислите значение неизвестной величины, используя известные значения и пропорцию.

Расстановка значений в пропорцию может показаться сложной на первый взгляд, но с практикой становится более простой и интуитивно понятной. Важно следовать шагам и не делать ошибок при выполнении вычислений.

Теперь, когда вы знаете, как правильно расставлять значения в пропорцию, вы можете использовать этот навык для решения различных математических задач. Практика и опыт помогут вам стать лучше в этом деле. Удачи в изучении математики!

Методика вычисления пропорции с процентами

Во-первых, для начала вычислений необходимо определить изначальное число или величину, к которой будет применяться пропорция. Затем следует определить процент этой величины, который будет использоваться в пропорции. Далее, следует установить связь между процентом и самой величиной путем использования знака процента (%) или десятичной дроби (например, 0,25 для 25%).

Для подсчета конечного результата, необходимо умножить изначальное число на процент или десятичную дробь, полученную на предыдущем шаге. Это даст нам значение, которое представляет собой процентную составляющую исходной величины. Чтобы вычислить конечный результат, следует прибавить или вычесть эту процентную составляющую в зависимости от постановки задачи.

Например, если мы хотим вычислить 15% от 200, мы умножаем 200 на 0,15 (или 15%) и получаем 30. Это означает, что 30 представляет собой 15% от 200. Если мы хотим найти 85% от 200, мы умножаем 200 на 0,85 и получаем 170. Ответ составляет 170, так как это 85% от 200.

Важно не путать процент изначальной величины с конечным результатом. Процент представляет собой только составляющую изначальной величины, которую можно добавить или вычесть при условии задачи.