Понимание того, как правильно складывать и вычитать положительные и отрицательные числа, является важной основой в математике. Правила для этих операций не такие сложные, как может показаться. Для сложения чисел с одинаковыми знаками нужно сложить их абсолютные значения и сохранить знак. В случае разных знаков, нужно вычесть абсолютные значения и сохранить знак числа с большим по модулю значением. Вычитание происходит путем изменения знака второго числа и сложения. Рассмотрим несколько примеров, чтобы лучше понять это правило и применять его в практике.
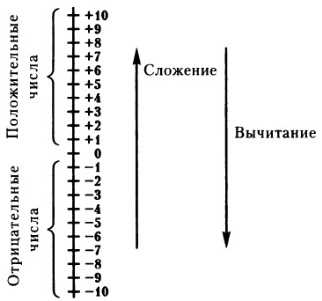
Положительные и отрицательные числа
В нашей повседневной жизни мы часто сталкиваемся с положительными и отрицательными числами. Они используются для описания различных ситуаций, например, температуры, финансовых операций, перемещения и т.д. Понимание того, как складывать и вычитать положительные и отрицательные числа, может пригодиться нам во многих сферах жизни.
Давайте сначала разберемся с понятиями положительных и отрицательных чисел. Положительное число – это число, которое больше нуля, а отрицательное число – меньше нуля. Например, число 5 является положительным, а число -3 является отрицательным.
Когда мы складываем положительное число с положительным числом, результат также будет положительным. Например, 5 + 3 = 8. Это простое правило, которое мы обычно знаем с детства.
Но что происходит, когда мы складываем положительное число с отрицательным числом? В этом случае необходимо учитывать знаки чисел. Если положительное число имеет больший модуль (абсолютное значение), то результат будет иметь знак этого числа, но будет ближе к нулю. Например, 5 + (-3) = 2. В этом случае сумма будет положительной и ближе к нулю, потому что положительное число имеет больший модуль.
Когда мы складываем отрицательное число с отрицательным числом, результат также будет отрицательным. Например, (-5) + (-3) = (-8). При сложении отрицательных чисел мы просто складываем их модули и затем приписываем им знак минус.
Что же происходит, когда мы вычитаем положительное число из положительного числа? В этом случае мы просто вычитаем одно число из другого и результат также будет положительным. Например, 5 — 3 = 2.
Но когда мы вычитаем положительное число из отрицательного числа, результат будет отрицательным. Например, (-5) — 3 = (-8).
Когда мы вычитаем отрицательное число из отрицательного числа, результат будет положительным. Например, (-5) — (-3) = (-2). Для выполнения этой операции мы можем сначала изменить знак вычитаемого числа на противоположный и затем сложить два числа.
Итак, мы разобрались, как складывать и вычитать положительные и отрицательные числа. Эти правила являются основными и легко запоминаются. Они помогут вам лучше понимать и использовать числа в различных ситуациях. Другими словами, понимание положительных и отрицательных чисел может быть полезно в финансовом планировании, управлении временем, обмене товарами и многих других областях жизни.
Запомните, что взаимодействие положительных и отрицательных чисел дает нам возможность более точно описывать и моделировать окружающий нас мир. Положительные и отрицательные числа — это не просто математические понятия, а инструменты для решения реальных задач. Используйте эту информацию в своей повседневной жизни и станьте уверенными в мире чисел!
Что такое положительные и отрицательные числа?
Здравствуй, друг! Сегодня мы поговорим о положительных и отрицательных числах. Давай разберемся, что они из себя представляют и как с ними работать.
Положительные числа — это числа, которые больше нуля. Они обозначают объекты, события или качества, которые мы считаем «хорошими» или «положительными». Давай возьмем для примера температуру: если термометр показывает +25 градусов, то это положительное число, которое обозначает тепло и комфорт.
А что насчет отрицательных чисел? Они меньше нуля и обозначают объекты, события или качества, которые мы считаем «плохими» или «отрицательными». Например, если температура за окном показывает -10 градусов, то это отрицательное число, которое говорит нам о холоде и непогоде.
Довольно просто запомнить, не правда ли? Но самое интересное начинается, когда мы начинаем складывать и вычитать положительные и отрицательные числа. Как тебе такая возможность?
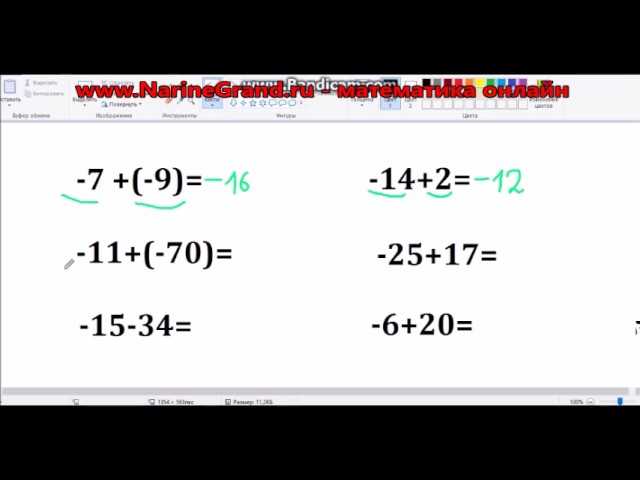
Итак, давай посмотрим на примеры:
- Если у нас есть +5 и мы прибавляем к нему -3, то получим 2. Плюс 5 минус 3 равно 2. Вообще, когда добавляем положительное число к положительному, результат будет положительным.
- А если у нас есть -7 и мы добавляем к нему +2, то тоже получим -5. Минус 7 плюс 2 даст нам минус 5. Когда прибавляем отрицательное число к отрицательному, результат также будет отрицательным.
- Но если мы снова возьмем -7 и вычтем из него -3, то получим -4. Минус 7 минус 3 равно минус 4. Когда вычитаем отрицательное число из отрицательного, результат становится больше нуля, то есть положительным.
Важно помнить, что положительные и отрицательные числа обладают определенными свойствами и правилами. При сложении или вычитании, знак числа важно учитывать. И надеюсь, что теперь ты лучше разобрался в этой теме и готов применить свои знания на практике!
Удачи в изучении! Буду рад помочь в ответе на другие вопросы!
Особенности положительных и отрицательных чисел
Рассмотрим некоторые особенности положительных и отрицательных чисел:
- Положительные числа: Положительные числа обозначаются без знака или с плюсом перед числом. Они представляют значения, большие или равные нулю. Например, число 5 является положительным числом. Положительные числа могут использоваться для измерения количества, времени, расстояния и других величин.
- Отрицательные числа: Отрицательные числа обозначаются с минусом перед числом. Они представляют значения, меньшие нуля. Например, число -3 является отрицательным числом. Отрицательные числа могут использоваться для отображения задолженностей, температур ниже нуля или любых других значений, которые находятся на обратной стороне от положительных чисел на числовой прямой.
Если мы складываем положительное число и положительное число, получаем сумму, которая больше обоих чисел. Например, 3 + 2 = 5. Это легко понять, потому что мы просто добавляем значения двух положительных чисел вместе.
Если мы складываем положительное число и отрицательное число, получаем разность между этими числами. Например, 3 + (-2) = 1. Поскольку мы добавляем положительное число и отрицательное число, мы вычитаем абсолютное значение отрицательного числа из положительного.
Вычитание положительных и отрицательных чисел осуществляется путем замены знака второго числа и добавления его к первому числу. Например, 3 — (-2) = 5. Мы меняем знак отрицательного числа и добавляем его к положительному числу.
Все эти правила основаны на математических принципах и являются универсальными. Они применяются в различных областях науки, техники и финансов. Понимание этих особенностей помогает нам правильно складывать и вычитать положительные и отрицательные числа в нашей повседневной жизни.
Итак, положительные и отрицательные числа являются неотъемлемой частью нашей жизни и помогают нам понять и описать мир вокруг нас. Используйте их с уверенностью и наслаждайтесь математикой!
Сложение положительных и отрицательных чисел
Перед тем, как мы начнем говорить о сложении положительных и отрицательных чисел, самое важное правило, которое нужно запомнить – знак сложения двух чисел зависит от их знаков.
Правила сложения
1. Если два числа имеют одинаковый знак (положительный или отрицательный), сложение выполняется так, будто это два положительных числа, а затем в конечном ответе сохраняется их исходный знак.
Например: 3 + 5 = 8 и -3 + (-5) = -8
2. Если одно число положительное, а другое отрицательное, сложение выполняется путем вычитания чисел по модулю и сохранения знака числа с большим модулем.
Например: 7 + (-4) = 7 — 4 = 3 и -7 + 4 = 4 — 7 = -3
3. Если одно число положительное, а другое ноль, сложение просто дает положительное число.
Например: 6 + 0 = 6 и -6 + 0 = -6
Примеры
Давайте рассмотрим несколько примеров для лучшего понимания сложения положительных и отрицательных чисел:
- Вычислим: 4 + (-8)
- Вычислим: -5 + 3
- Вычислим: -2 + (-2)
Так как числа имеют разные знаки, мы будем выполнять вычитание чисел по модулю и сохранять знак числа с большим модулем. Таким образом, 4 + (-8) = 4 — 8 = -4
Оба числа имеют разные знаки, поэтому мы выполняем сложение как вычитание чисел по модулю и сохраняем знак числа с большим модулем. Таким образом, -5 + 3 = 3 — 5 = -2
Оба числа имеют отрицательный знак, поэтому мы выполняем сложение как с положительными числами и сохраняем их исходный отрицательный знак. Таким образом, -2 + (-2) = -4
Это лишь некоторые основные примеры сложения положительных и отрицательных чисел. Однако, в реальной жизни встречаются более сложные и разнообразные задачи, где необходимо применять эти правила. Поэтому, чем больше вы будете практиковаться, тем более уверенно вы будете решать задачи по сложению положительных и отрицательных чисел.
Правила сложения
- Правило 1: Сложение одинаковых знаков
- Правило 2: Сложение чисел разных знаков
- Правило 3: Использование числовой линии
- Правило 4: Сложение более чем двух чисел
Если у нас есть два положительных числа или два отрицательных числа, мы складываем их абсолютные значения и приписываем итоговую сумму тому же знаку, с которым начали. Например: +5 + (+3) = +8 или -6 + (-2) = -8.
Если у нас есть положительное и отрицательное число, мы вычитаем меньшее абсолютное значение из большего абсолютного значения и используем знак числа с большим абсолютным значением. Например: +7 + (-2) = +5 или -4 + (+9) = +5.
Числовая линия — это инструмент, который помогает визуализировать сложение чисел, особенно чисел с разными знаками. Положительные числа представляются справа от нуля, а отрицательные числа — слева. При сложении двух чисел, мы перемещаемся вправо или влево на горизонтальной оси, в зависимости от их знака и абсолютного значения.
Если у нас есть более двух чисел для сложения, мы можем сложить их попарно, используя правила сложения, которые мы только что рассмотрели. Затем мы можем продолжить сложение сумм попарно, пока не получим итоговую сумму. Например: +2 + (+4) + (-3) + (-1) = +2 + (+1) = +3.
Теперь, когда вы знакомы с правилами сложения, вы можете применять их практически в любой ситуации. Используйте эти правила, чтобы правильно складывать положительные и отрицательные числа и получать точные результаты.
Примеры сложения
Пример 1:
Представьте, что у вас есть 2 яблока, а ваш друг дал вам еще 3 яблока. Сколько яблок у вас будет в итоге? Чтобы найти ответ, мы можем просто сложить количество яблок: 2 + 3 = 5. Получается, что у вас будет 5 яблок.
Пример 2:
Представьте ситуацию, где на вашем счете в банке было 100 долларов, а вы положили еще 50 долларов. Сколько денег у вас теперь на счете? Просто сложим числа: 100 + 50 = 150. Таким образом, у вас теперь на счету 150 долларов.
Пример 3:
Предположим, вы хотите сделать заказ в интернет-магазине и выбрали товары на сумму 1200 рублей и 800 рублей. Сколько общая сумма заказа? Сложим числа: 1200 + 800 = 2000. Таким образом, общая сумма заказа составляет 2000 рублей.
Примеры сложения помогают нам понять, как применять эту операцию в повседневных ситуациях. Они также помогают нам развивать навыки арифметики и логического мышления.
- Пример 1: 2 + 3 = 5
- Пример 2: 100 + 50 = 150
- Пример 3: 1200 + 800 = 2000
Вычитание положительных и отрицательных чисел

Вычитание положительных и отрицательных чисел может быть сложным и запутанным процессом, но с правильным пониманием правил и достаточной практикой, вы сможете справиться с ним без проблем. В этой статье мы разобрали основные правила и примеры вычитания положительных и отрицательных чисел, чтобы помочь вам улучшить свои математические навыки.
Основные правила вычитания положительных и отрицательных чисел:
- Вычитание положительного числа из положительного числа: просто вычетаем одно число из другого и записываем результат.
- Вычитание отрицательного числа из положительного числа: меняем знак отрицательного числа на положительный и проводим обычное вычитание.
- Вычитание положительного числа из отрицательного числа: меняем знак обоих чисел на противоположный и проводим обычное вычитание.
- Вычитание отрицательного числа из отрицательного числа: меняем знаки чисел на противоположный и проводим обычное вычитание.
Примеры вычитания положительных и отрицательных чисел:
| Пример | Решение | Ответ |
|---|---|---|
| 5 — 2 | Вычитаем 2 из 5 | 3 |
| 7 — (-3) | Меняем знак (-3) на (+3) и вычитаем из 7 | 10 |
| (-4) — 8 | Меняем знаки обоих чисел на противоположный и вычитаем | -12 |
| (-2) — (-5) | Меняем знаки обоих чисел на противоположный и вычитаем | 3 |
Запомните эти правила и не забывайте тренироваться, чтобы стать более уверенным в вычитании положительных и отрицательных чисел. Удачи вам в ваших математических приключениях!






