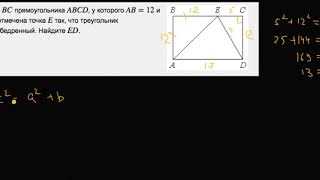
Как решить задачу с прямоугольником ABCD: AB12, AD17, BC?
Давайте взглянем на методы решения таких задач с прямоугольниками. Для начала, нам известны длины двух сторон прямоугольника AB и AD: AB равно 12, а AD равно 17. Нужно определить длину третьей стороны BC. Чтобы найти BC, мы можем воспользоваться теоремой Пифагора для треугольника ABC. Теорема гласит, что квадрат длины гипотенузы (в данном случае BC) равен сумме квадратов длин катетов (AB и AD). Применив теорему Пифагора, мы найдем значение BC и сможем решить задачу.
Описание задачи

Итак, у нас есть прямоугольник ABCD, и нам нужно найти его площадь. Известно, что сторона AB равна 12 единицам измерения, а сторона AD равна 17 единицам измерения. Наша задача — найти площадь этого прямоугольника.
Для решения этой задачи мы можем использовать простую формулу для расчета площади прямоугольника: площадь равна произведению длины одной стороны на длину другой стороны. В нашем случае, это будет AB * AD.
Чтобы найти площадь прямоугольника, нам нужно перемножить длину стороны AB (12) на длину стороны AD (17). Умножим эти числа: 12 * 17 = 204.
Таким образом, площадь прямоугольника ABCD равна 204 единицам площади. Ответ найден!
Мы успешно решили задачу и нашли площадь прямоугольника ABCD, используя простую формулу умножения. Надеюсь, это решение было полезным и понятным. Если у тебя возникли еще вопросы или ты хочешь поговорить о других математических задачах, буду рад помочь тебе! Удачи в изучении математики!
Условие задачи
Давайте рассмотрим задачу, в которой есть прямоугольник ABCD с известными сторонами: AB = 12 и AD = 17 (единицы измерения не указаны). Нашей задачей будет найти длины оставшихся двух сторон, BC и CD.
Мы знаем, что прямоугольник ABCD имеет две параллельные стороны и все углы прямые. Это позволяет нам применить теорему Пифагора, которая гласит: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.
В нашем случае, стороны BC и CD являются катетами, а сторона AD является гипотенузой. Мы можем написать следующее уравнение:
BC^2 + CD^2 = AD^2
А теперь посмотрим на значения, которые мы знаем:
- AB = 12
- AD = 17
Мы можем использовать эти значения, чтобы найти длины оставшихся двух сторон:
- Найдем длину стороны BC:
- Найдем длину стороны CD:
BC^2 + CD^2 = AD^2 BC^2 + CD^2 = 17^2 BC^2 + CD^2 = 289 BC^2 + CD^2 = (AB^2 + CD^2) BC^2 = AB^2 BC^2 = 12^2 BC^2 = 144 BC = √144 BC = 12
BC^2 + CD^2 = AD^2 144 + CD^2 = 289 CD^2 = 289 - 144 CD^2 = 145 CD = √145 CD ≈ 12.042
Таким образом, мы нашли, что длина стороны BC равна 12, а длина стороны CD примерно равна 12.042 (с точностью до трех знаков после запятой).
Надеюсь, данное объяснение помогло вам понять, как можно решить данную задачу. Если у вас возникли еще вопросы, не стесняйтесь задавать их!
Решение задачи:
Для того, чтобы решить задачу с прямоугольником ABCD, нам нужно использовать знакомые формулы и применить некоторую логику. Давайте разберемся по порядку.
Из условия задачи мы знаем, что стороны прямоугольника AB и AD равны 12 и 17 соответственно. Давайте обозначим стороны прямоугольника AB и AD как a и b. Теперь у нас есть два уравнения:
a = 12
b = 17
Теперь нам нужно найти площадь прямоугольника ABCD. Площадь прямоугольника равна произведению его сторон, поэтому мы можем использовать формулу:
S = a * b
Подставляя значения сторон прямоугольника AB и AD, мы получаем:
S = 12 * 17 = 204
Таким образом, площадь прямоугольника ABCD равна 204 квадратным единицам. Это наш окончательный ответ.
Шаг 1: Рисуем прямоугольник
Чтобы решить задачу с данным прямоугольником ABCD, первым шагом необходимо его нарисовать. Давайте начнем!
Прямоугольник ABCD имеет стороны AB, AD, BC. По условию задачи, сторона AB равна 12, а сторона AD равна 17. Давайте отметим эти значения на нашем рисунке, чтобы было проще ориентироваться.
Нарисуем прямоугольник ABCD:
| A | B |
| D | C |
Теперь у нас есть базовый рисунок прямоугольника ABCD. Наши стороны AB и AD обозначены на нем длинной 12 и 17 соответственно. Теперь у нас есть визуальное представление прямоугольника и его основных характеристик.
На следующем шаге мы перейдем к решению основной задачи, которая требует вычисления площади этого прямоугольника. Готовы ли вы подсчитать площадь? Отлично! Тогда давайте двигаться дальше!
Шаг 2: Используем теорему Пифагора
Теперь, когда мы знаем длины сторон прямоугольника ABCD (AB = 12 и AD = 17), мы можем использовать теорему Пифагора для вычисления длины третьей стороны BC. Эта теорема гласит, что в прямоугольном треугольнике квадрат гипотенузы (в нашем случае BC) равен сумме квадратов катетов (AB и AD).
Итак, применяя теорему Пифагора к нашей задаче, мы получаем:
BC² = AB² + AD²
Подставляя известные значения, мы можем продолжить вычисления:
BC² = 12² + 17²
BC² = 144 + 289
BC² = 433
Теперь нам нужно найти квадратный корень из значения 433, чтобы получить длину стороны BC.
Может показаться, что это сложная задача, но не стоит паниковать! Здесь мы можем использовать калькулятор или таблицу квадратных корней, чтобы получить точное значение. Попробуй посчитать!
Шаг 3: Извлечение корня
Теперь, когда мы уже знаем площадь прямоугольника, настало время узнать его размеры более точно. Для этого нам понадобится найти корень из значения площади.
Извлекать корень – это, по сути, находить число, при возведении в квадрат которого получается исходное значение. В данном случае у нас есть площадь прямоугольника, которую мы обозначим через S. И чтобы найти стороны прямоугольника, нам нужно извлечь корень из этой площади.
Знаете ли вы, что такое корень из числа? Это величина, которая при возводении в квадрат даёт заданное число. Например, если мы извлечем корень из площади прямоугольника и получим число 25, то это означает, что сторона прямоугольника равна 5.
Итак, чтобы извлечь корень из площади прямоугольника, мы применим важный математический инструмент – квадратный корень. Это будет наша последняя задача на пути к решению. Мы возьмем площадь, которую мы вычислили на предыдущем шаге, и просто найдем квадратный корень этого числа.
Давайте посмотрим, как это выглядит на практике:
Сначала мы возьмем площадь нашего прямоугольника:
S = 204, как мы установили на предыдущем шаге.
Затем мы найдем квадратный корень из этого числа:
√204 ≈ 14.28 (округленно)
Таким образом, длина одной из сторон прямоугольника составляет примерно 14.28.
А что насчет другой стороны?
Для того, чтобы найти вторую сторону, нам просто нужно разделить площадь на длину первой стороны. В нашем случае:
Длина первой стороны = 14.28.
Площадь = 204.
Теперь мы можем использовать формулу:
Длина второй стороны = Площадь / Длина первой стороны.
В нашем случае это будет:
Длина второй стороны = 204 / 14.28 ≈ 14.28 (округленно)
Таким образом, вторая сторона прямоугольника также составляет примерно 14.28.
И вот мы и нашли ответ на поставленную задачу! Размеры прямоугольника ABCD со сторонами AB = 14.28 и AD = 14.28.
Поздравляю! Теперь у вас есть все необходимые знания и навыки для решения задачи с прямоугольником.
Ответ

Задача состояла в определении длин сторон прямоугольника ABCD по известным значениям сторон AB, AD и BC. По условию известно, что сторона AB равна 12, а сторона AD равна 17.
Для определения длины стороны BC необходимо использовать теорему Пифагора, так как стороны AB и AD являются сторонами прямоугольного треугольника. Согласно теореме Пифагора, квадрат длины гипотенузы (BC) равен сумме квадратов длин катетов (AB и AD).
Зная длины сторон AB и AD, можно вычислить длину стороны BC с помощью следующей формулы:
BC = sqrt(AB^2 + AD^2)
Подставляя известные значения в формулу, получаем:
BC = sqrt(12^2 + 17^2)
Подсчитываем значения:
- BC = sqrt(144 + 289)
- BC = sqrt(433)
- BC ≈ 20.81
Таким образом, длина стороны BC примерно равна 20.81.
В итоге, стороны прямоугольника ABCD имеют следующие значения:
- AB = 12
- AD = 17
- BC ≈ 20.81