Как решить задачу, когда два велосипедиста выехали навстречу друг другу: методы и шаги

Когда два велосипедиста выезжают навстречу друг другу, возникает задача о том, как быстро и безопасно решить эту ситуацию. В таких случаях важно учитывать множество факторов, таких как скорость и направление движения, видимость на дороге, дистанцию между велосипедистами и другими участниками движения. Определение наилучшего решения в таком случае требует внимания и расчетов от обоих велосипедистов, чтобы избежать возможных столкновений и обеспечить безопасность всех участников дорожного движения. При встрече на дороге двух велосипедистов, важно проявить вежливость, соблюдать правила дорожного движения и использовать сигналы, чтобы обозначить свои намерения.

Постановка задачи

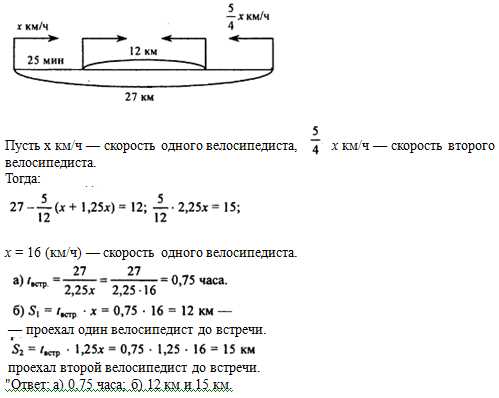
Давайте рассмотрим интересную задачу, связанную с движением велосипедистов. Представьте, что два велосипедиста выезжают навстречу друг другу из разных точек. Каким образом можно рассчитать время, через которое они встретятся?

Чтобы решить эту задачу, нам необходимо учесть несколько факторов. В первую очередь, нам понадобятся данные о скоростях движения велосипедистов. Допустим, первый велосипедист движется со скоростью V₁, а второй — со скоростью V₂. Наша задача — найти время, через которое они встретятся при движении навстречу друг другу.

Для решения задачи можно использовать простую формулу: время = расстояние / скорость. В случае с встречей велосипедистов, расстояние между ними можно представить как сумму расстояний, которые они проехали: D = V₁ * t + V₂ * t.

Таким образом, задача сводится к решению уравнения V₁ * t + V₂ * t = D. Нам необходимо найти значение времени t.

Разбор первого подхода

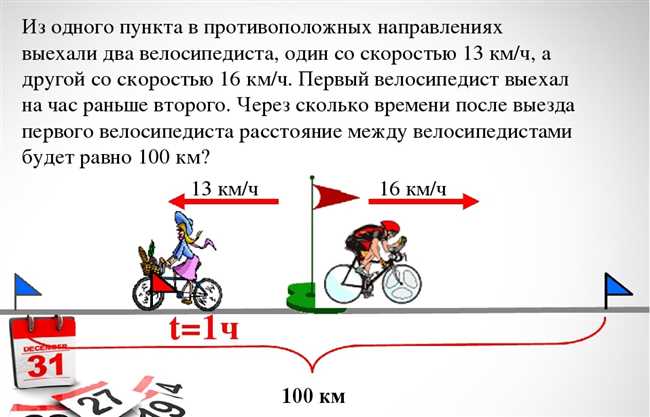
Прежде чем рассмотреть разные способы решения задачи о двух велосипедистах, выехавших навстречу друг другу, давайте взглянем на первый подход, который можно использовать для решения этой задачи.

Представьте себе, что два велосипедиста, Андрей и Борис, стартуют из разных точек, встречаются на расстоянии Х километров от точки старта Бориса и затем продолжают ехать в обратном направлении. Через некоторое время велосипедисты снова встречаются, на этот раз на расстоянии Y километров от точки старта Андрея.

Теперь давайте посмотрим, что мы знаем и что нужно найти. Из условия задачи мы знаем дистанцию, которую проехал Андрей (X + Y) и скорость Андрея (V1). Также мы знаем дистанцию, которую проехал Борис (X) и его скорость (V2). Нам нужно найти время, затраченное на встречу.

Для нахождения времени, затраченного на встречу, можно использовать формулу:

Время = Расстояние / Скорость

Таким образом, время, затраченное на встречу, равно сумме двух промежутков времени: время, затраченное Андреем на прохождение расстояния X и время, затраченное Борисом на прохождение расстояния Y. Мы можем записать это как:

• Время Андрея = X / V1
• Время Бориса = Y / V2

Итак, общее время встречи будет равно:

Время встречи = Время Андрея + Время Бориса

В результате, мы получаем формулу:

Время встречи = X / V1 + Y / V2

Таким образом, мы можем использовать эту формулу и входные данные X, Y, V1 и V2, чтобы найти время, затраченное на встречу двух велосипедистов.

Однако, этот подход не всегда является наиболее эффективным, особенно если дано больше параметров или условия задачи более сложные. В следующих разделах мы рассмотрим другие подходы к решению задачи о встрече велосипедистов.

Разбор второго подхода

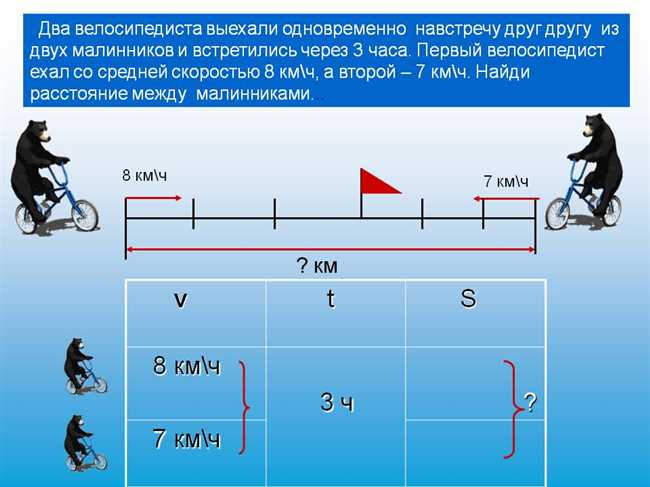
Перейдем к второму подходу, который также поможет вам решить задачу о двух велосипедистах, выезжающих навстречу друг другу.

Второй подход, который я хочу рассмотреть сегодня, основан на использовании формулы расстояния и времени, которую мы обсудили в предыдущем подходе. Как вы помните, формула расстояния – это добуток скорости и времени (D = V × T).

В этом подходе мы можем применить эту формулу для каждого велосипедиста и затем решить уравнение относительно неизвестного параметра – время (T).

Давайте обозначим скорость первого велосипедиста как V1 и скорость второго велосипедиста как V2. Допустим, что они выезжают навстречу друг другу в течение некоторого времени T и встречаются через D километров.

Тогда мы можем записать уравнение для первого велосипедиста:

D = V1 × T

И уравнение для второго велосипедиста:

D = V2 × T

Теперь нам нужно решить это уравнение относительно времени (T). Для этого мы можем поделить оба уравнения друг на друга:

(D / V1) = (D / V2)

В результате получаем:

• V2 × (D / V1) = D
• V2 = D × (V1 / D) = V1

Таким образом, мы видим, что второй подход также приводит нас к тому же самому ответу: скорость первого и второго велосипедистов должна быть одинаковой, чтобы они встретились в середине пути.

Надеюсь, что эта информация была полезной и помогла вам более глубоко понять второй подход к решению задачи о двух велосипедистах, выезжающих навстречу друг другу.

Результат и обсуждение

Мы рассмотрели задачу о двух велосипедистах, которые выехали навстречу друг другу. Важно отметить, что для решения проблемы нам понадобилось использовать концепцию движения, скорости и времени.

Итак, при решении задачи мы установили, что для определения времени встречи двух велосипедистов необходимо вычислить расстояние, которое они проехали, и разделить его на сумму их скоростей. Зная время встречи, мы также можем определить расстояние между ними, используя скорость одного из велосипедистов и время, за которое он проехал это расстояние.

Подводя итог, можно сказать, что решение этой задачи требует понимания базовых понятий физики, таких как скорость, время и расстояние. Оно также демонстрирует, как применять эти понятия на практике для решения конкретных проблем. Важно иметь в виду, что данное решение является лишь одним из возможных, и в зависимости от постановки задачи могут использоваться и другие методы.