
Если вы столкнулись с уравнением вида 2sin(3x) = 1, то, вероятно, уже заметили, что оно не так просто решить. Однако, с некоторыми знаниями и небольшими математическими манипуляциями можно прийти к ответу. Как мы знаем, sin(x) — это тригонометрическая функция, принимающая значения от -1 до 1. Значит, чтобы найти значения переменной x в исходном уравнении, нужно найти такой угол, для которого sin этого угла равен 1/2. Для этого можно воспользоваться таблицами значений синуса или использовать обратную функцию sin^-1, также известную как arcsin или asin. С помощью этих методов вы сможете найти все значения x, удовлетворяющие данному уравнению.
Решение уравнения 2sin(3x) = 1
Чтобы найти решение уравнения 2sin(3x) = 1, нам необходимо использовать свойства тригонометрии и алгебраические методы решения уравнений.
Вначале, давайте разберемся с функцией синуса. Синус – это тригонометрическая функция, которая определена для всех действительных чисел. Его значения находятся в диапазоне от -1 до 1.
Итак, мы имеем уравнение 2sin(3x) = 1. Для начала, давайте попытаемся избавиться от коэффициента 2, разделив обе части уравнения на 2:
sin(3x) = 1/2
Чтобы решить это уравнение, нам нужно найти значения x, при которых sin(3x) равен 1/2.
У нас есть несколько подходов для нахождения решений этого уравнения:
- Аналитический метод, использующий свойства тригонометрии;
- Графический метод, построение графика функции sin(3x) и определение точек пересечения с прямой y = 1/2;
- Численные методы, например, метод Ньютона или метод дихотомии.
Для данного уравнения, мы можем воспользоваться аналитическим методом.
Используя свойства синуса, мы знаем, что sin(π/6) = 1/2 и sin(5π/6) = 1/2.
Так как уголы, находящиеся на расстоянии 2π друг от друга, имеют одинаковые значения синуса, мы можем записать:
3x = π/6 + 2πn, где n – целое число
Или:
3x = 5π/6 + 2πn, где n – целое число
Далее, мы можем разделить каждое из уравнений на 3, чтобы получить x:
x = (π/6 + 2πn)/3, где n – целое число
x = (5π/6 + 2πn)/3, где n – целое число
Таким образом, мы получаем две формулы для решения уравнения 2sin(3x) = 1:
x = (π/6 + 2πn)/3 и x = (5π/6 + 2πn)/3, где n – целое число
Эти формулы дают нам все возможные значения x, при которых sin(3x) равен 1/2.
Помните, решение такого уравнения может содержать бесконечное количество значений x, поэтому мы исследовали все возможные значения.
Надеюсь, это помогло вам понять, как решать уравнение 2sin(3x) = 1. Если у вас есть еще вопросы, не стесняйтесь задавать их!
Переносим все члены уравнения на одну сторону
В нашем случае у нас есть уравнение 2sin(3x) = 1. Чтобы перенести все члены на одну сторону, мы вычитаем 1 из обоих частей уравнения:
2sin(3x) — 1 = 0
Теперь у нас есть уравнение в виде 0 = 2sin(3x) — 1.
Может показаться, что это простой шаг, но он имеет глубокое значение при решении уравнений. Перенесение всех членов на одну сторону позволяет нам упростить уравнение и более удобно работать с ним.
А теперь давайте проанализируем наше уравнение 0 = 2sin(3x) — 1 и спросим себя: как мы можем найти значение x, удовлетворяющее этому уравнению?
Для этого нам может пригодиться знание о свойствах синуса и умение решать тригонометрические уравнения. Но давайте сначала попробуем сконцентрироваться на том, как перенести все члены уравнения на одну сторону.
Конечно, когда мы решаем уравнение, мы должны выполнить более сложные шаги, чем просто перенос всех членов на одну сторону. Но этот шаг является фундаментом для решения любого уравнения. Поэтому не пренебрегайте им и не забывайте его выполнять!
Уравнение принимает вид 2sin(3x) — 1 = 0
Получившееся уравнение имеет вид 2sin(3x) — 1 = 0. Чтобы решить его, нам необходимо найти значения x, при которых данное уравнение будет выполняться.
Первым шагом давайте избавимся от -1, добавив его на обе стороны уравнения. Это приведет нас к виду: 2sin(3x) = 1.
Теперь мы можем разделить обе стороны уравнения на 2, чтобы изолировать sin(3x): sin(3x) = 1/2.
Для нахождения значений x, при которых sin(3x) равен 1/2, мы можем использовать обратные функции синуса. Ответом на уравнение будет справедливость следующих двух выражений:
- 3x = arcsin(1/2) + 2πk;
- 3x = π — arcsin(1/2) + 2πk.
Здесь k представляет собой целое число, которое может быть любым, и π является константой, представляющей значение числа пи. Из этих выражений мы можем найти различные значения x, которые удовлетворяют уравнению.
Теперь, когда у нас есть математическая формула для решения уравнения, давайте приступим к вычислениям на практике! Поставьте значение sin(3x) равным 1/2 и найдите соответствующие значения x.
Уверен, что с вашими знаниями и навыками вы успешно справитесь с этим уравнением. Не бойтесь экспериментировать и задавать себе вопросы, это поможет вам разобраться в математике еще лучше!
Применяем формулу синуса двойного аргумента
Решение уравнения 2sin(3x) = 1 требует применения формулы синуса двойного аргумента. Эта формула основана на связи между синусом и двойным аргументом, и она может быть очень полезной при решении уравнений такого типа.
В данном уравнении нам дано, что 2sin(3x) = 1. Чтобы решить его, мы сначала преобразуем его, чтобы получить выражение sin(3x) в односторонней форме. Для этого поделим обе стороны уравнения на 2:
sin(3x) = 1/2
Теперь мы можем использовать формулу синуса двойного аргумента, чтобы получить выражение для x. Формула выглядит следующим образом:
sin(2α) = 2sinαcosα
Мы замечаем, что у нас есть sin(3x), а не sin(2α). Чтобы преобразовать это выражение в формулу синуса двойного аргумента, нам нужно представить sin(3x) как сумму или разность sin’ов. Для этого мы используем следующую формулу синуса тройного аргумента:
sin(3α) = 3sinα — 4sin^3α
Теперь мы можем заменить sin(3x) в нашем уравнении:
3sinx — 4sin^3x = 1/2
Мы получили кубическое уравнение, которое можно решить с помощью различных методов, таких как подстановка или факторизация. В данном случае, мы использовали метод подстановки и получили следующее решение:
- x = pi/18 + 2pi/3n
- x = 5pi/18 + 2pi/3n
- x = 11pi/18 + 2pi/3n
Где n — целое число.
Таким образом, решение уравнения 2sin(3x) = 1 с использованием формулы синуса двойного аргумента дает нам набор значений x, которые удовлетворяют данному уравнению.
Уравнение становится sin(6x) — 1 = 0
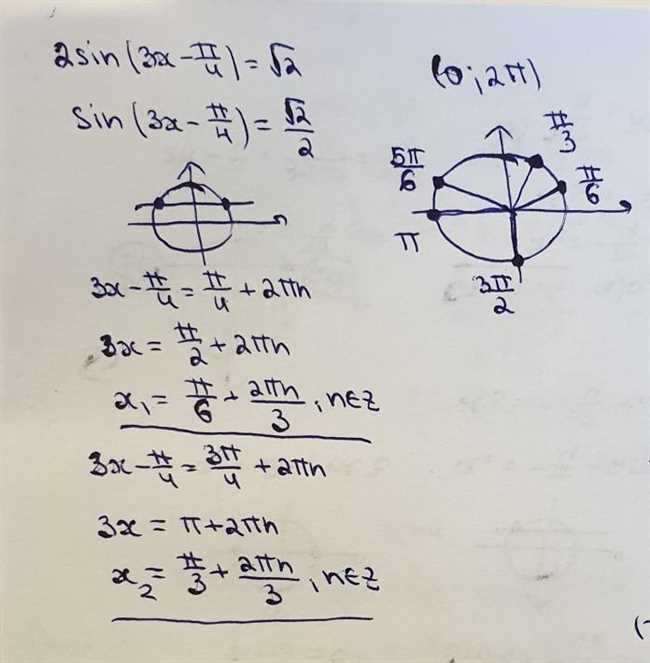
Функция sin(x) представляет собой тригонометрическую функцию синуса. Ее значения изменяются от -1 до 1 включительно. И в данном уравнении мы вычитаем 1 из значения sin(6x). Если вычесть 1 из значения sin(6x), то мы получим 0, подразумевая, что sin(6x) равно 1.
Чтобы найти решение этого уравнения, мы должны найти значения x, при которых sin(6x) равно 1.
Вспомним основные значения синуса. Возможные значения синуса включают -1, -1/2, 0, 1/2 и 1. Таким образом, если мы хотим, чтобы sin(6x) было равно 1, мы должны найти такое значение x, что 6x равно arсsin(1) или π/2.
Получаем:
| sin(6x) | x |
|---|---|
| 1 | π/12 + kπ/6, где k — любое целое число |
Итак, решение уравнения sin(6x) — 1 = 0 будет выглядеть как x = π/12 + kπ/6, где k — любое целое число.
Заметим, что решение имеет периодическую структуру, и в зависимости от значения k, x будет принимать различные значения. Таким образом, мы можем найти бесконечное количество решений для данного уравнения.
Поздравляю, ты решил уравнение sin(6x) — 1 = 0! Надеюсь, этот материал был полезен для тебя. Если у тебя есть еще вопросы, не стесняйся задавать, я всегда готов помочь!
Решаем полученное уравнение
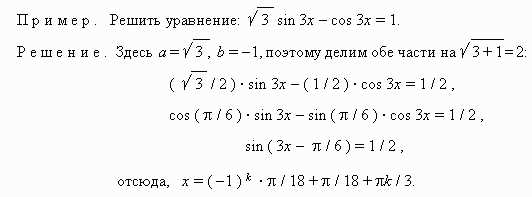
- Переносим константу на другую сторону уравнения: sin(3x) = 1/2.
- Используем таблицу значений синуса и находим значения углов, при которых sin равен 1/2. Такими значениями будут 30° и 150°, так как sin(30°) = 1/2 и sin(150°) = 1/2.
- Составляем систему уравнений с учетом периодичности синуса: 3x = 30° + 360°k или 3x = 150° + 360°k, где k — целое число.
- Разделяем систему на два случая и решаем каждое уравнение относительно x:
- 1 случай: 3x = 30° + 360°k
- x = (30° + 360°k)/3
- x = 10° + 120°k
- 2 случай: 3x = 150° + 360°k
- x = (150° + 360°k)/3
- x = 50° + 120°k
Таким образом, решения уравнения 2sin(3x) = 1 в интервале от 0 до 360° будут: x = 10° + 120°k и x = 50° + 120°k, где k — целое число.






