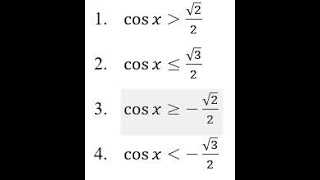
Как решить неравенство Cosx>0: подробный гайд и примеры
Если вам нужно решить неравенство Cosx>0, то вы находитесь в правильном месте. В этом подробном гайде мы рассмотрим, как точно решить данное неравенство. Чтобы понять, когда косинус x является положительным, вам нужно знать основные свойства косинуса и его график. Мы проведем вас через каждый шаг решения, объясняя его подробно и предоставляя примеры. Это поможет вам понять концепцию и справиться с задачами самостоятельно. Примеры помогут вам увидеть, как применять наши рекомендации на практике. Готовы разобраться с неравенством Cosx>0? Тогда давайте начнем!
Определение косинуса
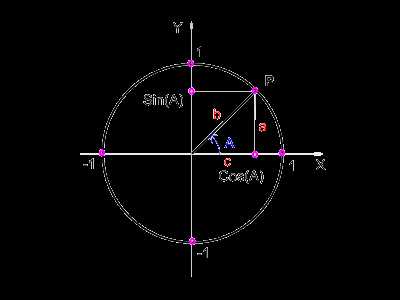
Когда мы говорим о косинусе угла, мы обычно имеем в виду угол внутри прямоугольного треугольника, составленного по координатной плоскости. В этом случае, косинус угла равен отношению координаты x точки на окружности, на которой лежит конец стороны в прямоугольном треугольнике, к радиусу этой окружности.
Косинус угла обозначается с помощью функции «cos», и его значение может быть в диапазоне от -1 до 1.
Значение косинуса зависит от величины угла, для которого он вычисляется. Когда угол равен 0, косинус равен 1, что означает, что прилежащий катет равен гипотенузе. Когда угол равен 90 градусов, косинус равен 0, что означает, что прилежащий катет равен 0.
Косинус также является периодической функцией, с периодом 2π или 360 градусов. Это означает, что косинус для угла θ и для угла θ + 2π (или θ + 360 градусов) будет иметь одинаковое значение.
Косинус имеет множество приложений в математике, физике, инженерии и других науках. Например, он используется для определения расстояния искажения изображения в компьютерной графике, моделирования колебаний и волновых процессов, и даже для анализа музыкальных звуков.
Изучение косинуса и его свойств позволяет нам более глубоко понять и анализировать различные физические и математические явления, и применять этот знания в нашей повседневной жизни.
Первый шаг: Разбиение интервала
Чтобы начать разбиение интервала, мы должны сначала определить все точки, в которых функция cos(x) равна нулю. Для этого мы решаем уравнение cos(x) = 0.
Уравнение cos(x) = 0 имеет бесконечно много решений, которые соответствуют периодическости функции cos(x). Одно из таких решений — это x = π/2.
Если мы построим график функции cos(x), то увидим, что она пересекает ось абсцисс в точках x = π/2 + kπ, где k — целое число. То есть, можно сказать, что все значения x, которые можно представить в виде π/2 + kπ, являются решениями уравнения cos(x) = 0.
Теперь, когда мы знаем точки, в которых функция cos(x) равна нулю, мы можем разбить интервал на подынтервалы. Один из примеров разбиения для уравнения cos(x) > 0:
| Подынтервал | Условие | Решение |
|---|---|---|
| x < π/2 | cos(x) > 0 | Решение: 0 < x < π/2 |
| π/2 < x < 3π/2 | cos(x) < 0 | Решение: Нет решений |
| x > 3π/2 | cos(x) > 0 | Решение: 3π/2 < x < 2π |
Таким образом, мы получили разбиение интервала для неравенства cos(x) > 0. Мы разделили интервал на три подынтервала и определили, в каких из них функция cos(x) положительна.
Теперь, когда у нас есть подынтервалы, в которых функция cos(x) положительна, мы можем перейти ко второму шагу решения неравенства. (На следующем шаге, мы будем исследовать знак функции cos(x) в каждом подынтервале и определить решение неравенства.)
Второй шаг: Поиск значений косинуса
Чтобы найти такие значения, необходимо обратиться к графику косинуса. Нарисуйте график косинуса на координатной плоскости и обратите внимание на точки, где косинус положителен.
На графике косинуса можно видеть, что функция принимает положительные значения между точками пересечения с осью OX. То есть, когда аргумент находится в одном из следующих интервалов:
- между 0 и π,
- между 2π и 3π,
- между 4π и 5π,
- и так далее.
В этих интервалах косинус будет положителен, и, следовательно, выполняется неравенство Cosx > 0.
Теперь подумайте о том, как можно записать эти интервалы с использованием математической нотации. Пригодятся также знания о периодичности косинуса, то есть о его значениях через каждый полный оборот.
Попробуйте сформулировать ответ самостоятельно перед тем, как продолжите чтение.
Готовы узнать правильный ответ?
Для записи интервалов, в которых выполняется Cosx > 0, используется следующая нотация:
- (2nπ, (2n + 1)π), где n принадлежит к множеству целых чисел.
Эта запись означает, что значения аргумента находятся между 0 и π, между 2π и 3π, между 4π и 5π и так далее. Во всех этих интервалах косинус будет положителен и выполняется неравенство Cosx > 0.
Теперь вы знаете, как найти значения косинуса, удовлетворяющие неравенству Cosx > 0. Это очень полезное знание, которое может быть применено в различных математических задачах. Хотите попробовать решить некоторые примеры сами?
Третий шаг: Построение графика
Теперь, когда мы определили диапазон значений x, удовлетворяющих неравенству Cosx > 0, настало время построить график функции y = Cosx и определить интервалы, на которых она положительна.
График функции Cosx представляет собой гладкую кривую с периодом 2π. При этом, на интервалах (π/2 + 2nπ, 3π/2 + 2nπ), где n — любое целое число, значение Cosx будет положительным. Это связано с тем, что на этих интервалах косинусная функция принимает положительное значение, а ноль не включен в положительные числа.
Чтобы наглядно представить график функции Cosx, мы можем использовать таблицу значений или рисовать его на графическом калькуляторе. Но самым простым и наглядным способом является построение графика на координатной плоскости, где ось X будет представлять значения x, а ось Y — значения Cosx.
Теперь, зная интервалы, на которых Cosx положителен, мы можем отметить эти интервалы на графике функции. Для этого мы выделим на координатной плоскости отрезки, соответствующие данным интервалам, и будем рисовать функцию на этих отрезках. На остальных интервалах, где Cosx отрицателен или равен нулю, график функции будет находиться ниже оси X или пересекать ее.
Например, если мы рассматриваем интервал (0, 2π), то график Cosx будет положителным на интервалах (π/2, 3π/2) и (5π/2, 7π/2), так как на этих интервалах Cosx больше нуля. Обратите внимание, что нули косинусной функции находятся в точках, где график функции пересекает ось X.
Заключение
В данной статье мы рассмотрели способы решения неравенства Cosx>0. Во-первых, мы выяснили, что неравенство выполняется в тех областях, где косинус функции положителен. Во-вторых, мы разобрали несколько примеров решения подобных неравенств.
При решении неравенств с косинусом нужно ориентироваться на график функции, который имеет периодический характер и изменяется от -1 до 1. Таким образом, для выполнения условия Cosx>0 необходимо найти все области, где функция находится выше нуля.
- Пример 1: Если рассматривать интервал от 0 до 2π, то Cosx>0 в областях между 0 и π, а также между 2π и 3π.
- Пример 2: На интервале от -π/2 до π/2 неравенство выполнено для всех значений, кроме самой точки 0.
Таким образом, решениями неравенства Cosx>0 могут быть интервалы (0, π) и (2π, 3π), а также все значения x, кроме x=0, на интервале (-π/2, π/2).






