Как решить дискриминант с одним корнем? Узнайте подробный гайд и примеры

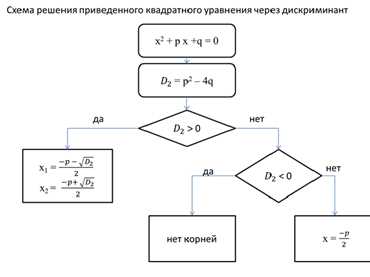
Определение дискриминанта

Если дискриминант больше нуля (D > 0), то квадратное уравнение имеет два различных корня — один положительный и один отрицательный. Например, уравнение x² — 5x + 6 = 0 имеет корни x₁ = 2 и x₂ = 3.

Если дискриминант равен нулю (D = 0), то квадратное уравнение имеет один корень, который является вещественным и совпадает с основным значением. Например, уравнение x² — 6x + 9 = 0 имеет корень x = 3.

Если дискриминант меньше нуля (D < 0), то квадратное уравнение не имеет вещественных корней, а имеет только комплексные корни. В этом случае уравнение может быть решено с помощью мнимых чисел. Например, уравнение x² + 5x + 9 = 0 не имеет вещественных корней.

Знание дискриминанта позволяет анализировать и понимать свойства квадратных уравнений, а также решать их с помощью различных методов. Он является важным инструментом для решения математических задач, требующих работы с квадратными уравнениями.

Краткий обзор дискриминанта с одним корнем

Один корень дискриминанта означает, что квадратное уравнение имеет только один корень, или другими словами, уравнение имеет единственное решение.

Как найти дискриминант с одним корнем? Для этого нам необходимо вычислить значение дискриминанта по формуле b^2 — 4ac и проверить, равен ли он нулю. Если дискриминант равен нулю, то уравнение имеет только один корень. Это означает, что график квадратного уравнения касается оси x в одной точке.

Одним из примеров таких уравнений может быть x^2 + 4x + 4 = 0. В этом примере a = 1, b = 4, c = 4. Вычислим дискриминант: (4)^2 — 4(1)(4) = 16 — 16 = 0. Таким образом, уравнение имеет только один корень — x = -2.

Дискриминант с одним корнем указывает на специальный случай квадратного уравнения, когда оно имеет единственное решение. Это может происходить в различных ситуациях, и важно уметь распознавать и обрабатывать такие случаи при решении задач.

Шаги для решения дискриминанта с одним корнем

Решение квадратных уравнений с одним корнем может быть довольно простым и легким процессом. Когда дискриминант, то есть значение под корнем в квадратном уравнении, равен нулю, это означает, что уравнение имеет только один корень. Для решения таких уравнений можно использовать следующие шаги:

1. Найдите значение дискриминанта (D) в квадратном уравнении $ax^2 + bx + c = 0$, где а, b и с — константы. Дискриминант вычисляется по формуле $D = b^2 — 4ac$.
2. Проверьте, равен ли дискриминант нулю. Если да, то уравнение имеет только один корень.
3. Найдите значение корня, используя формулу $x = -\frac{b}{2a}$.
4. Проверьте правильность решения, подставив найденное значение x в исходное уравнение и проверив, равно ли оно нулю.

Давайте рассмотрим пример, чтобы лучше понять шаги для решения дискриминанта с одним корнем.

Пример:

Решите уравнение $3x^2 — 6x + 3 = 0$.

Шаг 1: Вычислим дискриминант.

Здесь a = 3, b = -6 и c = 3.

$D = (-6)^2 — 4(3)(3) = 36 — 36 = 0$

Шаг 2: Проверим, равен ли дискриминант нулю.

Да, $D = 0$, поэтому уравнение имеет только один корень.

Шаг 3: Найдем значение корня, используя формулу.

$x = -\frac{-6}{2(3)} = \frac{-6}{6} = -1$

Шаг 4: Проверим правильность решения, подставив найденное значение x в исходное уравнение.

$3(-1)^2 — 6(-1) + 3 = 3 + 6 + 3 = 12

eq 0$

Уравнение не равно нулю, поэтому решение неправильное.

Если ваше решение не приводит к правильному ответу, пройдите все шаги еще раз, убедившись в правильности вычислений и подстановок. Возможно, вы допустили ошибку на одном из шагов. В таком случае, решите уравнение заново, чтобы найти правильное значение корня.

Решение дискриминанта с одним корнем может быть простым и быстрым процессом, подразумевающим всего лишь несколько шагов. Выполняя эти шаги с тщательностью и точностью, вы сможете легко решать уравнения с одним корнем и получать правильные ответы. Успехов вам!

Примеры решения дискриминанта с одним корнем

Пример 1:

Решим уравнение x² + 6x + 9 = 0. Найдем дискриминант:

Дискриминант = b² — 4ac, где a, b и c – коэффициенты уравнения.

В данном уравнении a = 1, b = 6, c = 9.

Подставляем значения в формулу дискриминанта:

D = (6)² — 4(1)(9) = 36 — 36 = 0

Таким образом, дискриминант равен нулю.

Это означает, что у уравнения есть только один корень.

Чтобы найти этот корень, можно использовать стандартную формулу: x = -b / (2a).

Подставляем значения в формулу: x = -6 / (2 * 1) = -6 / 2 = -3.

Таким образом, решением уравнения является x = -3.

Пример 2:

Решим уравнение 2x² — x — 1 = 0. Найдем дискриминант:

D = (-1)² — 4(2)(-1) = 1 + 8 = 9

Дискриминант равен 9, что означает, что у уравнения есть два различных корня.

Однако, если мы получаем дискриминант равный нулю, у нас будет только один корень.

Вернемся к нашему уравнению.

Таким образом, решением уравнения является x = -b / (2a), или x = 1 / (4).

Мы получили только один корень.

Пример 3:

Решим уравнение x² + 4x + 4 = 0. Найдем дискриминант:

D = (4)² — 4(1)(4) = 16 — 16 = 0

Дискриминант равен нулю, поэтому у уравнения есть только один корень.

Применяем формулу для нахождения корня: x = -b / (2a).

Подставляем значения в формулу: x = -4 / (2 * 1) = -4 / 2 = -2.

Таким образом, решением уравнения является x = -2.

Это были несколько примеров решения дискриминанта с одним корнем. Определять количество корней уравнения может быть полезным при решении различных математических и физических задач. Успехов в изучении математики!

Важные советы и рекомендации

В решении дискриминанта, когда он имеет только один корень, существует несколько важных советов и рекомендаций, которые помогут вам справиться с такими уравнениями:

• Тщательно проверьте коэффициенты уравнения: Перед тем, как приступить к решению уравнения, убедитесь, что все коэффициенты правильно записаны и учитываются соответствующим образом.
• Используйте подходящую формулу дискриминанта: В зависимости от типа уравнения, существуют различные формулы для вычисления дискриминанта. Убедитесь, что вы правильно выбрали формулу для решения конкретного уравнения.
• Тщательно проверьте свои вычисления: Ошибки в вычислениях могут привести к неправильному результату. Всегда проверяйте свои вычисления несколько раз, чтобы убедиться в их точности.
• Обратите внимание на отрицательные значения дискриминанта: Если дискриминант отрицательный, уравнение не имеет действительных корней. Это может быть полезной информацией при решении задачи.
• Используйте графики для визуализации уравнения: Создание графика уравнения может помочь визуализировать его и наглядно представить, как он пересекает оси координат и какой тип корней у него может быть.

Используя эти советы и рекомендации, вы сможете более эффективно решать уравнения с одним корнем дискриминанта.