Когда мы решаем задачи с касательной прямой y=4x+11 к графику, нам нужно определить точку касания и найти точку, в которой касательная пересекает ось ординат. Для этого нам потребуется использовать знания о производной функции. Производная функции задает наклон касательной прямой к графику в каждой точке. Если производная равна 4, то это означает, что наклон касательной прямой равен 4 и уравнение прямой будет выглядеть как y=4x+b, где b — это точка, в которой касательная пересекает ось ординат. Определение точки касания возможно приравнением уравнения исходной функции к уравнению касательной прямой и решением этой системы уравнений.
Постройте график функции y=4x+11
Начнем с построения этой точки. Расположим ее на вертикальной оси ординат (y-оси) в 11 единицах от начала координат. После этого на графике проведем прямую, идущую через эту точку и с угловым коэффициентом 4.
Вооружившись этой информацией, давайте начнем строительство графика:
| x | y = 4x + 11 |
|---|---|
| 0 | 11 |
| 1 | 15 |
| 2 | 19 |
| 3 | 23 |
| 4 | 27 |
Построим точку (0, 11) на графике. Это будет наше начальное положение для прямой. Затем соединим эту точку с другими точками, распределенными вдоль оси абсцисс (x-оси) с постоянным шагом. Смотрим на таблицу, например, при значениях x=1, x=2, x=3 и x=4, соответствующие значения y будут составлять 15, 19, 23 и 27 соответственно.
Проведем прямую, проходящую через все эти точки, и мы получим график функции y=4x+11.
Найдите точку касания
Чтобы найти точку касания, мы должны найти значения координат x и y, которые удовлетворяют одновременно уравнению касательной прямой и уравнению графика функции.
Для примера возьмем уравнение касательной прямой y=4x+11. Таким образом, мы имеем уравнение вида y=ax+b, где a — коэффициент при x, а b — свободный член.
Предположим, что у нас есть график функции y=f(x), и мы хотим найти точку касания этой функции с прямой y=4x+11. Для этого мы должны приравнять уравнения:
f(x) = 4x + 11
Теперь нам нужно решить это уравнение для x, чтобы найти значение x-координаты точки касания.
Пример:
Рассмотрим функцию y=x^2 и прямую y=4x+11. Найдем точку их пересечения.
- Подставим уравнение прямой в уравнение функции:
- x^2 = 4x + 11
- Перенесем все члены уравнения в одну сторону:
- x^2 — 4x — 11 = 0
- Применим квадратное уравнение:
- D = b^2 — 4ac = (-4)^2 — 4*1*(-11) = 16+44 = 60
- Так как дискриминант больше нуля, у уравнения есть два корня:
- x1 = (4 + √60) / 2 = (4 + √15√4) / 2 = (4 + 2√15) / 2 = 2 + √15
- x2 = (4 — √60) / 2 = (4 — √15√4) / 2 = (4 — 2√15) / 2 = 2 — √15
Теперь у нас есть две возможные x-координаты точек пересечения прямой и функции. Чтобы найти соответствующие y-координаты, мы просто подставим найденные значения x в уравнение касательной прямой.
Для нашего примера мы получим:
x1 = 2 + √15, y1 = 4(2 + √15) + 11 = 8 + 4√15 + 11 = 19 + 4√15
x2 = 2 — √15, y2 = 4(2 — √15) + 11 = 8 — 4√15 + 11 = 19 — 4√15
Таким образом, мы получили две точки пересечения прямой y=4x+11 и функции y=x^2 — (2 + √15, 19 + 4√15) и (2 — √15, 19 — 4√15).
Определение угла наклона касательной прямой
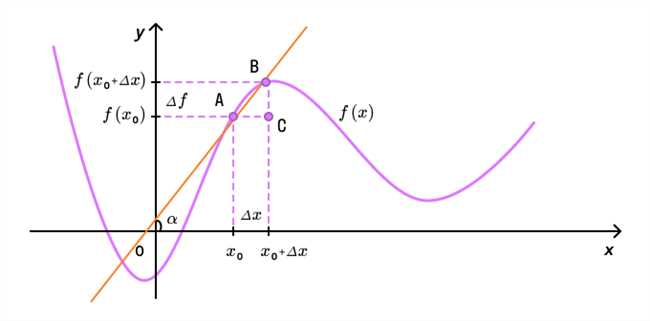
Угол наклона касательной прямой определяется комплексными и прямыми методами. Рассмотрим каждый из них.
Комплексный метод
Для определения угла наклона касательной прямой с использованием комплексного метода необходимо применить понятие производной функции в точке касания прямой с графиком.
Допустим, у нас имеется функция y = f(x), а прямая касается графика функции в точке с координатами (a, f(a)). Тогда производная функции в этой точке может быть представлена следующим образом:
f'(a) = lim(h→0) [f(a+h) — f(a)] / h
Угол наклона касательной прямой равен тангенсу угла наклона прямой, проведенной через начало координат и точку касания. Тангенс угла наклона можно выразить через производную функции:
tan(α) = f'(a)
Где α — угол наклона касательной прямой в радианах.
Прямой метод
Альтернативный способ определения угла наклона касательной прямой — использование прямого метода. Для этого достаточно следовать простым шагам:
- Найдите координаты двух точек, через которые проходит касательная прямая.
- Используя найденные координаты, вычислите разность координат по оси x и оси y.
- Вычислите тангенс угла наклона с помощью формулы: tan(α) = (y2 — y1) / (x2 — x1).
Теперь вы знаете, как определить угол наклона касательной прямой с помощью комплексного и прямого методов. Отличная работа! Теперь, когда вы понимаете, как решать такие задачи, вы можете применять свои знания на практике и успешно справляться с математическими вызовами.
Решите задачу, используя уравнение касательной прямой

Для решения задачи, связанной с графиком функции, и точкой на этом графике, мы можем использовать уравнение касательной прямой. Уравнение касательной прямой позволяет нам найти уравнение прямой, которая касается графика функции в заданной точке, в данном случае у нас имеется график функции y=4x+11.
Для того чтобы найти уравнение касательной прямой, нам необходимо знать координаты заданной точки на графике функции. В данном случае пусть заданная точка имеет координаты (x, y).
Используя формулу для нахождения уравнения касательной прямой, которая выглядит следующим образом: y — y1 = m(x — x1), где (x1, y1) — координаты заданной точки, а m — угловой коэффициент графика функции.
Подставляем в формулу известные значения и решаем уравнение относительно y, чтобы получить уравнение касательной прямой, которое будет иметь вид y = mx + (y1 — mx1).
Таким образом, используя уравнение касательной прямой, мы можем решать задачи, связанные с графиками функций и точками на этих графиках.