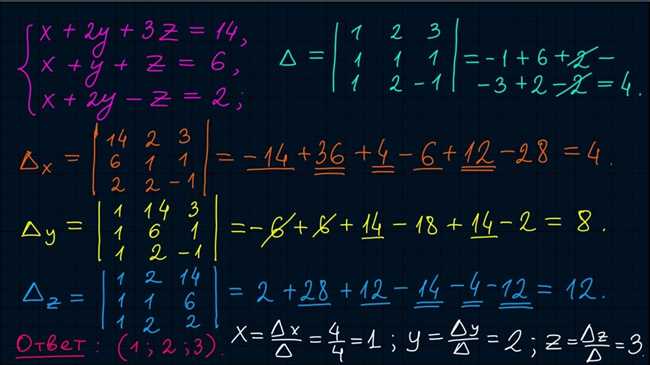
Когда мы сталкиваемся с уравнениями с тремя неизвестными, нам требуется использовать основные методы для их решения. Такие уравнения являются системами линейных уравнений, в которых три переменные связаны между собой несколькими уравнениями. Для решения таких систем можно использовать методы подстановки, методы сложения и вычитания, а также метод Крамера. Метод подстановки заключается в решении одного уравнения относительно одной переменной и подстановке его значения в другие уравнения. Метод сложения и вычитания основан на складывании или вычитании уравнений, чтобы получить новые уравнения без одной переменной. Метод Крамера использует определители, чтобы найти значения переменных. Рассмотрим примеры использования этих методов для решения уравнений с тремя неизвестными.
Метод подстановки: упрощение уравнений с тремя неизвестными
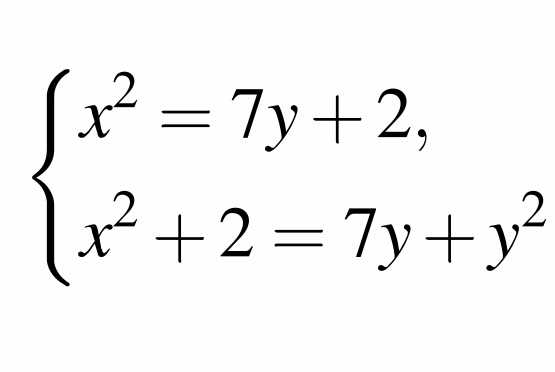
Допустим, у нас есть система уравнений:
ах + by + cz = d
ex + fy + gz = h
ix + jy + kz = l
Для начала выберем одно уравнение и найдем в нем наиболее удобную переменную для подстановки. Например, возьмем первое уравнение и найдем х:
х = (d — by — cz) / a
Теперь подставим полученное выражение для х в остальные два уравнения:
e((d — by — cz) / a) + fy + gz = h
i((d — by — cz) / a) + jy + kz = l
После упрощения уравнений, мы получим систему уравнений с двумя неизвестными:
Ay + Bz = C
Dy + Ez = F
Далее мы можем использовать различные методы решения уравнений с двумя неизвестными, например метод Гаусса или метод Крамера, для нахождения значений неизвестных переменных.
Метод подстановки является достаточно простым и эффективным способом решения уравнений с тремя неизвестными. Он позволяет постепенно упрощать исходные уравнения до системы с двумя неизвестными, что делает процесс решения более понятным и удобным.
Например, рассмотрим систему уравнений:
2x + 3y + z = 10
3x — 2y + 2z = 4
x + y + 3z = 8
Выберем первое уравнение и найдем х:
х = (10 — 3y — z) / 2
Подставим полученное выражение во второе и третье уравнение:
3((10 — 3y — z) / 2) — 2y + 2z = 4
((10 — 3y — z) / 2) + y + 3z = 8
После упрощения получим следующую систему уравнений:
-2y — 5z = -8
2y + 5z = 2
Используя метод Крамера или любой другой метод решения уравнений с двумя неизвестными, мы можем найти значения y и z.
Таким образом, метод подстановки является одним из инструментов, который поможет вам решить уравнения с тремя неизвестными. Этот метод позволяет пошагово упрощать систему уравнений до более простой системы с двумя неизвестными, что делает процесс решения более понятным и удобным.
Метод исключения
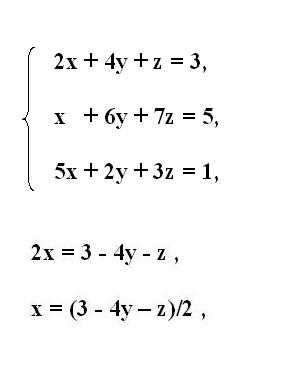
Давайте рассмотрим пример. У нас есть система уравнений:
-
Уравнение 1: 2x + 3y — z = 10
-
Уравнение 2: 3x — 2y + 4z = 5
-
Уравнение 3: x + 2y — 3z = -3
Для начала выберем одну из переменных, скажем, x. Чтобы исключить x, нужно решить первые два уравнения системы относительно x.
Решим первые два уравнения. Для этого умножим первое уравнение на 3, а второе уравнение на 2, чтобы коэффициенты при x были одинаковыми:
-
Уравнение 1 умноженное на 3: 6x + 9y — 3z = 30
-
Уравнение 2 умноженное на 2: 6x — 4y + 8z = 10
Теперь вычтем второе уравнение из первого:
-
(6x + 9y — 3z) — (6x — 4y + 8z) = 30 — 10
-
13y — 11z = 20
В итоге, мы получили новое уравнение, в котором нет переменной x.
Теперь решим новую систему:
-
Уравнение 3: x + 2y — 3z = -3
-
Уравнение 4: 13y — 11z = 20
Для этого умножим первое уравнение на 13 и второе уравнение на -1, чтобы коэффициенты при y были одинаковыми:
-
Уравнение 3 умноженное на 13: 13x + 26y — 39z = -39
-
Уравнение 4 умноженное на -1: -13x + 11z = -20
Теперь сложим эти уравнения:
-
(13x + 26y — 39z) + (-13x + 11z) = -39 — 20
-
37y — 28z = -59
В результате мы получили новое уравнение, в котором нет переменных x и y.
Теперь можем решить это новое уравнение:
-
37y — 28z = -59
В методе исключения мы последовательно решаем подсистемы, исключая переменные, чтобы в конечном итоге получить одно уравнение с одной неизвестной.
В данном примере мы исключили переменные x и y, получив уравнение с двумя неизвестными: 37y — 28z = -59. Далее, для нахождения конкретных значений y и z, нужно использовать другой метод, например, подстановку или метод Гаусса.
Метод исключения является мощным инструментом для решения систем уравнений с тремя неизвестными. Он помогает упростить систему, исключив одну из переменных, и перейти к решению системы с меньшим числом неизвестных.
Метод замены переменных
Почему нам нужен метод замены переменных? Дело в том, что в некоторых сложных уравнениях с тремя неизвестными не всегда возможно найти тривиальное решение с помощью арифметических операций. Метод замены переменных позволяет нам обойти эту проблему и найти неизвестные, избегая сложных числовых вычислений.
Как же работает этот метод? Представьте себе, что у вас есть уравнение с тремя неизвестными:
ax + by + cz = d
Чтобы упростить это уравнение, мы можем заменить переменные так, чтобы они стали более удобными для дальнейших вычислений. Например, если у нас есть уравнение, где x, y и z являются координатами точек в трехмерном пространстве, мы можем заменить их следующим образом:
x = u — v
y = u + v
z = w
Теперь, подставив эти замены в исходное уравнение, мы получим новое уравнение с переменными u, v и w:
a(u — v) + b(u + v) + cw = d
Далее мы можем упростить это уравнение, раскрыв скобки и объединив подобные члены, чтобы получить конечное уравнение, содержащее только переменные u, v и w.
Теперь, почему это полезно? Преимущество метода замены переменных заключается в том, что в новых переменных уравнение может стать более простым и симметричным. Это может сделать задачу решения уравнения более понятной и легче решаемой.
Итак, метод замены переменных — это мощный инструмент для решения уравнений с тремя неизвестными. Он позволяет нам упростить уравнения и найти значения неизвестных, избегая сложных итераций и вычислений.
Пример использования метода замены переменных:
Предположим, у нас есть следующее уравнение:
2x + 3y — z = 10
x — 2y + 3z = -4
3x — y + 2z = 7
Мы можем заменить переменные следующим образом:
x = u — v
y = u + v
z = w
Подставляя эти замены в исходные уравнения, мы получим:
2(u — v) + 3(u + v) — w = 10
(u — v) — 2(u + v) + 3w = -4
3(u — v) — (u + v) + 2w = 7
Далее мы можем раскрыть скобки и объединить подобные члены, чтобы упростить уравнения:
5u + w = 10
-3u + 3v + 3w = -4
2u — 3v + 5w = 7
Теперь мы получили новую систему уравнений, которую можно решить, используя любой из других методов, например, метод гаусса или метод Крамера. Найдя значения u,v и w, мы можем заменить их обратно в исходные замены, чтобы определить значения x, y и z.
Итак, вот как работает метод замены переменных. Попробуйте использовать этот метод при решении уравнений с тремя неизвестными, и у вас откроется новый взгляд на решение сложных математических задач!
Примеры решения уравнений с тремя неизвестными
В данной статье мы рассмотрели основные методы решения уравнений с тремя неизвестными. Приведем несколько примеров, чтобы продемонстрировать эти методы в действии.
Пример 1:
Рассмотрим систему уравнений:
2x + 3y + z = 7
x + y — z = 3
3x — y + 2z = 1
Метод Гаусса позволяет привести систему к ступенчатому виду и найти значения неизвестных. Применяя метод, получаем:
| x | y | z |
| 1 | 0 | -1 |
| 0 | -3 | 5 |
| 0 | 0 | 4 |
Таким образом, значения неизвестных равны: x = 1, y = -3, z = 4.
Пример 2:
Рассмотрим систему уравнений:
x + y + z = 6
x + 2y + 3z = 14
2x + 4y + 6z = 28
Метод подстановки позволяет выразить одну из переменных через остальные и подставить это выражение в остальные уравнения. Применяя метод, получаем:
x = 2, y = 1, z = 3
Таким образом, значения неизвестных равны: x = 2, y = 1, z = 3.
Примеры решения систем уравнений с тремя неизвестными позволяют наглядно представить применение различных методов и упростить процесс решения. Знание основных методов позволяет успешно решать подобные задачи в различных областях науки и техники.






