Как разделить окружность на восемь равных частей подробная инструкция

Как разделить окружность на восемь равных частей? Это достаточно просто, и я расскажу вам подробную инструкцию. Во-первых, нужно провести две пересекающиеся окружности, так чтобы они имели общий центр и радиус. Затем, проведите линию от центра каждой окружности до точки пересечения. Получившиеся линии разделят окружность на четыре части. После этого, проведите линию из центра каждой окружности до точки пересечения противоположной окружности. Теперь окружность разделена на восемь равных частей. Этот метод основан на геометрических принципах и может быть использован без специального оборудования. Так что, если вам нужно разделить окружность на восемь равных частей, просто следуйте этой инструкции.

Окружность: основные понятия

Важно отметить, что вокруг окружности есть два основных понятия: диаметр и окружность. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр. Диаметр обозначается символом «d» или «D» и является удвоенным радиусом: d=2r.

Окружность также характеризуется длиной окружности, которая вычисляется по формуле: L=2πr, где «π» (пи) – математическая константа, приближенное значение которой равно 3,14159.

Понимание основных понятий окружности важно для решения различных геометрических задач. Например, зная радиус или диаметр окружности, мы можем вычислить её длину или площадь.

Интересно знать, что окружность является одной из наиболее важных геометрических фигур и применяется во многих областях науки и практической деятельности. Она используется в физике для описания движения тела по окружности, в архитектуре для создания круглых форм, в математике для изучения геометрических проблем, а также в рисовании и дизайне для создания красивых и симметричных изображений.

Что такое окружность?

Окружность является одной из самых фундаментальных и важных геометрических фигур. Она широко используется в различных областях науки, инженерии и ежедневной жизни.

Важными характеристиками окружности являются ее диаметр, который является наибольшим отрезком, соединяющим две противоположные точки на окружности, и длина окружности, которая вычисляется по формуле C = 2πR, где R — радиус окружности.

Окружности могут иметь различные свойства и использоваться для решения различных задач. Они используются в геометрии для изучения свойств и взаимоотношений между различными фигурами, а в приложениях, например, в архитектуре и строительстве, они используются для создания круглых форм и поверхностей.

Теперь, когда мы знаем, что такое окружность, давайте поговорим о том, как ее можно разделить на восемь равных частей. Это интригующая задача, которая требует некоторых геометрических навыков и терпения. Готовы ли вы? Давайте начнем исследование окружности и попробуем решить эту задачу вместе!

Что значит разделить окружность на равные части?

Разделить окружность на равные части означает разбить ее на несколько сегментов, где каждый сегмент будет иметь одинаковую длину. Это означает, что угол между двумя соседними сегментами будет одинаковым и все сегменты будут иметь одинаковую длину дуги окружности.

Чтобы понять, как разделить окружность на равные части, можно представить ее как круговой график или часы с делениями. Представьте, что вы хотите разделить окружность на восемь равных частей, то есть получить восемь одинаковых сегментов. В этом случае вам потребуется найти угол между каждым сегментом, который будет равен 45 градусам.

Чтобы найти эти углы, можно использовать геометрические методы, алгоритмы или математические формулы. Один из простых способов разделить окружность на равные части — использовать циркуль и линейку. Сначала проведите диаметр окружности, затем проведите лучи, измеряя углы с помощью циркуля и линейки. Таким образом, вы можете разделить окружность на восемь равных сегментов.

Если у вас есть специальное программное обеспечение или графический редактор, вы также можете использовать его для разделения окружности на равные части. В таких программах обычно есть инструменты, которые позволяют вам разделить окружность на равные участки с заданным количеством сегментов.

Разделение окружности на равные части — это не только геометрическая задача, но и интересный способ визуализации данных или создания графических элементов для дизайна. Этот навык может оказаться полезным при создании круговых диаграмм, символов, иконок или других элементов, где необходимо равномерно разделить окружность.

Математический метод для разделения окружности на восемь равных частей

Начнем с того, что окружность состоит из 360 градусов. Мы хотим разделить ее на восемь равных частей, то есть каждая часть должна составлять 45 градусов. Как мы можем это сделать?

Для начала, давайте представим, что мы имеем окружность с центром O и радиусом R. Мы можем провести горизонтальную и вертикальную линии через центр окружности, разделяя ее на четыре равных части.

Затем мы проводим диагонали, соединяющие точки пересечения горизонтальной и вертикальной линий с окружностью. Таким образом, мы получаем основные точки разделения окружности на восемь равных частей. Каждый из этих углов будет составлять 45 градусов.

Теперь, чтобы получить остальные точки разделения окружности на восемь равных частей, нам нужно провести по одной дуге, соединяющей каждую основную точку с соседней основной точкой. Таким образом, мы получим восемь равных секторов, каждый из которых составляет 45 градусов.

Давайте рассмотрим конкретный пример для наглядности. Пусть радиус окружности R равен 5 единицам. Мы проведем горизонтальную и вертикальную линии через центр окружности, получив четыре основные точки разделения окружности. Затем проведем дуги, соединяющие эти точки, чтобы получить остальные точки разделения.

Вы можете представить себе, как все вместе выглядит на плоскости: горизонтальную и вертикальную линии, основные и дополнительные точки разделения. Это всего лишь небольшой пример, но с таким же успехом вы можете разделить окружность на восемь равных частей любой размерности и радиуса.

В завершение, я хотел бы спросить вас: знали ли вы о таком математическом методе для разделения окружности на равные части? И если да, то в каких случаях вам приходилось его использовать? Оставьте свои комментарии ниже!

Применение геометрических принципов: разделение окружности на восемь равных частей

Вы, наверное, задаетесь вопросом, зачем это может понадобиться? Ну, допустим, вы хотите создать красивый логотип, где окружность разделена на восемь секторов одинакового размера. Или, может быть, вам нужно разделить круглый торт с друзьями на восемь равных частей? В любом случае, это задача, которую можно решить с помощью геометрии.

Чтобы разделить окружность на восемь равных частей, мы будем использовать принципы деления окружности на равные углы. Здесь важно помнить, что у окружности всегда 360 градусов. Поэтому равные секторы должны занимать равную часть от этого угла — 45 градусов.

Теперь мы знаем, что нам нужно разделить окружность на 8 равных секторов по 45 градусов каждый. Как же мы это сделаем? Давайте рассмотрим один из способов.

1. На рисунке ниже мы поставим точку O в центре окружности.
2. С помощью циркуля мы проведем две хорды, проходящие через точку O, под углом 45 градусов друг к другу.
3. Теперь проведем перпендикуляры к каждой из этих хорд через точку O. Эти перпендикуляры будут делить окружность на восемь равных секторов.
4. Каждый получившийся сектор будет занимать 45 градусов.

Таким образом, мы разделили окружность на восемь равных частей, используя геометрические принципы. Это простое и элегантное решение задачи.

Надеюсь, эта информация была полезной и вас заинтересовала. Геометрические принципы могут быть очень полезными в повседневной жизни и помогать в решении различных задач. Они позволяют нам видеть мир вокруг нас с новых и интересных сторон.

Использование угловых мер

Итак, как использовать угловые меры для разделения окружности на восемь равных частей? Давайте разберемся.

1. Первым шагом является нахождение центра окружности. Это может быть точка, отмеченная на бумаге или любое другое удобное место.
2. Затем мы рисуем диаметр окружности, которым будем разделять окружность.
3. Следующий шаг — находим середину диаметра и отмечаем ее точкой.
4. После этого мы находим точку на окружности, которая является началом нашего первого сектора окружности. Мы выбираем эту точку по нашему усмотрению.
5. Затем мы измеряем угол между диаметром и линией, проходящей через центр и нашу точку на окружности.
6. Этот угол делится на восемь равных частей с помощью угловых мер. Для этого мы используем градусы — 360 градусов = 2pi радиан = полный угол окружности.
7. Полученная мера угла используется для отметки точек на окружности, которые являются концами каждого сектора. В результате мы получим восемь равных секторов.

Таким образом, используя угловые меры и простые шаги, мы можем разделить окружность на восемь равных частей. Этот метод может пригодиться при создании различных геометрических конструкций, диаграмм или просто для творческих экспериментов.

Практическое руководство: Как разделить окружность на восемь равных частей

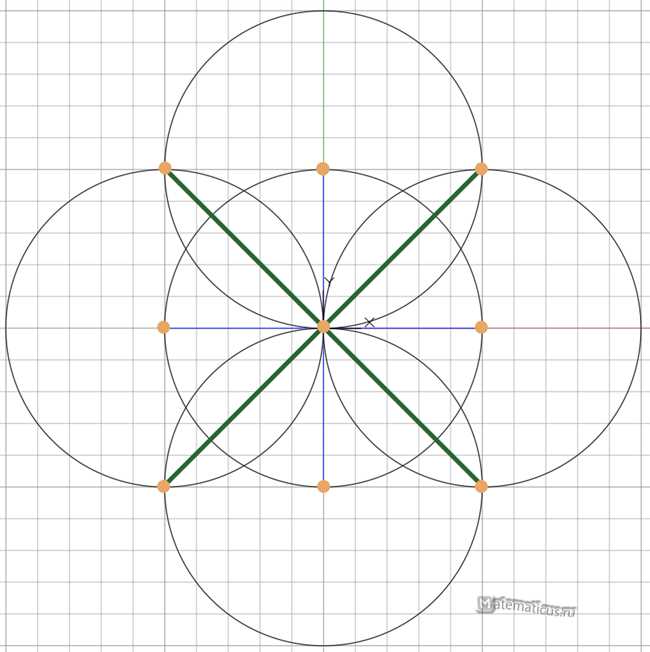
Вот пошаговая инструкция, которая поможет разделить окружность на восемь равных частей:

1. Измерьте радиус окружности с помощью линейки или известной формулы. Обозначим его как «r».
2. Найдите длину окружности с помощью формулы «L=2πr». Здесь «π» представляет собой число Пи, примерное значение которого равно 3,14159.
3. Разделите длину окружности на восемь, чтобы получить длину каждого из восьми сегментов. Формула будет следующей: «l=L/8».
4. Добавьте маркеры на окружности через каждый сегмент длиной «l». Это можно сделать с помощью рулетки и карандаша или других подходящих инструментов.
5. Соедините маркеры линиями, чтобы получить восьмиугольную фигуру, состоящую из восьми равных сегментов окружности. Используйте линейку или другие инструменты для проведения прямых линий.

Поздравляю! Теперь вы разделили окружность на восемь равных частей. Этот практический метод позволяет справиться с задачей даже без специальных программ или сложных вычислений. Не стесняйтесь применять полученные знания и методы в реальных ситуациях, где требуется разделить окружность на равные части.