
Деление дроби на целое число может показаться сложной задачей, но на самом деле это достаточно просто, если знать правила и иметь хорошее понимание дробной арифметики. Для деления дроби на целое число нужно умножить дробь на обратное значение этого числа. Например, чтобы разделить дробь 1/4 на 2, нужно умножить 1/4 на обратное значение 2, то есть 1/2. В результате получим ответ 1/8. Этот принцип действует для любой дроби и любого целого числа. Разбивая примеры и объясняя каждый шаг, мы можем легко понять, как разделить дробь на целое число и получить правильный ответ.
Определение дроби
Для лучшего понимания давайте рассмотрим пример. Представим, что на тарелке у нас есть 3 пирожных, а мы хотим поделить их поровну на 2 части. Возникает вопрос: сколько пирожных будет у каждой части? Ответом на этот вопрос будет дробь 3/2. Числитель 3 означает, что у каждой части будет по 3 пирожных, а знаменатель 2 говорит о том, что мы делим на 2 части. Таким образом, дробь 3/2 представляет собой результат деления 3 пирожных на 2 части.
В обычной жизни мы часто сталкиваемся с дробями, например, при измерении времени, расстояния или доли какого-то объекта. Поэтому важно понимать, как работать с дробями и как выполнять различные операции с ними, включая деление.
Техника деления дроби на целое число
Перед тем, как приступить к делению дроби на целое число, важно понять, что деление в математике является обратной операцией умножения. Если мы умножаем одно число на другое, то результатом будет третье число. Обратный процесс деления позволяет нам найти один из множителей, зная два других числа.
Итак, давайте рассмотрим пример деления дроби на целое число. Предположим, у нас есть дробь 3/4, и мы хотим разделить ее на целое число 2. Как нам это сделать?
Шаг 1: Используйте знак деления
Первым шагом при делении дроби на целое число является размещение знака деления (/) между дробью и целым числом.
В нашем примере это будет выглядеть так: 3/4 ÷ 2.
Шаг 2: Выполните деление числителя
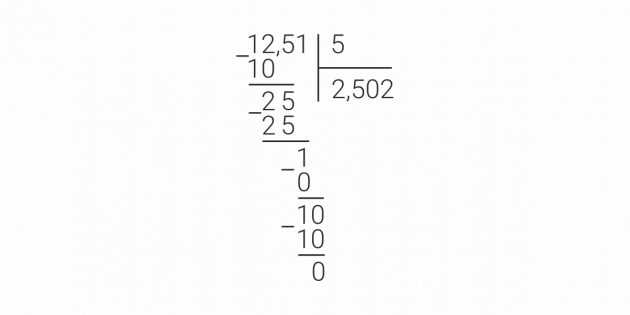
Вторым шагом является выполнение обычного деления числителя дроби на целое число.
В нашем примере мы делим числитель 3 на целое число 2: 3 ÷ 2 = 1.5.
Шаг 3: Не забудьте делить знаменатель
Третий и последний шаг — деление знаменателя дроби на целое число.
В нашем примере мы делим знаменатель 4 на целое число 2: 4 ÷ 2 = 2.
Итоговый результат
Теперь мы можем записать результаты нашего деления — числитель и знаменатель — в виде новой дроби.
В нашем примере результатом будет дробь 1.5/2.
Вот и все! Теперь мы знаем, как делить дробь на целое число. Не забывайте, что деление дроби на целое число может давать как десятичные, так и обыкновенные дроби. Всегда проверяйте результаты и убедитесь, что они точны.
Примеры деления дробей на целые числа
При делении дроби на целое число необходимо следовать определенным правилам. В результате получается новая дробь, значение которой меньше исходной дроби. Вот несколько примеров, которые помогут вам лучше понять этот процесс.
Пример 1:
Деление дроби 2/3 на целое число 2:
- Сначала умножим знаменатель дроби на целое число: 3 * 2 = 6.
- Затем умножим числитель дроби на то же целое число: 2 * 2 = 4.
- Таким образом, получаем новую дробь 4/6.
Пример 2:

Деление дроби 5/8 на целое число 4:
- Умножаем знаменатель дроби на 4: 8 * 4 = 32.
- Умножаем числитель дроби на 4: 5 * 4 = 20.
- Получаем новую дробь 20/32.
Пример 3:
Деление дроби 3/4 на целое число 5:
- Умножаем знаменатель дроби на 5: 4 * 5 = 20.
- Умножаем числитель дроби на 5: 3 * 5 = 15.
- Итак, новая дробь равна 15/20.
Во всех этих примерах мы видим, что результатом деления дроби на целое число является новая дробь, которая имеет меньшее значение, чем исходная. При необходимости такую дробь можно упростить или привести к микроформе.






