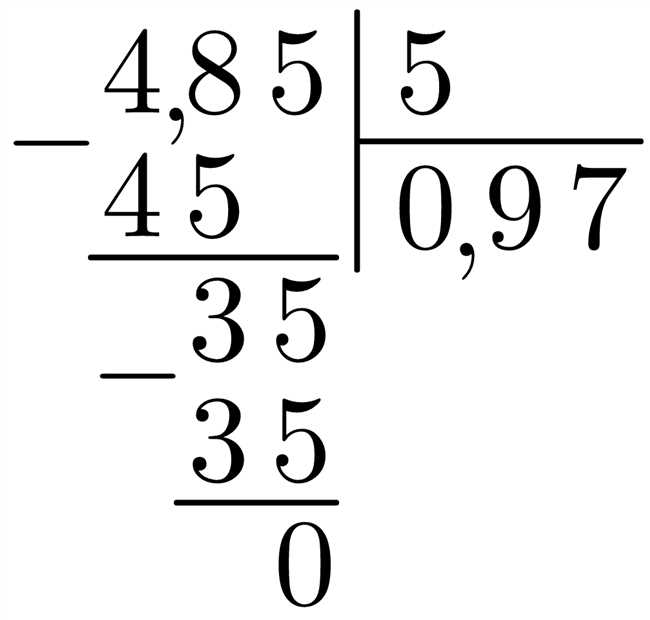
Когда мы имеем дело с целым числом и дробью, возникает вопрос о том, как их разделить. Взглянув на это, казалось бы, сложное математическое действие, вы увидите, что существуют простые способы сделать это.
Первый способ — деление числителя на знаменатель вручную. Вы просто делите целое число на числитель и записываете результат в виде десятичной дроби.
Второй способ — использование десятичных дробей. Если у вас есть десятичное представление дроби, вы можете просто разделить целое число на это десятичное представление.
В обоих случаях вы получите результат разделения целого числа на дробь.
Основные понятия и определения
Здесь рассматриваются основные понятия и определения, связанные с разделением целых чисел на дробные числа. Понимание этих терминов поможет вам более глубоко разобраться в процессе деления и использовать различные методы эффективно.
Целое число — это число, которое не имеет дробной части и может быть положительным или отрицательным. Например, 5, -3 и 0 являются целыми числами.
Дробь — это число, представленное отношением двух чисел: числителя и знаменателя. Числитель указывает, сколько частей целого представляет собой дробь, а знаменатель указывает, на сколько частей целое число было разделено. Например, 3/4 — это дробь, представляющая собой три четверти целого числа.
Деление — это операция, которая позволяет разделить одно число на другое, чтобы получить результат. В контексте разделения целых чисел на дробные числа, мы хотим узнать, сколько раз дробное число умещается в целое число.
Частное — результат деления двух чисел. В случае разделения целого числа на дробное число, частное будет также дробным числом, указывающим, сколько раз дробь умещается в целое число.
Остаток — это остаток от деления, который остается после того, как дробное число умещается в целое число столько раз, насколько это возможно. Остаток может быть представлен в виде дроби или десятичной дроби в зависимости от требований задачи.
Используя эти понятия и определения, вы можете эффективно разделять целые числа на дробные числа и решать задачи, связанные с этим процессом. Знание этих основных терминов поможет вам разбираться в математике легче и быстрее, делая образование более доступным и интересным.
Целое число и дробь
С другой стороны, дроби представляют собой числа, которые состоят из двух частей: числителя и знаменателя. Числитель указывает, сколько частей целого числа мы имеем, и обычно представляется в виде десятичной дроби или десятичной дроби. Знаменатель указывает, на сколько частей целого числа мы разделили числитель и обычно представляется в виде целого числа. Дроби могут быть представлены в виде ½, 1/3, 4/5 и так далее.
Разделение целого числа на дробь может быть выполнено, используя различные методы, такие как:
- Перевод дроби в десятичную форму и выполнение деления целого числа на десятичную дробь с помощью обычного деления.
- Использование метода умножения обеих частей дроби на знаменатель для превращения дроби в целое число, а затем выполнение деления целого числа на полученное целое число.
Для успешного деления целого числа на дробь важно использовать соответствующие математические операции и при этом быть внимательным к правилам математики. При правильном использовании методов и тщательном рассмотрении целого числа и дроби, вы сможете успешно разделить целое число на дробь и получить точный результат.
Простой способ деления целого числа на дробь
Давайте представим ситуацию: у вас есть целое число, например, 10, и вы хотите разделить его на дробь, например, 1/4. Как это сделать просто и без лишних сложностей? Давайте разберемся.
Первым шагом в делении целого числа на дробь является изменение дроби на эквивалентную ей дробь с целым числом в знаменателе. В нашем примере, 1/4 можно изменить на 4/1, что делает деление намного проще.
Теперь мы можем использовать простую формулу для деления двух целых чисел. Для этого мы домножаем числитель и знаменатель целой части дроби на одно и то же число, чтобы получить целое число и сохранить пропорцию. В нашем примере это будет 10 * 4 = 40.
Итак, результат деления 10 на 1/4 составляет 40. Просто, не правда ли?
Однако, если у вас возникают трудности с пониманием этого метода, я могу поделиться с вами примером из реальной жизни. Представьте, что у вас есть пирог, и вам нужно разделить его на 4 равные части. Если вы разрежете пирог на четыре части, каждая часть будет составлять 1/4 пирога. Если вы хотите узнать, сколько пирога приходится на одну часть, вам просто нужно умножить размер пирога на количество частей: 10 * 4 = 40.
Таким образом, простой способ деления целого числа на дробь заключается в изменении дроби на эквивалентную ей дробь с целым числом в знаменателе и применении формулы для деления двух целых чисел. И помните, практика делает мастера!
Алгоритм десятичного деления
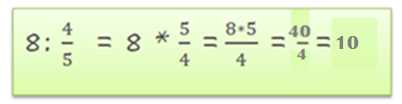
Разделение целого числа на дробь может показаться сложным процессом, но на самом деле существует простой алгоритм, который позволяет выполнить это действие. Этот алгоритм называется алгоритмом десятичного деления и легко применим в повседневных ситуациях.
Первым шагом алгоритма является разделение целого числа на дробь. Например, предположим, что мы хотим разделить число 15 на 2/3. Сначала мы записываем делитель (дробь) на левой стороне и делимое (целое число) на правой стороне:
| 2/3 | 15 |
Затем мы начинаем делить, смотря на цифры в делимом числе слева направо. Делим первую цифру 1 на делитель 2 (1 ÷ 2 = 0,5) и записываем результат под делимым числом:
| 2/3 | 15 |
| 0,5 |
Теперь мы перемещаемся к следующей цифре в делимом числе и делим 15 на 2. Результатом будет 7 с остатком 1 (15 ÷ 2 = 7, остаток 1). Записываем результат под предыдущим результатом:
| 2/3 | 15 |
| 0,57 |
Затем перемещаемся к следующей цифре в делимом числе, которой больше нет, и добавляем ноль справа от результата:
| 2/3 | 15 |
| 0,5710 |
Далее мы продолжаем деление, добавляя ноль в конце результата и делим 10 на 2. Результатом будет 5 без остатка (10 ÷ 2 = 5). Записываем результат под предыдущим результатом, добавляя еще одну ноль в конце:
| 2/3 | 15 |
| 0,57105 |
Продолжаем деление, добавляя ноль в конце результата и делим 5 на 2. Результатом будет 2 без остатка (5 ÷ 2 = 2). Записываем результат под предыдущим результатом, добавляя еще одну ноль в конце:
| 2/3 | 15 |
| 0,571052 |
Продолжаем деление, добавляя ноль в конце результата и делим 2 на 2. Результатом будет 1 без остатка (2 ÷ 2 = 1). Записываем результат под предыдущим результатом, добавляя еще одну ноль в конце:
| 2/3 | 15 |
| 0,5710521 |
В конце деления мы получаем результат 0,5710521. Это означает, что целое число 15 делится на дробь 2/3 и результат равен 0,5710521.
Алгоритм десятичного деления может быть использован для разделения целых чисел на любые дроби. Это важный навык, который может быть полезным в повседневной жизни, при решении задач по математике или финансовым расчетах. Попрактикуйтесь в его применении и вы станете более уверенными в разделении целых чисел на дроби!
Шаг 1: Приведение дроби к десятичному виду
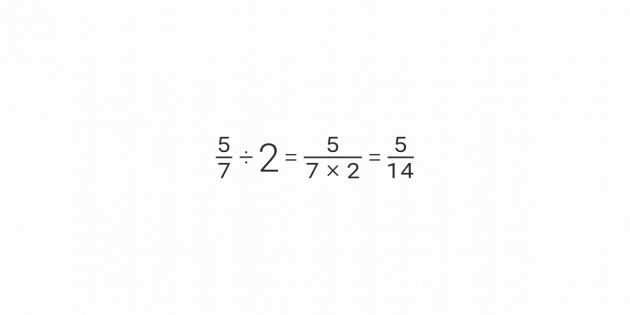
Когда вам нужно разделить целое число на дробь, первым шагом будет приведение дроби к десятичному виду. Это необходимо для того, чтобы получить точное значение результата деления.
Прежде всего, вспомним, что десятичная дробь состоит из двух частей: десятичной целой части, которая перед точкой, и десятичной дробной части, которая следует после точки.
Начнем с примера. Допустим, у нас есть дробь 2/3, которую мы хотим разделить на целое число, скажем, 5.
Шаг 1: Переведите дробь в вид десятичной дроби. Для этого разделите числитель на знаменатель.
В нашем примере 2/3, числитель равен 2 и знаменатель равен 3. Поделим 2 на 3: 2 ÷ 3 = 0.6666666666667 (бесконечная десятичная дробь).
Теперь у нас есть десятичная дробь 0.6666666666667.
При переводе дроби в десятичное число, мы всегда должны помнить, что десятичное число может быть представлено ограниченным или бесконечным числом знаков после запятой.
В нашем случае дробь 2/3 представлена бесконечной десятичной дробью 0.6666666666667, причем «6» повторяется в конце. Возможно, вы задаете вопрос: какое количество знаков после запятой нам нужно использовать?
Количество знаков после запятой зависит от точности, которую вы хотите достичь. В некоторых случаях ограниченная десятичная запись может быть достаточной, например, если вам нужно только одно или два знака после запятой.
Однако в большинстве случаев мы стараемся использовать максимальное количество знаков после запятой, чтобы получить наиболее точный результат.
Таким образом, в первом шаге мы приводим дробь к десятичному виду, то есть представляем ее в виде ограниченной или бесконечной десятичной дроби.
Шаг 2: Расстановка нулей после запятой
Теперь, когда мы разделили целое число на дробь, давайте поговорим о расстановке нулей после запятой. Нули после запятой играют важную роль в точном представлении результата деления.
Для расстановки нулей после запятой, нам нужно понять, какое количество нулей нужно использовать в ответе. Для этого мы можем рассмотреть количество чисел после запятой в дроби и количество возможных десятичных разрядов целого числа.
Начнем с простого примера. Предположим, у нас есть целое число 5 и дробь 1/2. После деления 5 на 1/2, получим результат 10. В этом случае нам не нужно добавлять нули после запятой, так как результат уже является целым числом.
Однако, когда у нас есть дробь с периодическими числами, нам нужно задуматься о том, сколько нулей следует добавить после запятой. Например, если у нас есть целое число 4 и дробь 1/3, после деления получим результат 1.3333… В этом случае мы можем добавить один ноль после запятой, чтобы получить более точное представление результата: 1.0.
Теперь рассмотрим пример с десятичными разрядами целого числа. Предположим, у нас есть целое число 7 и дробь 1/4. После деления получим результат 28. В этом случае у нас нет чисел после запятой в дроби, поэтому нет необходимости добавлять нули после запятой.
Таким образом, для расстановки нулей после запятой, мы должны учесть количество чисел после запятой в дроби и количество возможных десятичных разрядов целого числа. Мы можем добавлять нули после запятой в соответствии с этими параметрами, чтобы получить более точное представление результата деления.
Шаг 3: Выполнение десятичного деления
В данной статье мы рассмотрели простые способы разделения целого числа на дробь. На предыдущих шагах мы научились выделять дробную часть числа и определить периодическую десятичную дробь, а теперь самое время выполнить деление.
Для выполнения десятичного деления нам необходимо следовать нескольким шагам:
- Разделим целую часть числа на дробь, удалив запятую. Это позволит нам получить первую цифру результата деления.
- Проведем операцию вычитания, умножив полученную цифру на дробь и вычтя результат из целой части исходного числа.
- Умножим результат вычитания на 10 и полученное число разделим на дробь. Это даст нам следующую цифру результата деления.
- Повторим шаги 2 и 3 до тех пор, пока не получим необходимую точность или не найдем периодическую десятичную дробь.
Выполнение десятичного деления является важным этапом при работе с дробными числами и позволяет получить точный результат. Используя описанные выше шаги, вы с легкостью сможете разделить целое число на дробь и получить результат с нужной точностью. Удачи вам!






