
Когда речь идет о дробях, некоторые из них могут быть неправильными, что означает, что числитель больше знаменателя. Приведение неправильной дроби к правильной может показаться сложной задачей, но на самом деле это довольно просто, если вы знаете правильные советы и приемы. В этой статье мы рассмотрим несколько полезных подходов, которые помогут вам привести неправильную дробь к правильной. Будем разбирать конкретные примеры и рассмотрим шаги, которые необходимо предпринять для выполнения данной операции. Если вы хотите научиться правильно приводить дроби, то эта статья для вас. Продолжайте читать!
Способ 1: Превращение неправильной дроби в смешанную
Для превращения неправильной дроби в смешанную, вам необходимо выполнить следующие шаги:
- Деление числителя на знаменатель.
- Если результат деления дает целое число без остатка, то это число будет являться целой частью смешанной дроби.
- Если результат деления дает дробное число, то первая цифра после запятой будет целой частью смешанной дроби.
- Остаток после деления становится числителем правильной дроби, а знаменатель остается прежним.
Давайте рассмотрим пример:
Дана неправильная дробь 7/3. Чтобы превратить ее в смешанную, мы делим 7 на 3. Результат деления равен 2 и есть остаток 1. Так что мы можем записать исходную неправильную дробь 7/3 как смешанную дробь 2 1/3.
Преобразование неправильной дроби в смешанную делает математические вычисления и понимание дробей проще. Кроме того, смешанные дроби могут быть более наглядными, особенно когда речь идет о представлении долей или количеств в повседневной жизни.
Теперь, когда вы знаете, как превратить неправильную дробь в смешанную, вы можете использовать этот способ, чтобы лучше понимать и работать с дробями. Попробуйте применить этот метод на практике и задайте себе вопрос: какая будет смешанная дробь для неправильной дроби 5/2?
Способ 2: Приведение неправильной дроби к правильной путем деления
Если у вас есть неправильная дробь, то вы можете привести ее к правильной с помощью деления. Этот способ довольно прост, но требует некоторых математических навыков.
Чтобы привести неправильную дробь к правильной, вам нужно разделить числитель на знаменатель. Затем полученный результат станет целой частью правильной дроби, а остаток станет новым числителем в дробной части.
Давайте посмотрим на пример, чтобы лучше понять этот способ. Рассмотрим неправильную дробь 7/3.
Шаг 1: Делим числитель (7) на знаменатель (3):
7 ÷ 3 = 2 целые части и остаток 1
Шаг 2: Целая часть (2) становится целой частью правильной дроби, а остаток (1) становится новым числителем в дробной части:
2 1/3
Таким образом, неправильная дробь 7/3 приводится к правильной дроби 2 1/3.
Теперь попробуем решить другой пример. Представим, что у нас есть неправильная дробь 11/5.
Шаг 1: Делим числитель (11) на знаменатель (5):
11 ÷ 5 = 2 целые части и остаток 1
Шаг 2: Целая часть (2) становится целой частью правильной дроби, а остаток (1) становится новым числителем в дробной части:
2 1/5
Таким образом, неправильная дробь 11/5 приводится к правильной дроби 2 1/5.
Получается, что приведение неправильной дроби к правильной путем деления очень простой процесс. Он позволяет лучше понять дроби и делать с ними различные математические операции.
Вместе с тем, этот метод приведения дает возможность представить дроби в более понятной и удобной форме.
Заключение:
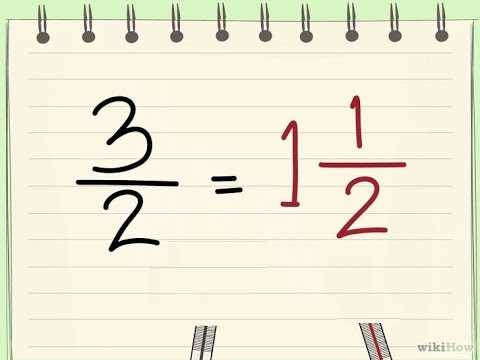
Сокращение неправильной дроби позволяет получить эквивалентную дробь с меньшими числителем и знаменателем, что делает ее более удобной для работы. Этот метод особенно полезен при выполнении различных операций с дробями, таких как сложение, вычитание, умножение и деление.
Чтобы упростить неправильную дробь, нужно найти наибольший общий делитель числителя и знаменателя и разделить каждое из них на этот делитель. Итоговая дробь будет эквивалентной исходной, но более простой и легче воспринимаемой.
- Выполняйте сокращение дроби, если числитель и знаменатель имеют общие множители;
- Проверяйте результат, чтобы убедиться, что полученная дробь правильная;
- Используйте этот способ для упрощения неправильных дробей в различных задачах.
Способ 3: Упрощение неправильной дроби путем сокращения – это простой и эффективный способ привести дробь к правильной форме. С его помощью вы сможете упростить вычисления и более легко работать с дробями в математических задачах.






