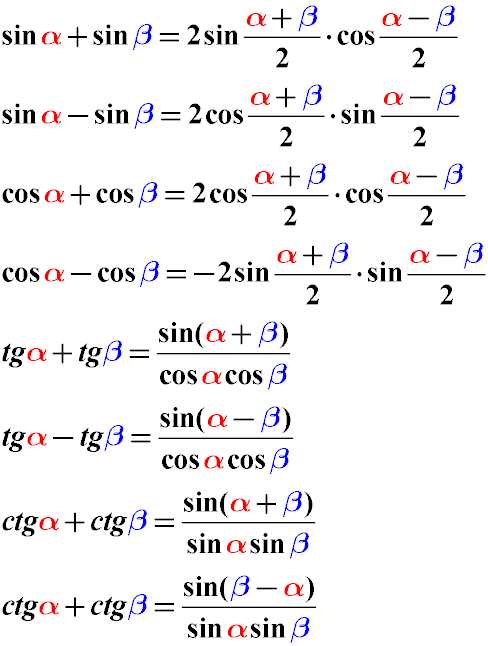
Преобразование тангенса в синус — это удобный и полезный прием, который часто используется в математике и физике. Этот простой процесс позволяет нам выразить тангенс как функцию синуса и упростить вычисления. Для преобразования тангенса в синус мы используем фундаментальное соотношение между этими тригонометрическими функциями. Зная эту связь, мы можем преобразовать уравнение или выражение, содержащее тангенс, в эквивалентное выражение, содержащее только синус. Это практическое руководство покажет вам, как выполнить это преобразование шаг за шагом, чтобы упростить вашу работу и достичь более точных результатов. Чтобы начать, давайте рассмотрим основное соотношение между тангенсом и синусом и разберем примеры его использования в практических задачах.
Понимание базовых тригонометрических функций
Синус
Синус угла в простейшем случае можно представить как отношение противоположной стороны к гипотенузе в прямоугольном треугольнике. Он обозначается как sin(θ), где θ — это угол.
Значение синуса всегда лежит в диапазоне от -1 до 1.
Косинус
Косинус угла в простейшем случае можно представить как отношение прилежащей стороны к гипотенузе в прямоугольном треугольнике. Он обозначается как cos(θ).
Значение косинуса также всегда лежит в диапазоне от -1 до 1.
Тангенс
Тангенс угла в простейшем случае можно представить как отношение противоположной стороны к прилежащей стороне в прямоугольном треугольнике. Он обозначается как tan(θ).
Значение тангенса может быть любым числом, так что он не имеет ограничений, как синус и косинус.
Важно понимать, что значения синуса, косинуса и тангенса зависят от величины угла. Тригонометрические функции широко применяются в различных областях знаний, включая математику, физику, инженерию, астрономию и другие науки.
Что такое тангенс?
Окей, рассмотрим это на примере. Представь, что ты стоишь в начале координатной плоскости, и у тебя есть треугольник с некоторым углом. Тангенс этого угла — это отношение длины противолежащего катета (той стороны треугольника, которая не прилегает к оси абсцисс) к длине прилегающего катета (стороны треугольника, которая прилегает к оси абсцисс).
То есть, если угол равен α, противолежащий катет равен a, а прилегающий катет равен b, то тангенс угла α будет равен a/b.
Но зачем нам знать значение тангенса угла? Отличный вопрос! Тангенс является основой для вычисления других тригонометрических функций, таких как синус и косинус.
Что такое синус?
Для лучшего понимания синуса, давайте представим прямоугольный треугольник. В прямоугольном треугольнике один из углов равен 90 градусов (прямой угол), а остальные два угла называются острыми углами. Синус острого угла определяется как отношение противоположной стороны к гипотенузе треугольника.
Аналогично, мы можем использовать синус для вычисления острых углов на основе известных значений длины сторон треугольника. Он позволяет нам решать различные геометрические и физические задачи, такие как определение высоты объекта или расчет угла наклона плоскости.
В математике синус часто обозначается символом «sin». Он может принимать значения от -1 до 1, что означает, что синус острого угла всегда меньше или равен длине гипотенузы треугольника.
Использование синуса может быть весьма полезным и увлекательным. Например, вы можете использовать синус для решения головоломок и задач по геометрии, а также для создания красивых и сложных графических изображений. Он также является основой для других тригонометрических функций, таких как косинус и тангенс, которые вместе предоставляют полный набор угловых отношений.
Как преобразовать тангенс в синус
Перед тем, как приступить к преобразованию, давайте вспомним, что такое тангенс и синус. Тангенс угла в треугольнике определяется как отношение противоположного катета к прилежащему катету, тогда как синус — это отношение противоположного катета к гипотенузе. Оба эти понятия тесно связаны, и их можно преобразовывать друг в друга.
Итак, как преобразовать тангенс в синус? Для этого нам понадобится выразить синус через катеты и гипотенузу в соответствующем треугольнике. Если у нас уже есть значение тангенса угла, мы можем использовать его для нахождения синуса.
Давайте рассмотрим пример. Предположим, у нас есть значение тангенса угла: тангенс a = 0.8. Нам нужно выразить синус через этот тангенс и найти его значение.
Один из способов осуществить это преобразование — использовать тригонометрическую формулу связи тангенса и синуса:
Синус a = тангенс a / √(1 + (тангенс a)²)
В нашем случае, подставив значение тангенса a = 0.8 в эту формулу, мы получим:
Синус a = 0.8 / √(1 + 0.8²)
После простых математических операций, включающих возведение в квадрат и извлечение квадратного корня, можно получить значение синуса. В нашем случае, значение синуса будет равно приблизительно 0.6.
Таким образом, мы успешно преобразовали значение тангенса в соответствующее значение синуса. Это преобразование может быть полезным, когда нам необходимо работать с функциями синуса, основанными на значениях тангенса углов.
Обратите внимание, что синус и тангенс — это функции, которые зависят от угла. Поэтому, если вы хотите преобразовать значение тангенса в синус для конкретного угла, убедитесь, что используете правильную формулу и подставляете правильное значение угла.
Использование основной тригонометрической формулы
Когда мы говорим о преобразовании тангенса в синус, важно понимать основную тригонометрическую формулу. Эта формула гласит:
синус угла равен отношению противолежащего катета к гипотенузе.
Выражение «противолежащий катет» относится к стороне треугольника, которая лежит напротив угла, а «гипотенуза» — это наибольшая сторона, которая является основой треугольника. Основная тригонометрическая формула объясняет взаимосвязь между синусом и тангенсом.
Прежде чем мы сможем использовать основную тригонометрическую формулу для преобразования тангенса в синус, нам нужно узнать значения угла и сторон треугольника. Чтобы сделать это, мы можем использовать другие тригонометрические формулы или таблицы синусов, косинусов и тангенсов. Но не спешите! Как можно использовать основную тригонометрическую формулу, если у нас уже есть тангенс?
Немного творческого мышления и применение простых математических операций могут нам помочь. Вспомни, что тангенс определяется как отношение противолежащего катета к прилегающему катету. Если мы знаем угол, величина тангенса и значение противолежащего катета, мы можем легко найти прилежащий катет и гипотенузу, а затем использовать основную тригонометрическую формулу для преобразования тангенса в синус.
Например, представьте, что у нас есть треугольник со сторонами, а угол A, противолежащий катет a и тангенс с. Мы знаем, что тангенс равен отношению противолежащего катета к прилежащему катету, что можно записать следующим образом:
тангенс A = a/c.
Теперь мы можем решить уравнение относительно прилегающего катета:
a = c * тангенс A.
Когда мы получаем значения противолежащего катета и гипотенузы, мы можем использовать основную тригонометрическую формулу, чтобы найти значение синуса.
Вот и все! Теперь вы знаете, как использовать основную тригонометрическую формулу для преобразования тангенса в синус. Важно понимать базовые принципы тригонометрии и быть в состоянии адаптировать и применять их в различных ситуациях. Удачи!
Заключение
В данной статье мы изучили преобразование тангенса в синус и рассмотрели несколько примеров его применения. Теперь вы знаете, как преобразовать тангенс в синус и использовать этот прием в решении математических задач.
Преобразование тангенса в синус может быть полезно при решении уравнений и задач, связанных с геометрией и тригонометрией. Оно позволяет упростить выражения, сократить количество элементов и упростить вычисления. Также преобразование тангенса в синус можно использовать для получения эквивалентных выражений и доказательства различных тригонометрических тождеств.
Для преобразования тангенса в синус достаточно знать соответствующее тригонометрическое тождество и применить его. Возможность преобразования тангенса в синус упрощает решение многих задач и повышает качество математических вычислений.
Примеры преобразования тангенса в синус:
- Пример 1: решение уравнения, содержащего тангенс, путем преобразования его в синус.
- Пример 2: упрощение и упрощение выражений с помощью преобразования тангенса в синус.
- Пример 3: доказательство тригонометрического тождества путем преобразования тангенса в синус.
Использование преобразования тангенса в синус может значительно упростить решение математических задач и облегчить работу с тригонометрическими выражениями. Это мощный инструмент, который стоит изучить и применять в своей практике.






