Как преобразовать неправильную дробь в правильную: подробное руководство
Если у вас есть неправильная дробь, то вы, возможно, заинтересованы в ее преобразовании в правильную. Превращение неправильной дроби в правильную поможет вам лучше понять ее значение и использование в математических расчетах.
Процесс преобразования неправильной дроби в правильную включает в себя деление числителя на знаменатель и запись остатка в виде смешанной дроби. Это позволяет наглядно представить доли и сделать их более понятными.
В этом руководстве мы предоставим вам пошаговую инструкцию о том, как преобразовать неправильную дробь в правильную, а также объясним основные концепции, связанные с этим процессом. Следуя этим шагам, вы сможете легко преобразовать неправильную дробь и использовать ее в своих математических расчетах.
Определение неправильной дроби
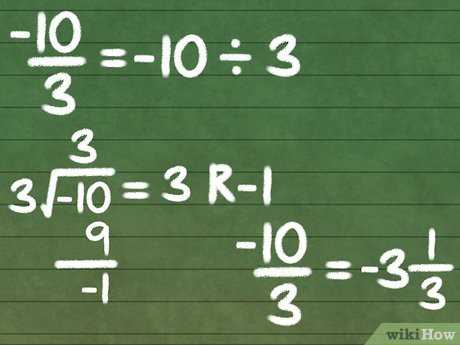
Неправильная дробь имеет числитель, который превышает знаменатель и не может быть представлен в виде целого числа и остатка. Например, дробь 7/4 является неправильной, потому что числитель 7 больше знаменателя 4.
Неправильные дроби могут быть выражены в виде смешанных чисел, которые состоят из целой части и правильной дроби. Например, неправильная дробь 7/4 может быть представлена в виде смешанного числа 1 3/4, где целая часть равна 1, а правильная дробь равна 3/4.
Неправильные дроби могут быть использованы для представления дробных частей числа или результатов деления. Они могут быть преобразованы в правильные дроби или смешанные числа для более удобного представления и сравнения.
Преобразование неправильной дроби в правильную дробь может быть полезной операцией при решении математических задач или вычислениях. Она позволяет представить дробь в более простой и удобной форме.
Понятие правильной дроби

Важно понимать, что правильная дробь не обязательно должна быть положительной. Она может быть и отрицательной, например, -1/4 или -3/5. Знак минус указывает на то, что дробь меньше нуля.
Правильные дроби имеют множество практических применений и широко используются в нашей повседневной жизни. Они могут представлять доли, проценты, вероятности, отношения и многое другое. Например, когда мы говорим о том, что мы съели половину пирога или потратили 75% своего времени на выполнение задания, мы используем правильные дроби.
Наиболее распространенные методы для преобразования неправильной дроби в правильную включают деление числителя на знаменатель или упрощение дроби до наименьшего объемного выражения. Если, например, у нас есть дробь 17/5, мы можем разделить 17 на 5, что даст нам 3 и остаток дроби 2/5. Теперь у нас есть правильная дробь 3 2/5.
Упрощение дроби до наименьшего объемного выражения является другим способом преобразования неправильной дроби в правильную. Для этого нужно найти наибольший общий делитель числителя и знаменателя и разделить оба числа на этот делитель. Например, если у нас есть дробь 28/4, то наибольший общий делитель чисел 28 и 4 равен 4. Если мы разделим и числитель, и знаменатель на 4, мы получим правильную дробь 7/1.
Важно разобраться с преобразованием неправильной дроби в правильную, чтобы лучше понимать и использовать дроби в различных математических задачах и повседневных ситуациях. Попробуйте применить эти методы и поиграйтесь с неправильными дробями, чтобы стать более опытным в их обработке. Задавайте себе вопросы о значении этих дробей в реальной жизни и ищите их применение вокруг себя. Математика всегда будет одной из важных сторон нашей жизни, и правильные дроби — это один из ее ключевых компонентов.
Почему требуется преобразование неправильной дроби в правильную?
Преобразование неправильной дроби в правильную необходимо для удобства и упрощения математических вычислений, а также для лучшего понимания и интерпретации числовых значений.
Когда числитель превышает знаменатель неправильной дроби, мы сталкиваемся с неудобством в работе с числами. Приведение неправильной дроби к правильной форме позволяет нам иметь более ясное представление о ее значении и легко производить операции с ней.
Неправильная дробь может быть выражена с использованием целого числа и обыкновенной дроби. Это позволяет нам точнее определить значение дроби и легче сравнивать ее с другими числами. Например, если у нас есть неправильная дробь 7/3, то мы можем преобразовать ее в правильную дробь 2 1/3. Это позволяет нам лучше понять, что дробь имеет значение больше, чем 2, но меньше, чем 3, и легче использовать ее в дальнейших вычислениях.
Кроме того, преобразование неправильной дроби в правильную упрощает сравнение и сортировку дробей. Это особенно полезно при работе с большим количеством дробей, где правильная форма позволяет нам легко сравнивать их и проводить различные математические операции.
Также, правильная дробь является более простой и интуитивно понятной формой для большинства людей, в том числе для детей. Преобразование неправильной дроби в правильную позволяет упростить математические концепции и сделать их более доступными для понимания и использования.
Шаги для преобразования неправильной дроби в правильную
Преобразование неправильной дроби в правильную может показаться сложной задачей, но на самом деле это довольно просто, если вы знаете правильные шаги. В этом подробном руководстве я расскажу о том, как преобразовать неправильную дробь в правильную с максимальным комфортом. Давайте начнем!
- Определите целую часть: Неправильная дробь представляет собой дробь с числителем, который больше знаменателя. Первым шагом является определение целой части этой дроби. Целая часть это просто число, которое прибавляется к правильной дроби.
- Вычитайте целую часть и запишите остаток: После того, как вы определили целую часть, обычно остается остаток. Это остаток представляет собой дробь с тем же знаменателем, но с числителем, который меньше знаменателя. Остаток будет числителем правильной дроби.
- Упростите правильную дробь: Если возможно, упростите дробь. Для этого найдите общий делитель числителя и знаменателя и разделите оба числа на него. Это поможет вам записать дробь в наиболее простой форме.
- Запишите правильную дробь: Теперь, когда у вас есть правильная дробь, вам нужно ее записать. Возьмите остаток (числитель дроби) после того, как вычли целую часть, и запишите его как числитель. Знаменатель будет таким же, как у исходной неправильной дроби.
И вот вы уже закончили! Вы успешно преобразовали неправильную дробь в правильную, используя всего несколько простых шагов. Эти шаги могут быть повторены с любой неправильной дробью, позволяя вам легко превратить их в правильные дроби.
Так что не бойтесь неправильных дробей! Следуйте этим шагам и переведите их в правильные дроби с легкостью. Практикуйтесь с различными примерами, чтобы стать в этом еще более искусным, и вскоре это станет для вас рутиной. Удачи вам!
Практические примеры и упражнения
В ходе этой статьи мы рассмотрели различные методы и шаги, необходимые для преобразования неправильной дроби в правильную. Но чтобы лучше усвоить эту информацию, давайте проведем несколько практических примеров и упражнений.
1. Преобразование неправильной дроби в правильную:
- Пример: 7/4
- Шаги:
- Делим числитель на знаменатель: 7 ÷ 4 = 1
- Оставляем остаток: 7 — 1 × 4 = 3
- Ответ: 1 3/4
2. Преобразование неправильной дроби в смешанную:
- Пример: 13/5
- Шаги:
- Делим числитель на знаменатель: 13 ÷ 5 = 2
- Оставляем остаток: 13 — 2 × 5 = 3
- Ответ: 2 3/5
3. Преобразование смешанной дроби в неправильную:
- Пример: 2 3/4
- Шаги:
- Умножаем целую часть на знаменатель: 2 × 4 = 8
- Складываем полученное значение с числителем: 8 + 3 = 11
- Ответ: 11/4
Попробуйте выполнить эти упражнения самостоятельно, чтобы получить практическую навык и лучше понять процесс преобразования неправильной дроби в правильную или смешанную. Постепенно это станет привычкой, и вы сможете легко работать с дробями в повседневной жизни или в математических задачах.
Теперь, когда вы овладели этими базовыми методами, вы можете применять их в любой ситуации, где требуется преобразование дроби. Уверены, что с вашими новыми знаниями вы сможете справиться с любыми задачами, связанными с дробями!






