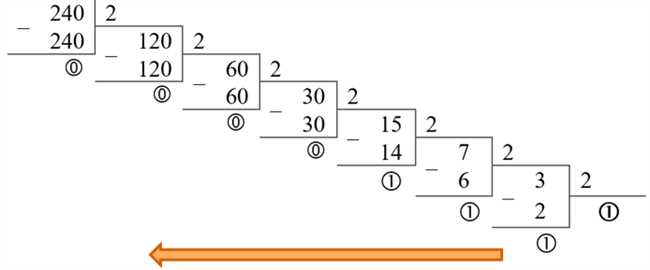
Как представляется число 5 в двоичной системе счисления? Это вопрос, который может вызвать некоторую путаницу. В двоичной системе счисления используются только две цифры — 0 и 1. Число 5 можно представить в двоичной системе как «101». Здесь первая цифра представляет 4 (2 в степени 2), вторая цифра — 0 (2 в степени 1) и третья цифра — 1 (2 в степени 0). Поэтому число 5 в двоичной системе записывается как «101». Это может показаться необычным для тех, кто привык к десятичной системе счисления, где используются все десять цифр. Однако, для компьютеров и электронных устройств, которые часто используют двоичную систему счисления, это является обычной практикой.
Что такое двоичная система счисления?
Основная идея двоичной системы счисления заключается в том, что каждая позиция числа имеет свою собственную степень двойки. Например, в двоичном числе 1010 первая позиция слева (самая правая цифра) имеет вес 2^0 (равен 1), вторая позиция имеет вес 2^1 (равен 2), третья позиция имеет вес 2^2 (равен 4), а четвертая позиция имеет вес 2^3 (равен 8).
Когда мы записываем число в двоичной системе счисления, мы умножаем каждую цифру на ее вес в степени двойки и складываем полученные произведения. Например, для числа 1010 мы получим:
- 1 * 2^3 = 8
- 0 * 2^2 = 0
- 1 * 2^1 = 2
- 0 * 2^0 = 0
При сложении всех произведений мы получим общую сумму 8 + 0 + 2 + 0 = 10. Таким образом, число 1010 в двоичной системе счисления представляет собой десятичное число 10.
Двоичная система счисления имеет множество применений в нашей повседневной жизни, особенно в области информационных технологий. Компьютеры, например, используют двоичные числа для представления и обработки информации. Знание двоичной системы счисления позволяет нам лучше понимать и работать с компьютерами, а также различными алгоритмами и системами, основанными на цифровой логике.
Как представляются числа в двоичной системе счисления?
Когда мы представляем число в двоичном виде, мы можем расшифровать его путем умножения каждой цифры на 2 в соответствующей степени и сложения всех результатов. Например, число 1010, прочитанное как «десять» в десятичной системе, будет представлять 1*2^3 + 0*2^2 + 1*2^1 + 0*2^0 = 8 + 0 + 2 + 0 = 10.
Подобно десятичной системе, где каждая цифра имеет значение, в двоичной системе с каждым разрядом число умножается на степень двойки. Например, в числе 1010 первая единица относится к 2^3, вторая – к 2^2 и т.д. Следовательно, каждый разряд в числе имеет свое значение, которое прикреплено к соответствующей степени двойки.
В зависимости от количества битов или разрядов используют различные двоичные числа:
- 1 бит или разряд: представлен 0 или 1.
- 2 бита или разряда: представлены числами от 0 до 3 (00, 01, 10, 11).
- 3 бита или разряда: представлены числами от 0 до 7 (000, 001, 010, 011, 100, 101, 110, 111) и т. д.
Также существует стандартный способ представления отрицательных чисел в двоичной системе с помощью двоичного дополнения. В этом случае бит знака указывает на положительное или отрицательное число.
В двоичной системе счисления становится возможным выполнять все операции, такие как сложение, вычитание, умножение и деление, а также представлять десятичные числа. Она широко используется в компьютерах и информационных технологиях, где все данные хранятся и обрабатываются в двоичном коде.
Как представляется число 5 в двоичной системе счисления?
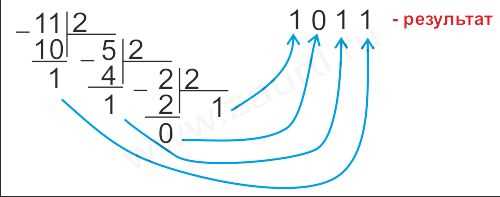
Чтобы представить число 5 в двоичной системе счисления, мы должны разложить его на сумму разрядных частей. Начинаем с наибольшей степени 2 и двигаемся влево, пока не достигнем степени 0.
Таким образом, число 5 в двоичной системе счисления может быть представлено следующим образом:
- Множитель 2^0 (наименьший разряд) — 1
- Множитель 2^1 — 0
- Множитель 2^2 — 1
Полученное число в двоичной системе счисления будет 101.
Таким образом, число 5 в двоичной системе счисления равно 101.
Примеры других чисел в двоичной системе счисления
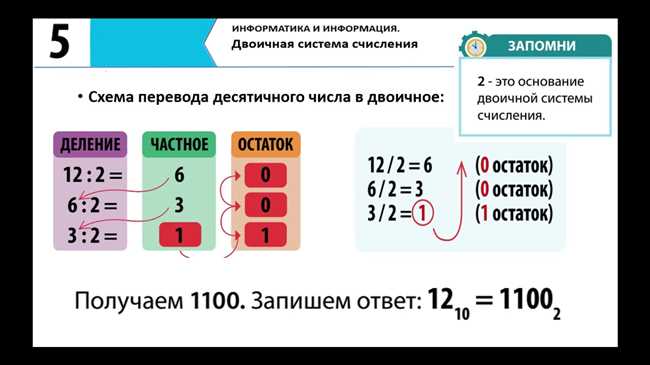
Вот несколько примеров чисел в двоичной системе счисления:
- Число 2: В двоичной системе счисления число 2 будет представлено как 10. Это означает, что у нас есть одна единица и ноль нулей.
- Число 3: Чтобы представить число 3 в двоичной системе счисления, мы должны написать 11. Это означает, что у нас есть две единицы и ноль нулей.
- Число 4: В двоичной системе число 4 будет записано как 100. Это означает, что у нас есть одна единица и два нуля.
- Число 6: Чтобы записать число 6 в двоичной системе счисления, мы должны написать 110. Это означает, что у нас есть одна единица, два нуля и ещё одна единица.
Таким образом, в двоичной системе счисления мы можем представлять разнообразные числа, используя только два символа.






