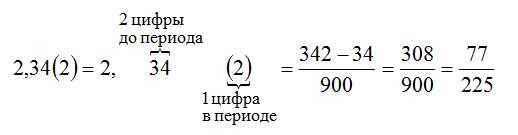
Как перевести десятичные числа в обыкновенные дроби? Этот процесс довольно прост, и я поделюсь с вами несколькими шагами, которые помогут вам справиться с этой задачей. Сначала нам нужно разобраться в структуре десятичного числа, чтобы легче его расшифровать. Затем мы используем числа до запятой, чтобы получить числитель дроби, и числа после запятой, чтобы получить знаменатель. Далее мы сокращаем полученную дробь, если это необходимо, и получаем итоговый результат. Важно помнить, что перевод десятичных чисел в обыкновенные дроби не всегда возможен, поэтому не стесняйтесь использовать калькулятор или другие инструменты для упрощения этого процесса.
Определение десятичных чисел
Компаниям ичастным лицам используют десятичные числа для представления данных о количестве, величинах, размерах, стоимости и других измеряемых характеристиках. Десятичные числа обычно записываются в виде цифр 0-9 и разделителями, такими как точка (.) или запятая (,). В зависимости от страны используется разный разделитель — в некоторых странах применяется запятая, а в других — точка.
Десятичные числа также могут быть положительными или отрицательными, в зависимости от значения, которое они представляют. Например, число 3,14 является положительным десятичным числом, а число -2,5 является отрицательным десятичным числом.
Определение десятичных чисел включает в себя понимание и использование разрядов после десятичной точки. В этих десятичных разрядах каждая цифра имеет свое значение в зависимости от ее положения. Например, в числе 3,14 цифра «3» находится в разряде единиц, цифра «1» — в разряде десятых, а цифра «4» — в разряде сотых.
Чтобы лучше понять, как десятичные числа работают, давайте рассмотрим следующий пример: если у нас есть число 2,345, то число «2» находится в разряде единиц, цифра «3» — в разряде десятых, цифра «4» — в разряде сотых и цифра «5» — в разряде тысячных. Каждый разряд имеет вес, который определяется его положением относительно десятичной точки.
Десятичные числа в повседневной жизни
Одной из наиболее распространенных областей, где десятичные числа используются, является финансовая сфера. Когда мы покупаем что-то в магазине, цена товара обычно указана с разделительной точкой и десятичной частью. Мы можем легко рассчитать итоговую сумму покупки, прибавив стоимость каждого товара. Также десятичные числа используются для расчета налогов, скидок, процентов и других финансовых операций.
Десятичные числа также широко применяются в науке и технике. Например, при измерении длины или массы предметов используются десятичные деления. Если мы хотим узнать, сколько килограммов весит какой-то предмет, то мы часто видим его массу, выраженную в десятичных единицах, например, 2,5 кг.
Десятичные числа также помогают нам в повседневных задачах, связанных с переводом единиц измерения. Если мы хотим перевести метры в километры, мы просто делим число на 1000. Также десятичные числа упрощают расчет времени. Например, если мы хотим узнать, сколько минут составляет полчаса, мы знаем, что это 30 минут или 0,5 часа.
Десятичные числа также используются в географии и навигации. Например, координаты места на Земле, выраженные в градусах, имеют десятичную форму. Это позволяет нам точно определить местоположение точек на карте или глобусе.
В общем, десятичные числа — это неотъемлемая часть нашей повседневной жизни. Они помогают нам совершать финансовые операции, измерять предметы и решать различные задачи. Без них наша жизнь была бы гораздо сложнее и менее организованной. Именно благодаря десятичным числам мы можем точно и легко работать с дробными и нецелыми значениями.
Десятичные числа в математике
Девятидесятипроцентных чисел легко понять и использовать, поскольку они связаны с нашей повседневной жизнью. Мы часто используем их для представления денежных сумм, измерения времени, расстояний и т.д. Например, 2,5 может означать 2 целых числа и 5 десятых, 0,75 — 0 целых чисел, 7 десятых и 5 сотых, а 1,25 — 1 целое число, 2 десятых и 5 сотых.
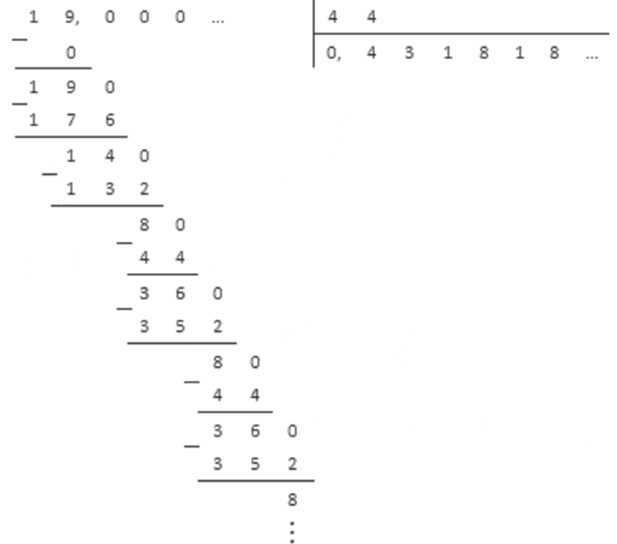
Десятичные числа также могут быть как конечными, так и бесконечными. Конечные десятичные числа имеют ограниченное число десятичных разрядов, например, 3,14 или 0,5. Бесконечные десятичные числа имеют бесконечное количество десятичных разрядов и могут повторяться или быть неповторяющимися, например, 0,3333… или 1,41421356…
Перевод десятичных чисел в обыкновенные дроби — это процесс, который позволяет представить десятичное число в виде дроби. Можно использовать различные методы для перевода десятичных чисел в дроби, такие как десятичная дробь, десятичная группа или десятичная цепь. Эти методы позволяют нам легко работать с десятичными числами и решать математические задачи, связанные с ними.
Суммируя, десятичные числа являются важным аспектом математики и повседневной жизни. Они позволяют нам работать с точностью и удобством, представлять различные величины и решать разнообразные задачи. Понимание десятичных чисел полезно для нашего интеллектуального развития и позволяет нам лучше понимать мир вокруг нас.
Принцип перевода десятичных чисел в обыкновенные дроби
Представление десятичных чисел в виде обыкновенных дробей может быть полезным как в повседневной жизни, так и в математике. Преобразование десятичного числа в обыкновенную дробь основывается на принципе разложения числа на целую и десятичную части.
Для начала, давайте рассмотрим для примера число 3,25. Чтобы перевести это число в обыкновенную дробь, мы разделим его на его целую часть и десятичную часть. В данном случае, 3 будет целой частью, а 0,25 — десятичной.
Сначала преобразуем десятичную часть в дробь. Для этого, в числителе будет цифры десятичной части (25), а в знаменателе будет число 10, возведенное в степень, равную количеству цифр в десятичной части (2). Таким образом, мы получим дробь 25/100.
Теперь объединим целую часть и дробную часть. Чтобы это сделать, умножим целую часть на знаменатель дроби десятичной части (10), а затем прибавим числитель дроби десятичной части (25). В нашем примере, это будет 3 * 10 + 25 = 30 + 25 = 55.
Итак, число 3,25 в обыкновенной дроби равно 55/100.
- Делаем общий знаменатель, если необходимо. Если дробь уже идеальна и не может быть сокращена, то у вас уже есть обыкновенная дробь. Но если знаменатели дробей отличаются, необходимо привести их к общему знаменателю. Для этого умножаем каждую дробь на такое число, чтобы знаменатель всех дробей был одинаковым.
- Сложите или вычтите числители. После приведения дробей к общему знаменателю, мы можем сложить или вычесть числители. Знаменатель остаётся неизменным.
- Упростить полученную дробь. После проведения операций с числителями можно упростить дробь, если это возможно. Если числитель и знаменатель имеют общие делители, их можно сократить.
Теперь, когда вы знаете принцип перевода десятичных чисел в обыкновенные дроби, вы можете использовать этот метод для удобства в повседневной жизни или в математических расчетах. Ключевым моментом является разложение числа на целую и десятичную части, а затем преобразование десятичной части в дробь. Не забудьте упростить полученную дробь, если это возможно.
Основные шаги для перевода десятичных чисел в обыкновенные дроби
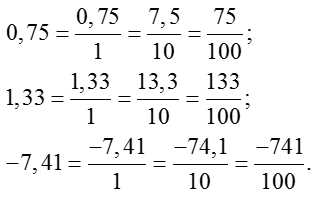
Перевод десятичных чисел в обыкновенные дроби может показаться сложным процессом на первый взгляд, но на самом деле он не так уж и сложен. С помощью нескольких основных шагов вы сможете легко и точно выполнить эту операцию. Давайте рассмотрим эти шаги подробнее.
Шаг 1: Разделите число на его целую и десятичную части. Например, если у вас есть число 3.45, то его целая часть равна 3, а десятичная часть равна 0.45.
Шаг 2: Переведите десятичную часть числа в обыкновенную дробь без изменения её значения. Если у вас есть число 0.45, то это можно записать как 45/100.
Шаг 3: Сократите обыкновенную дробь, если это возможно. В данном примере, 45/100 можно сократить до 9/20, разделив числитель и знаменатель на их наибольший общий делитель, который в данном случае равен 5.
Шаг 4: Объедините целую часть числа с обыкновенной дробью, чтобы получить окончательный результат. В данном примере, число 3.45 можно записать в виде обыкновенной дроби 3 9/20, где 3 — это целая часть, а 9/20 — это десятичная часть, переведенная в обыкновенную дробь.
Теперь, когда вы знакомы с основными шагами для перевода десятичных чисел в обыкновенные дроби, вы можете применить эти шаги к любому десятичному числу и получить его эквивалент в виде обыкновенной дроби. Важно помнить, что сокращение обыкновенной дроби является ключевым шагом этого процесса, поскольку он помогает упростить результат и сделать его более точным.
Примеры перевода десятичных чисел в обыкновенные дроби
В данной статье мы рассмотрели несколько примеров перевода десятичных чисел в обыкновенные дроби. Этот метод очень полезен при работе с десятичными числами и может быть применен в различных ситуациях.
В первом примере мы рассмотрели перевод десятичного числа 0.25 в обыкновенную дробь. Мы увидели, что 0.25 может быть представлена в виде дроби 1/4.
Во втором примере мы рассмотрели перевод десятичного числа 0.5 в обыкновенную дробь. Здесь мы увидели, что 0.5 эквивалентно дроби 1/2.
В третьем примере было рассмотрено перевод десятичного числа 0.75 в обыкновенную дробь. Установили, что 0.75 может быть записано в виде дроби 3/4.
Эти примеры помогли нам разобраться в основном принципе перевода десятичных чисел в обыкновенные дроби. Однако, стоит отметить, что есть и другие методы и правила перевода, которые могут быть использованы в зависимости от сложности чисел и требуемой точности.
В целом, перевод десятичных чисел в обыкновенные дроби является важной математической операцией, которая помогает нам работать с числами в различных контекстах. Это навык, который может быть полезен в повседневной жизни, работе и образовании.






