
Перевод чисел из одной системы счисления в другую — довольно распространенная и полезная задача в математике и программировании. В частности, если вам нужно перевести число из десятичной системы счисления в троичную, существует несколько способов делать это. Один из самых простых способов — использовать деление с остатком. Этот метод заключается в последовательном делении числа на основание новой системы счисления (в данном случае, на 3) и записи остатков от деления. Повторяя этот процесс до тех пор, пока число не станет равным нулю, мы получаем троичное представление исходного числа. Другой метод — использование алгоритма с помощью битовых операций, позволяющего более эффективно выполнять перевод числа из одной системы счисления в другую.
Шаг 1: Определение цифр троичной системы числения
Перед тем как мы перейдем к переводу числа из десятичной системы в троичную, давайте разберемся, из каких цифр состоит сама троичная система числения.
В троичной системе используются всего три цифры: 0, 1 и 2. Эти цифры представляют различные значения, аналогичные цифрам 0-9 в десятичной системе. Однако, в троичной системе их значения немного отличаются.
Значение цифры 0 в троичной системе остается таким же, как и в десятичной системе. Оно представляет собой отсутствие единиц и имеет значение «ноль».
Цифра 1 в троичной системе означает наличие одной единицы и имеет значение «один».
А цифра 2 в троичной системе означает наличие двух единиц и имеет значение «два».
Принципиальное отличие троичной системы от десятичной заключается в том, что их базы различны. В десятичной системе база равна 10, так как используются 10 цифр (от 0 до 9). В троичной системе база равна 3, так как используются только 3 цифры (0, 1 и 2).
Понимание этих цифр и их значений в троичной системе является ключевым для перевода чисел из десятичной системы в троичную. Следующим шагом будет разбор процесса перевода конкретного числа. Теперь, когда у нас есть понимание цифр троичной системы числения, перейдем к следующему шагу.
Что такое троичная система?
Основание системы счисления указывает, сколько разрядов может принимать каждая позиция числа. В десятичной системе позиции могут принимать значения от 0 до 9, в двоичной — от 0 до 1, а в троичной — от 0 до 2.
В троичной системе числа образуются путем комбинирования трех цифр: 0, 1 и 2. Начиная с младшего разряда, каждый следующий разряд имеет вес, увеличенный в 3 раза по сравнению с предыдущим разрядом. Таким образом, число 102 в троичной системе равно: 1 * 3^2 + 0 * 3^1 + 2 * 3^0 = 9 + 0 + 2 = 11 в десятичной системе.
Троичная система счисления широко применяется в информатике для представления данных с более экономичным использованием памяти и упрощением операций. Она также может использоваться для решения математических задач и в различных научных областях.
Троичная система имеет свои особенности и связана с троичной логикой, которая используется в компьютерных системах и при разработке цифровых схем.
Какие цифры используются в троичной системе числения?

Первая цифра, 0, обозначает отсутствие единиц в данной позиции числа. Вторая цифра, 1, обозначает наличие одной единицы, а третья цифра, 2, обозначает наличие двух единиц. Используя только эти три цифры, можно представить любое троичное число.
Например, число 10 в троичной системе означает 1 единицу и 0 двоек, что равно 3 в десятичной системе. А число 1112 в троичной системе означает 1 единицу, 1 двойку и 2 тройки, что равно 16 в десятичной системе.
Троичная система числения может использоваться в различных областях, таких как компьютерные науки, кодирование и телекоммуникации. В компьютерных приложениях троичные числа могут быть использованы для хранения и обработки данных с большей эффективностью по сравнению с десятичными числами.
Таким образом, троичная система числения использует только три цифры — 0, 1 и 2, и может быть использована для представления чисел в различных областях, от компьютерных наук до обыденной жизни.
Как преобразовать числа от 0 до 2 в троичной системе?
Для того чтобы преобразовать числа от 0 до 2 в троичной системе, нам потребуется понимание основ этой системы счисления. В троичной системе используются только три цифры: 0, 1 и 2. Как и в десятичной системе, каждая позиция числа в троичной системе имеет свою весовую стоимость, причем стоимость увеличивается в три раза при переходе справа налево.
- Число 0 в троичной системе обозначается цифрой 0. Оно не имеет никакого веса и является начальным значением.
- Число 1 в троичной системе обозначается цифрой 1. Оно имеет вес, равный 1, так как оно находится в первой позиции справа.
- Число 2 в троичной системе обозначается цифрой 2. Оно имеет вес, равный 3, так как оно находится во второй позиции справа.
Теперь у нас есть все необходимые сведения, чтобы преобразовать числа от 0 до 2 в троичной системе. Например, если нам нужно перевести число 2 в десятичной системе в троичную систему, мы просто записываем его как 2 и получаем ответ. А если мы хотим перевести число 1, то записываем его как 1. И, наконец, если мы хотим перевести число 0, записываем его как 0. Просто так, без изменений.
Троянская система является одной из основных систем счисления и используется во многих областях науки, техники и информатики. Понимание того, как переводить числа в троичную систему, может быть полезным при работе с более сложными проблемами и задачами, связанными с этой системой числения.
Шаг 2: Разбиение числа на разряды
Теперь, когда вы уже поняли, как работает троичная система счисления, пришло время узнать, как разбить число на разряды, чтобы перевести его из десятичной системы в троичную. Этот шаг необходим для того, чтобы упростить процесс перевода и сосредоточиться на каждой части числа по отдельности.
Для начала, представьте, что у вас есть число 235. Чтобы разбить его на разряды, нужно сначала понять, какой будет самый высокий разряд. В троичной системе это будет разряд единиц, затем разряд троек, разряд девяток и т.д. Определите, до какого разряда вы хотите представить число в троичной системе.
| Разряд | Позиция | Разряд в троичной системе |
|---|---|---|
| единиц | 1 | 2 |
| троек | 10 | 1 |
| девяток | 100 | 0 |
В нашем примере, если мы хотим представить число 235 в троичной системе, нам понадобятся разряды единиц, троек и девяток. Разбив число на эти разряды, получим:
- Разряд единиц: 235 % 3 = 2
- Разряд троек: (235 / 3) % 3 = 1
- Разряд девяток: (235 / 9) % 3 = 0
Заметьте, что для каждого разряда мы применяем разные операции, чтобы определить значение этого разряда в троичной системе. Для разряда единиц мы просто берем остаток от деления числа на 3, для разряда троек мы берем остаток от деления числа на 3, а затем делим на 3, чтобы получить новое число для дальнейших вычислений, и для разряда девяток мы берем остаток от деления числа на 9, а затем делим на 3.
Теперь, когда мы разбили число на разряды и определили значения для каждого разряда в троичной системе, мы готовы перейти к следующему шагу — записи числа в троичной системе.
Что такое разряд числа?
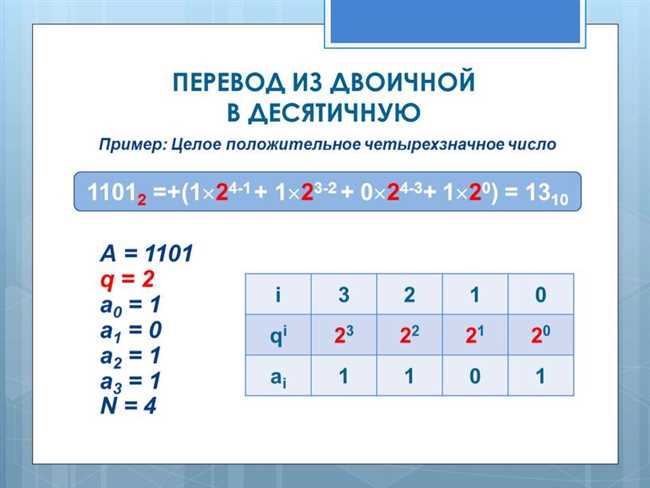
Давайте рассмотрим пример, чтобы лучше понять, что такое разряд числа в контексте десятичной системы. Возьмем число 135. В этом числе первый разряд (единицы) имеет вес 1, второй разряд (десятки) имеет вес 10, а третий разряд (сотни) имеет вес 100. Таким образом, можно представить число 135 как 1*100 + 3*10 + 5*1.
Разряд числа имеет большое значение при выполнении различных операций, таких как сложение, вычитание, умножение и деление. При сложении или вычитании двух чисел, алгоритм работает от младшего (маленького) разряда к старшему (большому) разряду. При умножении и делении также используются разные разряды для расчетов.
Очень важно понимать, что значения разрядов в системе счисления зависят от основания этой системы. В десятичной системе счисления значения разрядов варьируются от 0 до 9, поскольку она основана на числе 10. В двоичной системе счисления разряды могут иметь значения только 0 или 1, так как она основана на числе 2.
Вот некоторые особенности и факты о разрядах чисел:
- Младший разряд — это самый правый разряд в числе, а старший разряд — самый левый разряд. Например, в двоичном числе 1010, самый правый разряд имеет вес 2^0, а самый левый разряд имеет вес 2^3.
- Число разрядов в числе зависит от его значимости. Чем больше число, тем больше разрядов оно будет иметь. Например, число 3456 имеет 4 разряда, в то время как число 7 имеет только 1 разряд.
- Когда переводим число в другую систему счисления, его разряды также изменяются. Например, при переводе числа из десятичной системы счисления в двоичную, каждый разряд будет иметь только значения 0 или 1.
Заключение
Мы изучили различные способы разбиения числа на разряды, в том числе разбиение по десятичной системе счисления и разбиение по троичной системе счисления. Каждый из этих способов имеет свои особенности и применяется в различных ситуациях.
Важно помнить, что разбиение числа на разряды — это лишь первый шаг в работе с числами. Далее необходимо уметь обрабатывать каждый разряд отдельно, выполнять необходимые вычисления и анализировать полученные результаты.






