Раздел 1: Основные понятия

В нашем обычном, повседневном мире мы используем десятичную систему счисления, основанную на числе 10. Это значит, что мы имеем десять различных цифр — от 0 до 9, и когда мы составляем числа, мы можем использовать эти цифры в разных комбинациях. Например, число 27 состоит из цифр 2 и 7, что означает 2 десятичные доли и 7 единиц.
Однако существуют и другие системы счисления, такие как двоичная, в которой основанием является число 2. В двоичной системе счисления у нас есть только две цифры — 0 и 1. Представьте себе, как было бы интересно понимать и использовать эту систему!
Что такое двоичные числа? Это числа, которые можно представить с помощью только двух цифр — 0 и 1. Когда мы составляем двоичное число, мы можем использовать эти цифры в различных комбинациях, так же, как в десятичной системе счисления.
Пример:
Давайте рассмотрим число 5 и переведем его в двоичную систему счисления. В десятичной системе счисления это число состоит из одной пятерки. Но как это представить в двоичной системе?
Чтобы перевести число 5 в двоичное число, мы должны разделить его на два и записать остаток. Затем мы берем результат от деления и снова делим его на два, записывая остаток. Продолжаем этот процесс до тех пор, пока результат от деления не станет равным нулю.
Начнем:
- 5 ÷ 2 = 2, остаток 1
- 2 ÷ 2 = 1, остаток 0
- 1 ÷ 2 = 0, остаток 1
Значение числа в двоичной системе счисления определяется снизу вверх, начиная с остатка последнего деления. В результате получаем число 101.
Вот и все! Вы только что научились переводить число 5 в двоичную систему счисления. Впечатляюще, не так ли? И это было только начало!
Раздел 2: Двоичная система счисления
Когда мы говорим о числе 5 в двоичной системе счисления, мы должны представить его в виде комбинации «0» и «1». В двоичной системе счисления каждая цифра в числе имеет определенное значение, в зависимости от ее позиции. Например, в числе 10101, первая позиция справа обозначает 2^0, вторая позиция обозначает 2^1, третья позиция обозначает 2^2 и так далее.
Теперь, когда мы знаем, какие значения представляют каждую позицию в двоичной системе счисления, давайте рассмотрим, как перевести число 5 в двоичную систему.
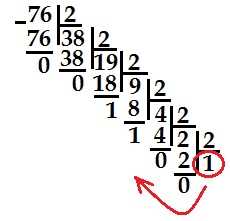
Чтобы перевести число 5 в двоичную систему счисления, мы должны делить его на 2 и записывать остатки от деления в обратном порядке. Продолжаем делить полученные частные на 2 до тех пор, пока не получим нулевое частное. Это называется делением в столбик.
1. Делим 5 на 2: 5 ÷ 2 = 2 и остаток 1. Записываем остаток 1.
2. Делим 2 на 2: 2 ÷ 2 = 1 и остаток 0. Записываем остаток 0.
3. Делим 1 на 2: 1 ÷ 2 = 0 и остаток 1. Записываем остаток 1.
Таким образом, число 5 в двоичной системе счисления будет выглядеть как 101.
Вот и все! Теперь вы знаете, как перевести число 5 в двоичную систему счисления. Попробуйте сами перевести другие числа в эту систему и исследовать магию двоичных чисел!
Раздел 3: Перевод числа 5 в двоичную систему счисления
Теперь, когда мы понимаем, что такое двоичная система счисления и имеем представление о ее основах, настало время разобраться, как перевести число 5 в двоичную систему.
Когда мы говорим о переводе числа 5 в двоичную систему счисления, мы должны учесть, что двоичная система имеет только две цифры – 0 и 1. Поэтому, чтобы перевести число 5 в двоичную систему, мы должны найти комбинацию цифр 0 и 1, которая будет представлять данное число.
Существует несколько способов перевода числа в двоичную систему счисления, но мы рассмотрим простой и понятный метод, который основан на делении числа на 2.
Итак, начнем:
- Начните с числа 5 и разделите его на 2. В результате получится частное 2 и остаток 1.
- Далее, разделите частное 2 на 2. Снова получите частное 1 и остаток 0.
- Продолжайте делить частное на 2 до тех пор, пока не получите частное равное 0.
- Запишите все остатки, начиная с последнего остатка, полученного на первом шаге: 101.
Таким образом, число 5 в двоичной системе счисления представляется как 101.
Важно помнить, что перевод числа в двоичную систему счисления может потребовать нескольких итераций. Иногда это может быть сложной задачей, особенно при работе с более сложными числами.
Однако с практикой у вас обязательно получится, и вы сможете легко переводить числа в двоичную систему счисления. Постепенно ваш мозг привыкнет к алгоритму перевода и сможет автоматически применять его при необходимости.
Раздел 4: Проверка правильности перевода
Для проверки правильности перевода числа 5 в двоичную систему счисления мы можем воспользоваться следующими методами:
- Сравнить результат с таблицей перевода. В нашем случае, перевод числа 5 в двоичную систему дает значение 101. Сравнив результат с таблицей, мы можем убедиться, что перевод выполнен правильно.
- Выполнить обратный перевод. Мы можем взять полученное двоичное число 101 и выполнить обратную операцию, переводя его в десятичную систему счисления. Если результат будет равен исходному числу 5, то мы можем быть уверены в правильности перевода.
Благодаря выполнению данных шагов, мы можем убедиться в правильности перевода числа 5 в двоичную систему счисления и быть уверенными, что результаты наших вычислений являются точными и достоверными.






