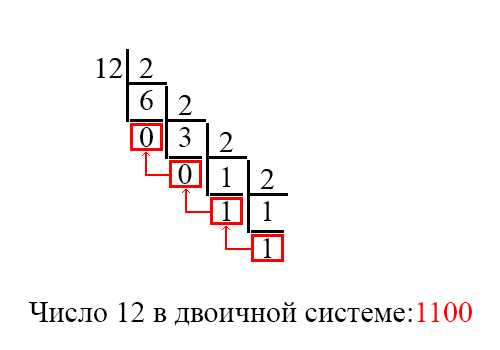
Если тебя интересует, как перевести число 27 в двоичную систему счисления, то давай разберемся. Двоичная система основана на использовании только двух цифр — 0 и 1, в отличие от десятичной системы, которую мы обычно используем в повседневной жизни. Чтобы перевести 27 в двоичную систему, нужно разделить его на 2 и записать остаток. Затем этот остаток нужно записать в обратном порядке, чтобы получить двоичное представление числа.
Применяя этот алгоритм к числу 27, мы получим результат в виде «11011». Значение последнего остатка будет самым левым битом (1), а значение первого остатка будет самым правым битом (1). Это даст нам двоичное представление числа 27.
Теперь ты знаком с секретами преобразования числа 27 в двоичную систему счисления. Приложи этот метод и к другим числам, чтобы овладеть навыком перевода чисел в двоичную систему и расширить свои математические знания. Удачи!
Что такое двоичная система счисления?
Основное преимущество двоичной системы счисления заключается в том, что она проста для понимания и обработки компьютерами. Все числа в компьютере представляются в виде двоичных значений, так как электрический ток может принимать два состояния: включенный (1) и выключенный (0). Бинарные значения используются для хранения информации и выполнения вычислений.
В двоичной системе счисления каждая цифра имеет свое место и весовой коэффициент. Первая цифра слева имеет вес, равный 2^0, вторая имеет вес, равный 2^1, третья — вес 2^2, и так далее.
Для примера, давайте рассмотрим число 27. Чтобы перевести его в двоичную систему счисления, мы должны разделить 27 на 2 и записать частное и остаток. Затем продолжим деление остатка на 2 и так далее, пока не достигнем нулевого частного.
Вот таблица с промежуточными значениями в процессе перевода числа 27 в двоичную систему счисления:
| Деление на 2 | Частное | Остаток (цифра в двоичном числе) |
|---|---|---|
| 27 | 13 | 1 |
| 13 | 6 | 0 |
| 6 | 3 | 0 |
| 3 | 1 | 1 |
| 1 | 0 | 1 |
Итак, число 27 в двоичной системе счисления будет записываться как 11011.
Двоичная система счисления широко используется в компьютерной науке, информатике и электронике. Понимание и использование двоичной системы счисления помогает понять принципы работы компьютеров и других электронных устройств. Кроме того, знание двоичной системы счисления может быть полезно при решении некоторых математических задач и в других областях науки и техники.
Таким образом, двоичная система счисления — это простая и эффективная система представления чисел, основанная на использовании всего двух цифр 0 и 1. Она играет важную роль в различных областях, связанных с компьютерами и электроникой, и позволяет нам лучше понять работу современных технологий и их принципы.
Шаг 1: Разделение числа на степени двойки
Для начала, давайте разберемся, как перевести числа из десятичной системы счисления в двоичную. Чтобы это сделать, нам необходимо разбить число на степени двойки.
Возьмем, например, число 27. Сейчас его десятичное значение, но мы хотим преобразовать его в двоичное.
Спрашивается, какие степени двойки мы используем для этого перевода? Начнем с самой маленькой степени, то есть единицы (2^0). Затем пройдемся по возрастающим степеням двойки: 2^1, 2^2, 2^3 и так далее.
| Степень двойки | Удельное значение | Целая часть | Остаток |
|---|---|---|---|
| 2^0 | 1 | 27 | 0 |
| 2^1 | 2 | 13 | 1 |
| 2^2 | 4 | 6 | 0 |
| 2^3 | 8 | 3 | 1 |
| 2^4 | 16 | 1 | 1 |
| 2^5 | 32 | 0 | 1 |
Как только число станет меньше или равно 0, мы заканчиваем. В данном случае, как только мы получим 0 в целой части, переходим к остатку.
Таким образом, число 27 в двоичной системе будет выглядеть как 11011.
Теперь вы знаете первый шаг в преобразовании числа из десятичной системы в двоичную. Продолжайте практиковаться, и скоро вы сможете выполнять это быстро и легко!
Шаг 2: Определение битов
Биты — это основа двоичной системы счисления и представляют собой двоичные цифры 0 и 1. Каждый бит имеет определенное место в числе и влияет на его значение.
Для перевода числа 27 в двоичную систему счисления, нам необходимо разбить его на биты. Обычно мы начинаем с наибольшего разряда и движемся вниз по разрядам числа. В данном случае, у нас есть число 27, которое нужно представить в двоичной системе.
Вопрос: Какой разряд наиболее значимый в числе 27?
Ответ: Самый левый разряд, так как он представляет наибольшую степень числа 2.
| Разряд | Значение |
|---|---|
| 2^4 | 16 |
| 2^3 | 8 |
| 2^2 | 4 |
| 2^1 | 2 |
| 2^0 | 1 |
Когда мы определяем биты для числа 27, мы начинаем с наиболее значимого разряда, который равен 2^4, то есть 16. Если мы можем вычесть 16 из числа 27, то этот бит будет равен 1, в противном случае он будет равен 0. Мы продолжаем этот процесс для каждого разряда, пока не получим конечное двоичное представление числа 27.
Таким образом, наши биты для числа 27 будут: 11011. Это означает, что число 27 в двоичной системе равно 11011.
Шаг 3: Заполнение числа нулями

Чтобы заполнить число нулями, мы сначала определяем количество разрядов, которое мы хотим использовать для представления двоичного числа. Для примера, давайте сделаем предположение, что мы хотим представить число 27 в формате 8-разрядного двоичного числа.
После определения количества разрядов мы приступаем к заполнению пустых разрядов нулями слева от двоичного числа. В нашем случае, перед числом 27 должны быть добавлены нули в количестве 7, чтобы получить 8-разрядное двоичное число. Таким образом, 27 становится 00011011.






