- Перевод чисел в двоичную систему счисления
- Шаги для перевода числа в двоичную систему:
- Что такое двоичная система счисления?
- Перевод целых чисел в двоичную систему
- Перевод дробных чисел в двоичную систему
- Пример 1: Перевод десятичной дроби 0.625 в двоичную систему
- Пример 2: Перевод десятичной дроби 0.3 в двоичную систему
- Применение двоичной системы
Как перевести числа в двоичную систему: пошаговая инструкция и примеры
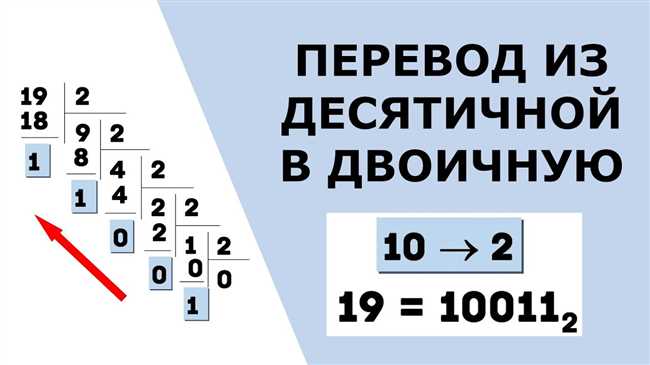
Вы наверняка слышали о двоичной системе, одной из основных систем счисления, применяемых в информатике и компьютерных науках. Но как перевести числа из десятичной или любой другой системы счисления в двоичную? В этой статье мы рассмотрим пошаговую инструкцию и дадим несколько примеров для ясности.
Перевод числа в двоичную систему основан на делении числа на 2 и записи остатков в обратном порядке. Этот процесс может показаться сложным на первый взгляд, но на самом деле он не такой уж и сложный. После прочтения данной статьи вы сможете без труда переводить числа в двоичную систему и понимать, как это работает.
Также мы приведем несколько примеров перевода чисел в двоичную систему, чтобы вы могли лучше понять, как применять эту инструкцию на практике. Готовы ли вы познакомиться с двоичной системой и научиться переводить числа? Поехали!
Перевод чисел в двоичную систему счисления
Для перевода числа из десятичной системы счисления в двоичную нужно последовательно делить число на 2 и записывать остатки от деления справа налево. Процесс прекращается, когда результат деления становится равным нулю.
Шаги для перевода числа в двоичную систему:
- Начните с числа, которое нужно перевести в двоичную систему.
- Поделите это число на 2.
- Запишите остаток от деления (0 или 1).
- Поделите результат предыдущего деления на 2.
- Запишите остаток от деления.
- Продолжайте делить и записывать остатки, пока результат деления не станет равным нулю.
- Запишите остатки в обратном порядке — справа налево, и получите двоичное представление числа.
Пример:
Рассмотрим пример перевода числа 42 в двоичную систему.
Шаг 1: Делим 42 на 2 получаем 21, остаток 0.
Шаг 2: Делим 21 на 2 получаем 10, остаток 1.
Шаг 3: Делим 10 на 2 получаем 5, остаток 0.
Шаг 4: Делим 5 на 2 получаем 2, остаток 1.
Шаг 5: Делим 2 на 2 получаем 1, остаток 0.
Шаг 6: Делим 1 на 2 получаем 0, остаток 1.
Обратный порядок остатков: 101010
Таким образом, число 42 в двоичной системе счисления представляется как 101010.
Не так уж сложно, верно? Теперь вы можете попробовать самостоятельно перевести любое число в двоичную систему счисления. Удачи со всеми ваши вычислениями!
Что такое двоичная система счисления?

Чтобы лучше понять, как работает двоичная система счисления, давайте рассмотрим пример: десятичное число 234. В десятичной системе степени десяти используются для определения значения каждой цифры на каждой позиции: сотни, десятки и единицы. Таким образом, число 234 можно разложить на сумму 2 * (10^2) + 3 * (10^1) + 4 * (10^0).
В двоичной системе счисления используются степени двойки. Например, число 1011 в двоичной системе счисления можно разложить на сумму: 1 * (2^3) + 0 * (2^2) + 1 * (2^1) + 1 * (2^0). В результате получаем число 11 в десятичной системе, потому что 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1 = 11.
Двоичная система счисления очень важна для компьютеров, потому что вся информация в компьютере хранится и обрабатывается в виде двоичных чисел, состоящих из набора нулей и единиц. Каждый символ, буква или число, является битом информации, и компьютер оперирует этими битами путем изменения их состояний.
- Двоичная система счисления имеет только два символа – 0 и 1.
- Каждая позиция числа в двоичной системе имеет значение, равное степени двойки.
- Информация в компьютере хранится и обрабатывается в двоичной форме.
Перевод целых чисел в двоичную систему
В двоичной системе счисления используются только две цифры: 0 и 1. Поэтому для перевода целых чисел в двоичную систему нужно разделить число на два и записывать остатки от деления. Этот процесс продолжается до тех пор, пока не достигнем нуля.
Давайте рассмотрим пример: десятичное число 23. Начинаем с деления:
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | |
| 11 | 1 | |
| 5 | 0 | |
| 2 | 1 | |
| 1 | 1 | |
| 0 |
Шаг 1: Делим 23 на 2, получаем остаток 1. Записываем его в первый столбец двоичного числа.
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | 1 |
| 11 | 1 | |
| 5 | 0 | |
| 2 | 1 | |
| 1 | 1 | |
| 0 |
Шаг 2: Делим полученное число (11) на 2, получаем остаток 1. Записываем его во второй столбец двоичного числа.
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | 1 |
| 11 | 1 | 1 |
| 5 | 0 | |
| 2 | 1 | |
| 1 | 1 | |
| 0 |
Шаг 3: Продолжаем деление для полученного числа (5) и получаем остаток 0. Записываем его в третий столбец двоичного числа.
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | 1 |
| 11 | 1 | 1 |
| 5 | 0 | 0 |
| 2 | 1 | |
| 1 | 1 | |
| 0 |
Шаг 4: Продолжаем деление для полученного числа (2) и получаем остаток 1. Записываем его в четвёртый столбец двоичного числа.
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | 1 |
| 11 | 1 | 1 |
| 5 | 0 | 0 |
| 2 | 1 | 1 |
| 1 | 1 | |
| 0 |
Шаг 5: Делаем последнее деление для полученного числа (1) и получаем остаток 1. Записываем его в пятый столбец двоичного числа.
| Десятичное число | Остаток | Двоичное число |
|---|---|---|
| 23 | 1 | 1 |
| 11 | 1 | 1 |
| 5 | 0 | 0 |
| 2 | 1 | 1 |
| 1 | 1 | 1 |
| 0 |
Таким образом, десятичное число 23 в двоичной системе равно 10111.
Теперь вы знаете, как перевести целые числа в двоичную систему счисления. Пробуйте применять этот метод к другим числам и открывайте для себя новые возможности!
Перевод дробных чисел в двоичную систему
Перевод дробных чисел в двоичную систему счисления может показаться сложным, но на самом деле все довольно просто. Давайте разберемся вместе!
Для начала, вспомним основные понятия двоичной системы. В двоичной системе числа представляются с помощью двух цифр — 0 и 1. Каждая цифра в двоичной системе имеет свое значение в зависимости от позиции, на которой она находится. Позиции начинаются справа и увеличиваются в степени двойки.
Теперь перейдем к переводу дробных чисел в двоичную систему. Для этого нам потребуется умножение числа на 2 и выделение его целой части. Результат целой части будет являться следующей цифрой двоичного числа. Затем прибавим значение целой части и продолжим умножение десятичной части на 2.
Продолжаем этот процесс до тех пор, пока десятичная часть не станет равной нулю или не будет найден периодический знак. Повторяющийся знак указывает на то, что число имеет бесконечную десятичную дробь в двоичной системе.
Теперь давайте рассмотрим примеры для лучшего понимания.
Пример 1: Перевод десятичной дроби 0.625 в двоичную систему
Шаг 1: Умножим 0.625 на 2: 0.625 * 2 = 1.25, целая часть равна 1.
Шаг 2: Умножим десятичную часть на 2: 0.25 * 2 = 0.5, целая часть равна 0.
Шаг 3: Умножим десятичную часть на 2: 0.5 * 2 = 1.0, целая часть равна 1.
Итак, результат перевода десятичной дроби 0.625 в двоичную систему будет равен 0.101.
Пример 2: Перевод десятичной дроби 0.3 в двоичную систему
Шаг 1: Умножим 0.3 на 2: 0.3 * 2 = 0.6, целая часть равна 0.
Шаг 2: Умножим десятичную часть на 2: 0.6 * 2 = 1.2, целая часть равна 1.
Шаг 3: Умножим десятичную часть на 2: 0.2 * 2 = 0.4, целая часть равна 0.
Шаг 4: Умножим десятичную часть на 2: 0.4 * 2 = 0.8, целая часть равна 0.
Шаг 5: Умножим десятичную часть на 2: 0.8 * 2 = 1.6, целая часть равна 1.
Шаг 6: Умножим десятичную часть на 2: 0.6 * 2 = 1.2, целая часть равна 1.
Итак, результат перевода десятичной дроби 0.3 в двоичную систему будет равен 0.0100110011(0011) (знаки 0011 повторяются).
Перевод дробных чисел в двоичную систему счисления может быть немного сложным на первый взгляд, но с помощью описанного выше метода вы сможете легко освоить эту технику. Используйте эти знания на практике и они станут для вас полезными инструментами в работе с двоичными числами.
Применение двоичной системы
Двоичная система имеет широкое применение в различных областях, особенно в информационных технологиях. Ее простота и эффективность делают ее незаменимой для работы с цифровыми данными.
Вот некоторые области, где применяется двоичная система:
- Компьютеры: Все цифровые вычисления в компьютерах основаны на двоичной системе. Все данные, такие как текст, изображения и звуки, переводятся в двоичный код и обрабатываются в виде последовательности битов.
- Сети и связь: Двоичная система используется для передачи данных по сети. Пакеты данных, такие как электронная почта, веб-страницы и видео, кодируются в двоичный формат и передаются через сеть в виде цифровых сигналов.
- Хранение данных: Двоичная система применяется для хранения данных на магнитных и оптических носителях, таких как жесткие диски и DVD-диски. Данные на этих носителях записываются в виде магнитных или оптических зарядов, которые могут иметь только два состояния, представляемых нулем и единицей.
- Криптография: Двоичная система играет важную роль в алгоритмах шифрования и дешифрования. В криптографии биты используются для представления ключей и шифрованных сообщений, обеспечивая безопасность и конфиденциальность данных.
- Логические операции: Двоичная система используется для выполнения логических операций, таких как AND, OR и XOR. Эти операции являются основой для работы сигналов в электронных системах и цифровых схемах.
Все эти области являются лишь некоторыми из примеров применения двоичной системы. Ее универсальность и простота делают ее неотъемлемой частью современных технологий и систем.






