Как перевести 1/3 в десятичную дробь 130: методика и примеры расчетов

Есть легкий и эффективный способ перевести обычную дробь 1/3 в десятичную дробь 130. Мы расскажем о серии простых шагов, чтобы разобраться в этом быстро и легко. Можно использовать алгоритм деления с остатком, который поможет нам разделить числитель на знаменатель. Таким образом, 1 будет делиться на 3, и мы получим десятичную дробь. Для удобства, мы можем использовать калькулятор, чтобы выполнить это вычисление и упростить процесс. Научитесь применять этот метод и вы сможете легко преобразовывать обычные дроби в десятичные.

Почему важно знать, как перевести 1/3 в десятичную дробь 130?

Во-первых, умение работать с десятичными дробями позволяет нам более точно и точно решать математические задачи и проблемы в различных областях жизни. Геометрия, физика, экономика, статистика — все эти области требуют знания и понимания десятичной формы чисел. Например, если мы хотим рассчитать долю чего-либо, знание, как перевести 1/3 в десятичную дробь, может быть очень полезным. Оно поможет нам точно определить долю и использовать эту информацию в решении задачи.

Во-вторых, знание, как перевести 1/3 в десятичную дробь, позволяет нам лучше понимать и представлять числа в обычной жизни. Например, когда мы видим цену на товар, которая выражена в виде десятичной дроби, мы легко можем оценить ее стоимость и принять решение, есть ли у нас достаточно денег для покупки. Точное понимание десятичной формы чисел также помогает нам быть более осведомленными потребителями и принимать более обоснованные финансовые решения.

В-третьих, знание того, как перевести 1/3 в десятичную дробь, помогает нам развивать наши когнитивные способности и логическое мышление. Этот процесс требует анализа, рассуждения и применения математических правил, что способствует развитию нашего умственного потенциала. Кроме того, наши умения в работе с дробными числами помогают нам в решении других сложных задач и проблем, требующих логического мышления и аналитического подхода.

В итоге, знание, как перевести 1/3 в десятичную дробь, дает нам не только возможность точно решать математические задачи, но также помогает нам лучше понимать и представлять числа, развивает наши умственные навыки и улучшает наши коммуникативные способности. Поэтому этот навык является неотъемлемой частью нашей математической грамотности и успешного функционирования в современном мире.

Основные понятия

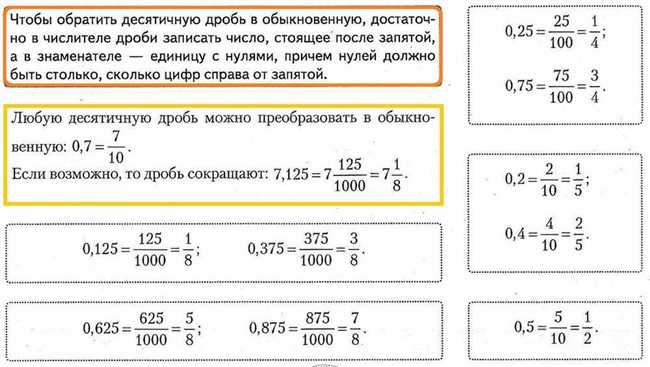
Прежде чем мы перейдем к вопросу о том, как перевести дробь 1/3 в десятичную форму, давайте разберемся с некоторыми основными понятиями, которые пригодятся нам в этом процессе.

Десятичная дробь

Десятичная дробь — это число, которое представлено в виде целой части и дробной части, разделенных запятой или точкой. Например, число 2,5 является десятичной дробью, где 2 — целая часть, а 5 — дробная часть.

Десятичные знаки и округление

Десятичные знаки — это цифры, которые идут после запятой или точки в десятичной дроби. Они показывают точность числа. Например, в числе 3,14159 есть пять десятичных знаков.

Округление — процесс, при котором число округляется до определенного количества десятичных знаков. Например, если мы округлим число 2,456 до двух десятичных знаков, получим число 2,46.

Перевод дроби в десятичную форму

Теперь давайте перейдем к вопросу, как перевести дробь 1/3 в десятичную форму. Для этого мы должны разделить числитель (1) на знаменатель (3). В данном случае, деление будет выглядеть следующим образом: 1 ÷ 3. Результатом этого деления будет неконечная десятичная дробь.

Теперь давайте попробуем разделить 1 на 3 и посмотрим, что получится:

Как видим, результатом деления 1 на 3 будет десятичная дробь с бесконечной последовательностью цифр 3. Такую десятичную дробь называют периодической десятичной дробью.

Теперь, когда мы знаем основные понятия и умеем переводить дробь 1/3 в десятичную форму, давайте приступим к решению других математических задач и расширим наши знания. Удачи!

Что такое десятичная дробь?

Десятичная дробь является одной из самых распространенных форм представления чисел и используется повсеместно в повседневной жизни. Она позволяет нам точно выражать части числа, которые меньше единицы.

Важно отметить, что десятичная дробь может быть конечной или бесконечной. Конечная десятичная дробь имеет конечное число цифр в десятичной части (например, 0.25), тогда как бесконечная дробь имеет повторяющийся или неповторяющийся цикл чисел в десятичной части (например, 0.333… или 0.142857142857…).

Десятичная дробь позволяет нам выполнить точные расчеты и измерения, так как она представляет собой универсальное и широко используемое представление чисел. Кроме того, она облегчает понимание отношений между различными частями числа и облегчает сравнение и сортировку чисел.

Что такое обыкновенная дробь?

Вы наверняка сталкивались с обыкновенными дробями в повседневной жизни. Например, когда вы делили пирог на части или считали доли в процентах. Обыкновенные дроби широко используются в различных областях, таких как математика, финансы, конструкция и т. д.

Одним из способов представления обыкновенной дроби является десятичная запись. Чтобы перевести обыкновенную дробь в десятичную, необходимо разделить числитель на знаменатель. Например, для дроби 1/3, мы делим 1 на 3 и получаем 0.33333…

Теперь давайте рассмотрим вопрос о том, как перевести 1/3 в десятичную дробь 130.

Пример перевода 1/3 в десятичную дробь

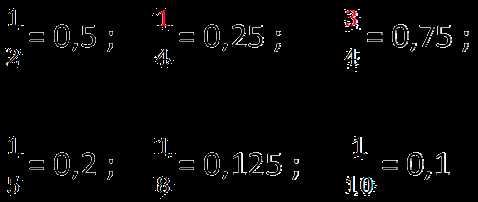
Давайте разберемся, как перевести обычную дробь 1/3 в десятичную форму. Это может показаться сложным для некоторых, но на самом деле это довольно просто.

Первый способ — деление. Делим числитель (1) на знаменатель (3). На самом деле, многие из нас уже знают ответ — это 0,33333… Но насколько точно это число и как его округлить?

Способ, который я предлагаю, поможет нам найти точное десятичное представление дроби 1/3 без округления. Для этого мы можем использовать постоянную десятичную дробь 0,3.

• Думайте об этом цифре: 0,3.
• Повторите ее два раза: 0,33.
• И снова повторите: 0,333.

Теперь у вас есть десятичная дробь 0,333, которая приближено равна 1/3. Она имеет ограниченное количество знаков после запятой, но мы можем сказать, что 1/3 близко к 0,333 без округления.

Таким образом, десятичное представление дроби 1/3 — это 0,333 (или 0,33, если нужно округлить до двух знаков).

Итак, мы рассмотрели пример перевода дроби 1/3 в десятичную дробь. Ответ — 0,333 (или 0,33). Независимо от того, для каких целей вам нужно это знать, я надеюсь, что этот пример помог вам разобраться!

Шаг 1: Разделение числа

Перед тем как приступить к переводу дроби в десятичную форму, давайте разберемся, как правильно разделить число.

Дробь 1/3 состоит из числителя и знаменателя. Числитель — это число, которое находится над чертой, в данном случае это 1. Знаменатель — число, которое находится под чертой, в данном случае это 3.

Возможный способ разделения дроби 1/3:

• Разделите числитель на знаменатель: 1 ÷ 3 = 0,333333333333333…

Итак, наша десятичная дробь будет равна 0,333333333333333…

Шаг 2: Деление числа

Представьте себе, что у вас есть одно яблоко, которое вы хотите разделить на 3 равные части. Как вы это сделаете? Вы разрежете яблоко на три равные части и получите три куска яблока. Таким образом, каждый кусок будет составлять одну третью от всего яблока. Точно так же и при делении числа на 3, мы разделяем его на три равные части.

Теперь перенесем это на практику. В задаче нам нужно перевести дробь 1/3 в десятичную дробь. Для этого мы можем разделить единицу на три.

1 ÷ 3 = 0.333333…

Как видите, результат деления является бесконечной десятичной дробью. Для удобства округлим его до трех знаков после запятой:

0.333

Таким образом, 1/3 в десятичной форме равно 0.333.

Убедитесь, что вы понимаете процесс деления и как получить десятичную дробь из обыкновенной. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в комментариях!

Заключение

Шаг 3: Округление числа

В данной статье мы рассмотрели как перевести обыкновенную дробь 1/3 в десятичную дробь. Однако, в некоторых случаях, результат может быть бесконечной десятичной дробью или иметь большое количество знаков после запятой. В таких случаях, для удобочитаемости и краткости, можно провести округление числа.

Округление числа позволяет сократить количество знаков после запятой и записать число с определенной точностью. Для округления числа следует учитывать следующее:

• Если первая цифра после запятой меньше 5 (включая 0), число округляется вниз до ближайшего меньшего целого числа.
• Если первая цифра после запятой больше 5, число округляется вверх до ближайшего большего целого числа.
• Если первая цифра после запятой равна 5, то число округляется до ближайшего четного целого числа.

Например, если результат перевода дроби 1/3 в десятичную форму равен 0.3333333333, мы можем округлить это число до 0.33 или 0.34, в зависимости от требуемой точности.

Округление числа упрощает его восприятие и удобно использовать в различных математических операциях. Однако, при округлении следует помнить о потере точности.