
Как определяется градусная мера дуги и как ее обозначают
Градусная мера дуги – это способ измерения угла между двумя лучами или сторонами. Она определяется путем деления окружности на 360 равных частей. Каждая такая часть называется градусом и обозначается символом «°».
Описание градусной меры дуги часто используется в геометрии, физике, астрономии и других науках, а также в повседневной жизни. Она позволяет измерять углы и устанавливать взаимное положение объектов.
Градусная мера дуги широко применяется в навигации, в технических спецификациях, в астрологии при определении положения планет и звезд, а также в картографии для обозначения направления или поворотов на карте. Важно понимать эту меру для точных измерений и точной ориентации в пространстве.
Что такое градусная мера дуги?
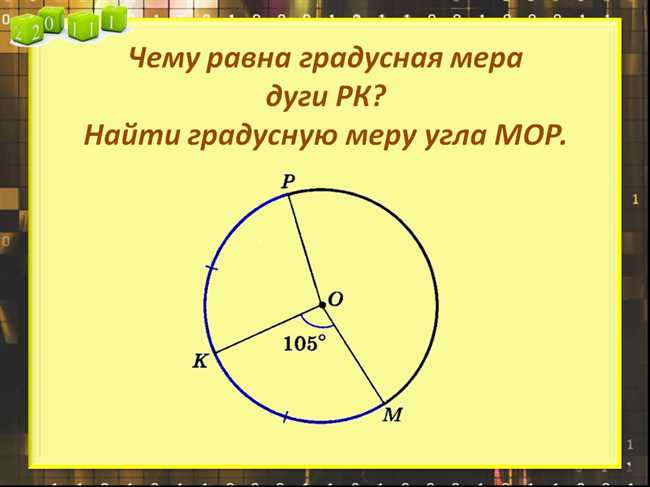
Когда мы говорим о градусной мере дуги, мы имеем в виду угловой размер, который занимает дуга на окружности. Так, если мы берем окружность и отмечаем на ней две точки, то дугу, соединяющую эти точки, можно измерить в градусах.
Например,представь себе круглую пиццу. Если я разделил ее на 8 равных частей и отметил две точки, то дуга, соединяющая эти точки, займет 45 градусов. Теперь представь, что я ему сказал тебе об этом и ты можешь легко представить, сколько долек пиццы займет та самая дуга.
- Градусная мера дуги является одним из наиболее распространенных способов измерения углов.
- В геометрии и тригонометрии градусы используются для измерения углов в плоскости.
- Кроме градусной меры, существуют и другие системы измерения углов, такие как радианы и грады.
- Радианы используются в математике и физике, а грады в геодезии и навигации.
Использование градусной меры дуги позволяет нам точно измерять и описывать углы в простом и понятном формате. Она широко применяется во множестве областей – от инженерии и архитектуры до астрономии и географии.
Так что, зная, что градусы представляют из себя единицу измерения угла, теперь ты можешь применить этот знак в своей повседневной жизни и развиваться в направлении, которое тебе интересно!
Как определить градусную меру дуги
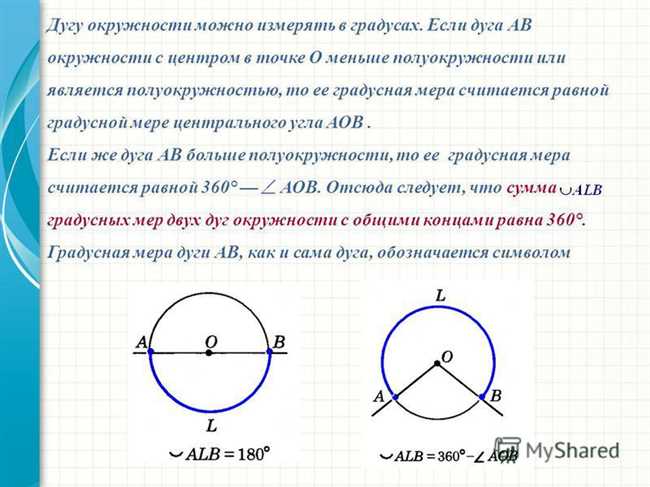
Если известна длина дуги и радиус окружности, градусная мера дуги может быть определена с помощью следующей формулы:
Градусная мера дуги = (Длина дуги / Длина окружности) * 360°
Например, предположим, что у нас есть дуга длиной 10 сантиметров, а радиус окружности составляет 5 сантиметров. Чтобы найти градусную меру этой дуги, мы используем формулу:
(10 см / 31,42 см) * 360° = 114,59°
Таким образом, градусная мера данной дуги составляет около 114,59°.
Важно отметить, что длина окружности может быть рассчитана с помощью формулы:
Длина окружности = 2π * Радиус
где π (пи) — математическая константа, приблизительно равная 3,14159 (как правило, округляется до 3,14).
С использованием таких формул и измерений, градусная мера дуги может быть точно определена.
Знание градусной меры дуги важно в различных областях, таких как астрономия, навигация, инженерия и даже в повседневной жизни. Это помогает определить углы поворота, разницу во времени и многое другое. Понимание того, как определить градусную меру дуги, дает нам возможность более полно и точно анализировать и изучать окружающий мир.
Обозначение градусной меры дуги
Обозначение градусной меры дуги часто производится символом «°». Например, чтобы обозначить угол, равный 45 градусам, мы пишем 45°. Этот символ добавляется после числового значения угла и является общепринятым способом обозначения градусов.
- Вместе с символом градусов, можно также указывать однозначное направление угла, используя символы «>» или «<". Например, 45° может быть обозначено как "45°>«, чтобы указать, что вращение происходит против часовой стрелки, или «45°<", чтобы указать, что вращение происходит по часовой стрелке.
- Если угол превышает 180 градусов, то используется дополнительное обозначение — символ «°». Например, угол в 270 градусов будет обозначаться как 270°.
Использование градусной меры дуги и ее обозначение позволяют нам точно измерять и описывать углы в пространстве. Это важный инструмент для многих научных и инженерных областей и помогает нам лучше понять и визуализировать углы вокруг нас.






