Как определить угол по его тангенсу на калькуляторе: подробная инструкция и примеры вычислений

Как вычислить угол, зная его тангенс на калькуляторе: подробная инструкция

Определение тангенса угла

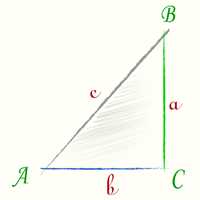
Итак, давайте подробнее разберемся, как определить тангенс угла. Для этого мы должны знать длины противоположего и прилежащего катетов в прямоугольном треугольнике.

Примем, например, угол A в прямоугольном треугольнике ABC. Если мы знаем длину катета AC (прилежащий катет) и длину катета AB (противоположный катет), то мы можем определить тангенс угла A по следующей формуле:

tg(A) = AB / AC

Если у нас есть значение тангенса угла A, мы можем использовать обратную функцию тангенса (арктангенс) для определения самого угла. Например, если мы знаем tg(A), мы можем вычислить угол A следующим образом:

A = arctg(tg(A))

Таким образом, зная длины противоположего и прилежащего катетов в прямоугольном треугольнике, мы можем определить тангенс угла и наоборот, зная значение тангенса угла, мы можем определить сам угол.

Теперь, когда вы знаете, как определить тангенс угла, вы можете использовать этот знакомый математический инструмент для решения разнообразных задач и применений, связанных с треугольниками, прямыми углами и другими тригонометрическими функциями.

Использование калькулятора для нахождения тангенса угла

Вы наверняка слышали о тангенсе угла, но возможно у вас есть вопрос, как его вычислить, используя калькулятор. Не волнуйтесь, я расскажу вам об этом подробнее.

Прежде чем приступить к вычислениям, убедитесь, что ваш калькулятор включен и находится в режиме работы с тригонометрическими функциями. Обычно калькуляторы имеют такие функции, как sin, cos и tan, которые соответствуют синусу, косинусу и тангенсу угла. Ваша цель — найти тангенс угла.

Перед вами стоит задача найти тангенс угла. Для этого следуйте инструкциям:

1. Введите значение угла, для которого нужно найти тангенс.
2. Нажмите кнопку с функцией тангенса (tan) на вашем калькуляторе.
3. После нажатия кнопки, калькулятор выведет значение тангенса угла.

Для большей точности, убедитесь, что ваш калькулятор находится в режиме работы с градусами (°). В некоторых моделях калькуляторов можно переключаться между режимами градусов, радианов и градов. Проверьте, что у вас выбран нужный режим перед вводом значения угла.

Теперь можно приступить к решению задачи. Вводите значения и находите тангенс угла с помощью калькулятора. Например, если вам нужно найти тангенс угла в 45 градусов, то введите значение 45 и нажмите кнопку с функцией тангенса. Калькулятор выдаст вам результат, который будет являться тангенсом данного угла.

Это очень полезный инструмент для вычислений в геометрии, физике, строительстве и других областях науки и техники, где вам часто приходится работать с углами. Теперь, когда вы знаете, как использовать калькулятор для нахождения тангенса угла, вы можете легко решать подобные задачи и делать свою работу более эффективной.

И не забывайте, что калькулятор — всего лишь инструмент, а самое главное — ваше понимание и знание математики. Калькулятор поможет вам получить ответы, но вы должны знать, как правильно использовать его и интерпретировать полученные результаты.

Нахождение угла по известному тангенсу на калькуляторе

Вы когда-нибудь сталкивались с ситуацией, когда вам нужно было вычислить угол, но у вас было только значение его тангенса? Не беспокойтесь, вы не одни. Многие люди испытывают трудности в поиске правильного решения в данной ситуации. В этом контексте я поделюсь с вами подробной инструкцией, которая поможет вам вычислить угол, зная его тангенс на калькуляторе.

Перед тем, как перейти к инструкции, давайте вспомним, что такое тангенс. Тангенс угла — это отношение противолежащего катета к прилежащему катету прямоугольного треугольника. Он вычисляется как отношение синуса косинуса угла. В математической нотации тангенс обозначается как tg.

Итак, как же можно вычислить угол при известном его тангенсе? Для этого вам потребуется использовать обратную функцию тангенса на калькуляторе. Эта функция обозначается как arctan или tan^-1. Чтобы вычислить угол, вам необходимо:

1. Возьмите калькулятор и найдите функцию arctan или tan^-1.
2. Введите значение тангенса, известное вам. Например, если вам известно, что tg угла равен 0,5, введите это значение в калькуляторе.
3. Нажмите кнопку, соответствующую функции arctan или tan^-1. Калькулятор выдаст результат, который будет являться значением угла, соответствующего заданному тангенсу.

Например, предположим, что вам известно, что tg угла равен 0,5. Выполнив вышеописанные шаги на калькуляторе, вы получите значение угла, соответствующее этому тангенсу. В данном случае, угол будет примерно равен 26,565 градусам.

Таким образом, нахождение угла по известному тангенсу на калькуляторе — это простая и эффективная задача. Используя обратную функцию тангенса, можно легко определить значение угла, соответствующего заданному тангенсу.

Эта инструкция должна помочь вам в решении задач, связанных с вычислением угла по известному тангенсу на калькуляторе. Используйте ее для решения вашего случая и не стесняйтесь обращаться за помощью.

Определение квадранта для правильного значения угла

Когда мы говорим о вычислении угла с помощью его тангенса на калькуляторе, важно знать не только значение этого тангенса, но и в каком квадранте находится данный угол. Почему это так важно? Дело в том, что тригонометрические функции (в том числе тангенс) имеют разные значения в разных квадрантах.

Тригонометрический круг делится на четыре квадранта, обозначенных числами 1, 2, 3 и 4 соответственно. Каждый квадрант имеет свои характеристики, которые нам необходимо знать для правильного определения значения угла.

В первом квадранте (1) значение тангенса положительно, так как и значения синуса и косинуса. Это означает, что угол находится в диапазоне от 0 до 90 градусов. Например, если тангенс угла равен 1, то это может быть угол 45 градусов, так как тангенс 45 градусов также равен 1.

Во втором квадранте (2) значение тангенса отрицательно, а значения синуса и косинуса положительны. Это означает, что угол находится в диапазоне от 90 до 180 градусов. Например, если тангенс угла равен -1, это может быть угол 135 градусов, так как тангенс 135 градусов равен -1.

В третьем квадранте (3) значение тангенса положительно, но значения синуса и косинуса отрицательны. Это означает, что угол находится в диапазоне от 180 до 270 градусов. Например, если тангенс угла равен 1, это может быть угол 225 градусов, так как тангенс 225 градусов также равен 1.

В четвертом квадранте (4) значение тангенса отрицательно, а значения синуса и косинуса положительны. Это означает, что угол находится в диапазоне от 270 до 360 градусов. Например, если тангенс угла равен -1, это может быть угол 315 градусов, так как тангенс 315 градусов равен -1.

Итак, для правильного определения значения угла по его тангенсу, нужно учитывать квадрант, в котором находится данный угол. Это позволит нам представить углы в нужном диапазоне и избежать ошибок.

Практические примеры использования калькулятора для нахождения угла по тангенсу

В данной статье мы подробно рассмотрели, как использовать калькулятор для вычисления угла по его тангенсу. Но возможности калькулятора не ограничиваются только вычислением одного угла. Рассмотрим несколько практических примеров, в которых использование тангенса и калькулятора может быть очень полезным.

Пример 1: Расчет высоты объекта

Предположим, у вас есть длина тени, отбрасываемой объектом под углом 45 градусов, и вы хотите найти высоту этого объекта. Сначала найдите тангенс угла:

Тангенс угла = высота / длина тени

Зная длину тени и найдя тангенс угла с помощью калькулятора, вы сможете вычислить высоту объекта.

Пример 2: Определение расстояния между объектами

Предположим, вы находитесь на одной стороне реки и видите дерево, под которым на другом берегу находится дом. Вы хотите узнать, какое расстояние вам нужно преодолеть, чтобы добраться до дома. Для этого выполните следующие шаги:

1. Измерьте угол (например, с помощью компаса) между вашим положением и направлением на дерево.
2. Измерьте угол между деревом и домом (амплитуда).
3. Используйте тангенс угла между вашим положением и направлением на дерево, а также тангенс угла между деревом и домом, чтобы найти расстояние между вами и домом.

В этом случае, тангенс угла поможет вам найти расстояние между объектами с помощью калькулятора.

Пример 3: Навигация на яхте

При навигации на яхте или других судах, вам может понадобиться определить угол наклона яхты по отношению к нормальной поверхности во время плавания. Для этого можно использовать калькулятор и тангенс угла:

Тангенс угла = высота подводной части яхты / длина яхты

Зная тангенс угла, вы сможете определить угол наклона яхты и принять соответствующие меры для обеспечения безопасности и комфорта на борту.

Таким образом, возможности калькулятора и использование тангенса в вычислениях угла может быть полезным не только в учебных задачах, но и на практике в реальной жизни, в различных ситуациях, требующих точных расчетов и определения углов.