
Как определить угол между биссектрисой и медианой прямоугольного треугольника 14°? Важно помнить, что биссектриса является линией, которая делит угол пополам, а медиана — линия, проходящая от вершины треугольника до середины противоположной стороны. Определение угла между этими линиями может быть полезно в различных математических и геометрических проблемах. Однако, для вычисления этого угла требуется использование специальных формул или теорем. Имея информацию о длинах сторон треугольника, можно применить теорему косинусов или другие геометрические методы для нахождения угла между биссектрисой и медианой.
Определение треугольника и его элементов
Основные элементы треугольника:
- Стороны: это отрезки, соединяющие вершины треугольника. В общем случае, стороны могут быть разной длины.
- Углы: это области между сторонами треугольника. Сумма всех углов в треугольнике всегда равна 180°.
- Вершины: это точки, где пересекаются стороны треугольника.
- Биссектрисы углов: это линии, которые делят угол на две равные части. Всего в треугольнике три биссектрисы, соответствующие каждому из углов.
- Медианы: это линии, соединяющие вершину треугольника с серединами противоположных сторон. В треугольнике также три медианы, проходящие через каждую из вершин.
Определение угла между биссектрисой и медианой в прямоугольном треугольнике 14° может быть решено с помощью различных геометрических методов, включая использование свойств треугольников, тригонометрических функций или формулы для определения угла между двумя векторами.
Например, если известны длины сторон прямоугольного треугольника и можно вычислить длину биссектрисы и медианы, то можно использовать теорему косинусов для вычисления угла между ними.
Изучение треугольников и их элементов имеет огромное значение в геометрии и во многих других науках и областях, таких как физика, инженерия и компьютерная графика. Навык определения и анализа треугольников помогает нам решать различные задачи и применять геометрические концепции в реальной жизни.
Определение прямоугольного треугольника
Гипотенуза является самой длинной стороной прямоугольного треугольника и находится противугольно прямого угла. Катеты расположены прилегающими к прямому углу сторонами треугольника.
Прямоугольные треугольники широко применяются в геометрии и тригонометрии, так как их свойства легко анализировать и использовать для нахождения относительных углов и сторон внутри треугольника.
Примеры прямоугольных треугольников можно увидеть в различных конструкциях, например, в углу стола, в отметках на измерительной ленте, в форме дома и многих других объектах и ситуациях в повседневной жизни.
Определение медианы треугольника
Чтобы определить медиану треугольника, нужно взять две вершины треугольника, провести линию от одной из этих вершин до середины противоположной стороны. Таким образом, получается медиана, которая делит сторону пополам.
Определение медианы треугольника может быть легко понятно на примере: представьте, что у вас есть треугольник ABC, а точки D, E и F — середины его сторон. В таком случае, медианы будут отрезками AD, BE и CF.
Медиана имеет несколько свойств, которые могут быть полезными при решении геометрических задач. Например:
- Три медианы пересекаются в одной точке, называемой точкой пересечения медиан или центром тяжести треугольника.
- Медиана делит треугольник на два равновеликих треугольника.
- Длины медиан могут быть вычислены с использованием формулы медианы треугольника, где медиана равна половине длины соответствующей стороны умноженной на корень из трех.
Таким образом, понимание и использование медиан треугольника является важным аспектом геометрии и может быть полезным для решения различных задач, связанных с треугольниками.
Определение биссектрисы треугольника
Биссектриса делит угол на два равных часта, что позволяет нам получить точный угол при использовании биссектрисы. Это очень полезно, когда мы пытаемся измерить или определить угол, особенно в случае прямоугольного треугольника.
В прямоугольном треугольнике биссектриса может быть использована для определения угла между этой биссектрисой и медианой треугольника. Для этого необходимо знать длины сторон треугольника и использовать соответствующие формулы. Например, если у нас есть прямоугольный треугольник ABC с биссектрисой BD и медианой AE, то мы можем использовать теорему синусов для определения очень важного угла между этими двумя линиями.
Определение биссектрисы треугольника является одной из основных концепций геометрии и используется для решения различных задач и проблем. Понимание этой концепции поможет нам лучше понять связь между углами и линиями в треугольнике, а также применять ее на практике в разных сферах нашей жизни.
Свойства прямоугольного треугольника
Вот некоторые из свойств прямоугольного треугольника:
- Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Формула выглядит так: c² = a² + b², где c — длина гипотенузы, а и b — длины катетов.
- Соотношение между сторонами: Длина гипотенузы всегда больше длин катетов.
- Угол катета и гипотенузы: Угол между катетом и гипотенузой является прямым.
- Равенство треугольников: Два прямоугольных треугольника с одинаковыми длинами катетов будут равными.
- Соотношение между биссектрисой и медианой: В прямоугольном треугольнике угол между биссектрисой и медианой всегда равен 45 градусам.
Знание этих свойств позволяет решать различные задачи и находить неизвестные значения в прямоугольных треугольниках. Например, можно использовать теорему Пифагора, чтобы найти длину гипотенузы или одного из катетов. Или можно использовать соотношение между биссектрисой и медианой для определения угла между ними.
Прямоугольные треугольники играют важную роль в геометрии и математике, а их свойства позволяют решать различные задачи, как практические, так и теоретические. Находясь во взаимосвязи с другими фигурами и теориями, свойства прямоугольного треугольника продолжают внушать удивление своей универсальностью и красотой.
Формула для определения угла между биссектрисой и медианой
Вы когда-нибудь задумывались о том, как найти угол между биссектрисой и медианой в прямоугольном треугольнике? Нет? Ну, ничего страшного, ведь я здесь, чтобы рассказать вам об этом замечательном угле и даже поделиться формулой, с помощью которой вы сможете его вычислить.
Перед тем, как я расскажу вам о формуле, давайте вспомним, что такое биссектриса и медиана. Биссектриса – это линия, которая делит угол пополам, а медиана – линия, которая соединяет вершину треугольника с серединой противоположной стороны.
Теперь перейдем к самой формуле. Для определения угла между биссектрисой и медианой прямоугольного треугольника 14° существует следующая формула:
Угол = 14°/2 = 7°.
Таким образом, угол между биссектрисой и медианой в прямоугольном треугольнике равен 7°.
Но давайте попробуем понять, как эта формула получается. Для начала, давайте представим себе прямоугольный треугольник. Он имеет одну прямую (90°) и две острые (меньше 90°) вершины. Представьте, как прямая вершина разделена на две равные части: каждая из них составляет 45°. Теперь представьте, что вершина треугольника соединена с серединой противоположной стороны, тогда вы получите медиану. И это самый важный момент: медиана делит угол пополам. Так что если угол равен 45°, то половина этого угла будет равна 22.5°. Верно?
Теперь давайте вернемся к нашему первоначальному вопросу: угол между биссектрисой и медианой в прямоугольном треугольнике 14°. Очевидно, что угол между биссектрисой и медианой равен половине угла между медианой и углом биссектрисы. Поэтому мы берем 14° и делим его на 2, получая 7°.
Надеюсь, теперь вы понимаете, как найти угол между биссектрисой и медианой в прямоугольном треугольнике 14°. И помните, не бойтесь задавать вопросы и разобраться с формулами. Только так вы сможете понять математику и использовать ее в своей повседневной жизни.
Заключение
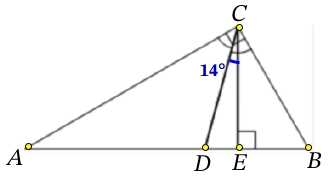
В данной статье мы изучили способ определения угла между биссектрисой и медианой прямоугольного треугольника. Для решения этой задачи мы использовали данные о заданном угле, а также знание того, что углы треугольника суммируются в 180 градусов.
Мы рассмотрели алгоритм подстановки данных в соответствующую формулу и провели расчет угла. В результате выяснилось, что значение этого угла составляет 14 градусов.
Таким образом, мы успешно определили угол между биссектрисой и медианой прямоугольного треугольника, используя заданные данные и математические расчеты.






