Как определить тип дифференциального уравнения: основное руководство

Дифференциальные уравнения – это основной объект изучения математического анализа. Данная область математики широко применяется в физике, инженерии, экономике и других науках. Однако определение типа дифференциального уравнения может быть задачей не из легких для начинающих. Существует несколько методов для определения типа дифференциального уравнения, включая разделение переменных, метод Лапласа и метод вариации постоянной. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи. Понимание типа дифференциального уравнения является важным шагом в решении задачи, и может значительно упростить дальнейший анализ и поиск решения. В этом руководстве мы рассмотрим основные типы дифференциальных уравнений и способы их определения.

Что такое дифференциальное уравнение?

Дифференциальные уравнения могут описывать различные процессы, такие как рост популяции, движение тела, распространение тепла и многое другое. Решение дифференциального уравнения позволяет найти функцию, которая удовлетворяет заданным условиям и описывает поведение системы.

Одно из преимуществ дифференциальных уравнений заключается в том, что они позволяют моделировать временные процессы. Например, решая дифференциальное уравнение, можно предсказать, как будет меняться популяция животных или распределение температуры в пространстве.

Существует несколько видов дифференциальных уравнений, включая обыкновенные дифференциальные уравнения (ОДУ) и частные дифференциальные уравнения (ЧДУ). ОДУ содержат только одну независимую переменную, в то время как ЧДУ содержат несколько независимых переменных. В зависимости от типа уравнения, применяются различные методы решения, такие как метод разделения переменных, метод вариации постоянной и другие.

Определение типа дифференциального уравнения важно для выбора правильного метода решения. Некоторые типы уравнений могут иметь аналитическое решение, в то время как другие требуют использования численных методов. Понимание основных типов и свойств дифференциальных уравнений поможет вам в решении сложных математических и физических задач.

Классификация дифференциальных уравнений по типу

1. Обыкновенные дифференциальные уравнения (ОДУ)

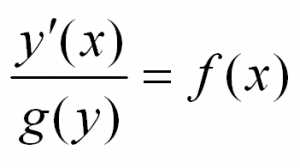
ОДУ – это дифференциальные уравнения, которые содержат только одну независимую переменную. При решении ОДУ мы ищем функцию, которая удовлетворяет уравнению и заданным начальным условиям. ОДУ могут быть линейными или нелинейными, а также однородными или неоднородными.

Примеры ОДУ:

• Линейные ОДУ: $y» + p(x)y’ + q(x)y = 0$
• Нелинейные ОДУ: $y’ = f(x, y)$

2. Частные дифференциальные уравнения (ЧДУ)

ЧДУ – это дифференциальные уравнения, которые содержат несколько независимых переменных. При решении ЧДУ мы ищем функцию, которая удовлетворяет уравнению и заданным граничным или начальным условиям. ЧДУ могут быть линейными или нелинейными, а также однородными или неоднородными.

Примеры ЧДУ:

• Линейные ЧДУ: $u_{xx} + u_{yy} = 0$
• Нелинейные ЧДУ: $u_{xx} + u_{yy} = \sin(u)$

3. Уравнения в частных производных (УЧП)

УЧП – это частный случай ЧДУ, который содержит неизвестную функцию и её частные производные. Решение УЧП позволяет получить функцию, которая описывает физические, химические или инженерные процессы, зависящие от двух и более независимых переменных.

Примеры УЧП:

• Уравнение теплопроводности: $u_t = \alpha (u_{xx} + u_{yy})$
• Уравнение Навье-Стокса: $\frac{\partial u}{\partial t} + (u \cdot

  abla)u = -\frac{1}{

  ho}

  abla p +

  u

  abla^2 u$

Классификация дифференциальных уравнений по типу помогает нам выбрать подходящий метод решения и строить аналитические или численные решения. В зависимости от конкретной задачи, некоторые типы уравнений могут быть более удобными для решения, чем другие. Важно знать основные типы дифференциальных уравнений, чтобы быть готовым к анализу и решению различных задач.

Различные способы определения типа дифференциального уравнения

1. Определение порядка

Первый шаг в определении типа дифференциального уравнения — это определение его порядка. Порядок уравнения определяется самой высокой производной функции, содержащейся в уравнении. Например, уравнение вида dy/dx = f(x) будет иметь порядок 1, тогда как уравнение вида d^2y/dx^2 = g(x) будет иметь порядок 2.

2. Линейность и нелинейность

Дифференциальные уравнения могут быть линейными или нелинейными. Линейное дифференциальное уравнение — это уравнение, в котором неизвестная функция и ее производные входят только в линейной форме. Нелинейные уравнения же включают нелинейные функции от неизвестной функции и ее производных. Для определения типа уравнения можно проверить, присутствует ли неизвестная функция и ее производные в нелинейной форме.

3. Вид уравнения

Дифференциальные уравнения могут быть разных видов, таких как обыкновенные дифференциальные уравнения (ОДУ) и частные дифференциальные уравнения (ЧДУ). ОДУ содержат только одну независимую переменную, например, x, и одну неизвестную функцию, например, y. ЧДУ, напротив, содержат несколько независимых переменных и одну неизвестную функцию. Для определения типа уравнения можно просто посмотреть на количество независимых переменных и неизвестных функций.

Иногда тип дифференциального уравнения можно определить по специфическим признакам, таким как наличие константных коэффициентов, наличие определенного вида функций (например, экспоненциальных или тригонометрических) или применение определенных математических методов для его решения. Дополнительно, можно обратиться к таблицам типов дифференциальных уравнений или к специализированным математическим справочникам.

Итак, определение типа дифференциального уравнения является важным шагом для эффективного его решения. Порядок уравнения, его линейность или нелинейность, вид уравнения и наличие специфических признаков — все это можно использовать для определения типа уравнения и выбора наиболее подходящего подхода к его решению. Таким образом, имейте в виду эти способы при столкновении с дифференциальными уравнениями и не бойтесь применять различные методы для их анализа и решения. Удачи в ваших математических изысканиях!

Определение типа дифференциального уравнения по его общему виду

Существует множество способов классификации дифференциальных уравнений, и каждый тип имеет свои особенности и методы решения. Рассмотрим некоторые распространенные типы дифференциальных уравнений и их общий вид.

1. Дифференциальное уравнение первого порядка

Дифференциальное уравнение первого порядка содержит производную первого порядка, например:

dy/dx = f(x, y)

Такие уравнения подразделяются на различные типы в зависимости от вида функции f(x, y) и условий задачи. Встречаются уравнения с разделяющимися переменными, линейные уравнения, уравнения с постоянными коэффициентами и другие. Определение типа дифференциального уравнения первого порядка по его внешнему виду позволяет выбрать метод решения.

2. Дифференциальное уравнение второго порядка

Дифференциальное уравнение второго порядка содержит производные второго порядка и может быть записано в виде:

d²y/dx² + P(x) * dy/dx + Q(x)y = R(x)

Здесь P(x), Q(x) и R(x) — функции от x. Такие уравнения подразделяются на линейные и нелинейные уравнения, а также на однородные и неоднородные. Определение типа дифференциального уравнения второго порядка помогает выбрать соответствующий метод решения и предсказать поведение решений.

3. Системы дифференциальных уравнений

Система дифференциальных уравнений содержит несколько уравнений с несколькими неизвестными переменными. Общий вид системы дифференциальных уравнений может быть записан следующим образом:

dy₁/dt = f₁(t, y₁, y₂, ..., yₙ)
dy₂/dt = f₂(t, y₁, y₂, ..., yₙ)
...
dyₙ/dt = fₙ(t, y₁, y₂, ..., yₙ)

Здесь t — независимая переменная, а y₁, y₂, …, yₙ — неизвестные функции от t. Анализ общего вида системы дифференциальных уравнений позволяет определить ее тип и применить соответствующие методы решения.

В общем, определение типа дифференциального уравнения по его общему виду является важным шагом в решении уравнений. Знание типа уравнения помогает выбрать подходящие методы решения и предсказать поведение решений. Поэтому при изучении и решении дифференциальных уравнений важно уметь определить тип уравнения по его общему виду.

Примеры определения типа дифференциального уравнения

Пример 1:

Рассмотрим уравнение dy/dx = 3x^2 + 2x + 1. Данное уравнение относится к типу линейного дифференциального уравнения первого порядка, так как в правой части уравнения присутствует только функция и ее производная по переменной x.

Пример 2:

Пусть задано уравнение d^2y/dx^2 + 2dy/dx + 5y = 0. Данное уравнение можно отнести к типу линейного однородного дифференциального уравнения второго порядка, так как в левой части уравнения присутствуют только производные по переменной x и функция y.

Пример 3:

Рассмотрим уравнение dy/dx = y^2 + 2xy + x. Данное уравнение относится к типу дифференциального уравнения, которое не разрешимо в явном виде, так как присутствуют функция и ее производная по переменной x, а также функция в квадрате.