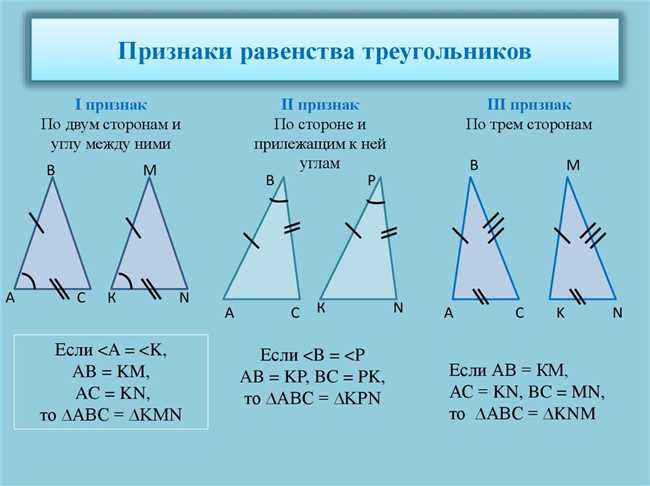
Равные треугольники — это треугольники, у которых все стороны и все углы равны. Для определения равенства двух треугольников важно учитывать несколько правил и методов.
Одним из основных правил является правило SSS (сторона-сторона-сторона), которое утверждает, что если все стороны одного треугольника равны соответствующим сторонам другого треугольника, то они равны. Например, если сторона AB первого треугольника равна стороне DE второго треугольника, сторона AC равна стороне DF и сторона BC равна стороне EF, то треугольники равны.
Другим методом определения равных треугольников является метод SAS (сторона-угол-сторона). Он утверждает, что если две стороны и угол между ними в одном треугольнике равны соответствующим сторонам и углу в другом треугольнике, то они равны. Например, если сторона AB первого треугольника равна стороне DE второго треугольника, угол A первого треугольника равен углу D второго треугольника и сторона BC первого треугольника равна стороне EF второго треугольника, то треугольники равны.
Правила и методы определения равных треугольников позволяют выявлять равенство треугольников и использовать его в решении различных геометрических задач.
Правило SSS для определения равных треугольников
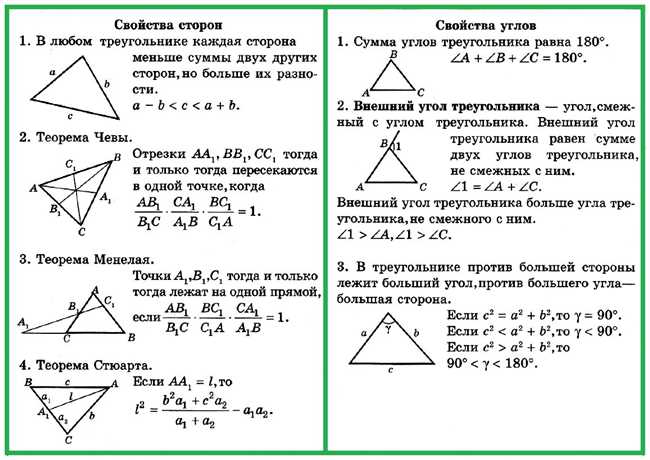
Теперь давайте посмотрим, как можно использовать правило SSS для решения задач на определение равных треугольников:
- Если в условии задачи даны значения длин всех трех сторон двух треугольников и они равны, то можно утверждать, что треугольники равны по правилу SSS.
- Если в условии задачи даны значения длин двух сторон одного треугольника и длина стороны другого треугольника и эти значения совпадают, то можно утверждать, что треугольники равны по правилу SSS.
Это лишь некоторые из возможных примеров. Ключевая идея здесь заключается в сравнении длин всех трех сторон двух треугольников. Если они совпадают соответственно, то треугольники считаются равными по правилу SSS.
Таким образом, правило SSS является мощным инструментом определения равных треугольников. Используя это правило, можно с легкостью определить, равны ли треугольники, и решить множество задач, связанных с треугольниками.
Правило SAS для определения равных треугольников
Применение правила SAS может показаться сложным на первый взгляд, но на самом деле оно довольно простое и логичное. Просто обратите внимание на соответствующие стороны и углы двух треугольников и убедитесь, что они равны. Если это так, то треугольники равны по правилу SAS.
Правило ASA для определения равных треугольников
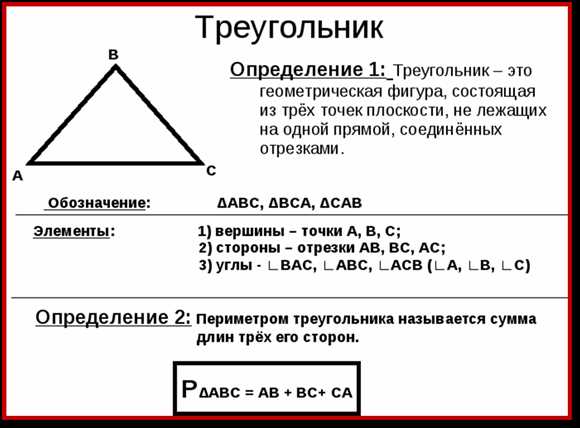
Давайте рассмотрим это правило на конкретном примере. Представьте, что у нас есть два треугольника — треугольник ABC и треугольник XYZ. Мы хотим определить, равны ли эти треугольники.
- Угол A треугольника ABC равен углу X треугольника XYZ.
- Сторона AB треугольника ABC равна стороне XY треугольника XYZ.
- Угол B треугольника ABC равен углу Y треугольника XYZ.
Согласно правилу ASA, такие треугольники равны. И это очень логично! Ведь если у нас есть два треугольника с одинаковыми углами и одинаковыми сторонами между этими углами, то они практически совпадают друг с другом.
ASA — это мощное правило, которое позволяет нам с уверенностью утверждать, что два треугольника равны. И помимо этого, оно помогает нам решать разнообразные геометрические задачи, которые требуют определения равенства треугольников.
Так что следуя правилу ASA, мы можем с уверенностью говорить о равенстве треугольников при наличии равных углов и сторон. Это правило предоставляет нам инструмент для более глубокого понимания и решения геометрических задач.
Правило AAS для определения равных треугольников
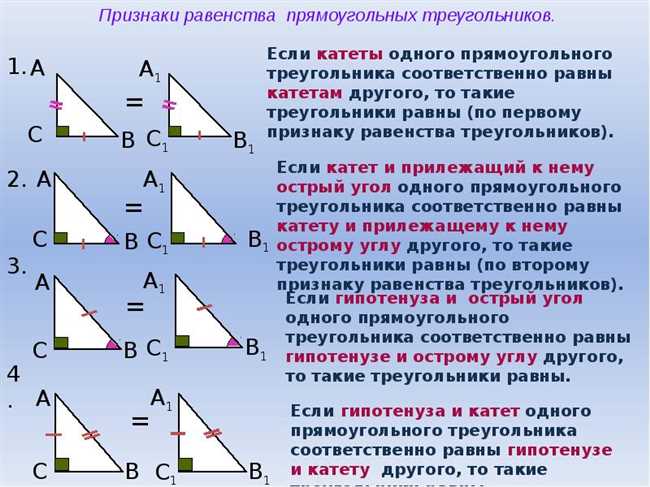
Применение правила AAS для определения равных треугольников требует выполнения следующих шагов:
- Сравниваем две стороны в первом треугольнике с двумя сторонами во втором треугольнике.
- Сравниваем угол между этими двумя сторонами в первом треугольнике с углом между соответствующими сторонами во втором треугольнике.
- Если стороны и угол совпадают, то треугольники равны.
Правило AAS является важным инструментом в геометрии, который позволяет определить равенство треугольников без необходимости измерять все стороны и углы. Это правило основано на концепции схожести фигур и может быть использовано для решения различных задач и примеров в геометрии.






