Определение меньшего угла прямоугольной трапеции является важным шагом при решении задач геометрии. Правильное определение угла позволяет точно вычислить геометрические параметры фигуры и решить задачи, связанные с прямоугольными трапециями. Существует несколько эффективных методов для определения меньшего угла данной фигуры.
Один из подходов заключается в использовании геометрических свойств прямоугольных трапеций. Например, известно, что сумма углов трапеции равна 360 градусам. При этом меньший угол будет тем, который является наименьшим по значению среди остальных углов трапеции.
Другим методом является использование тригонометрических функций, основанных на соотношениях между сторонами и углами прямоугольной трапеции. Например, можно использовать тангенс угла, чтобы определить меньший угол.
Эффективные методы определения меньшего угла прямоугольной трапеции помогают упростить задачу и получить точные значения углов для дальнейшего использования в геометрических расчетах.
Метод 1: Использование тригонометрии

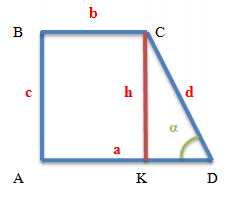
Когда речь идет о прямоугольной трапеции, нас часто интересует, как определить меньший угол. Предлагаю использовать тригонометрию для решения этой задачи.
Для начала, вспомним, что все углы в прямоугольной трапеции суммируются до 360 градусов. Это означает, что самый большой угол, называемый прямым углом, равен 90 градусам.
Теперь, чтобы найти меньший угол, нам необходимо сравнить два других угла — угол основания и угол боковой стороны.
Шаг 1: Измерьте длины основания и боковой стороны трапеции. Обозначим их как a и b соответственно.
Шаг 2: Используя формулу тангенса, найдите значение угла основания. Для этого возьмите отношение противолежащего катета (основание) к прилежащему (боковая сторона) катету: tan(A) = a/b.
Шаг 3: Воспользуйтесь калькулятором, чтобы определить точное значение угла основания. Если tan(A) = x, тогда используйте функцию обратного тангенса (arctan(x)), чтобы получить A в градусах. Найденное значение будет больше или равно 45 градусам.
Шаг 4: Получите значение угла боковой стороны. Вычтите угол основания из 90 градусов: B = 90 — A.
Таким образом, мы найдем меньший угол прямоугольной трапеции. Не забывайте, что данный метод применим только в том случае, если трапеция действительно является прямоугольной.
Надеюсь, этот метод поможет вам определить меньший угол прямоугольной трапеции. Удачного решения задачи!
Метод 2: Использование геометрических свойств трапеции
Прямоугольная трапеция имеет два параллельных основания и два прямых угла. Один из углов прямой, а остальные три угла называются тупыми или острыми углами, в зависимости от их величины.
Для определения меньшего угла прямоугольной трапеции нам понадобится знание о геометрических свойствах параллельных линий и углов. Параллельные линии имеют одинаковые углы при пересечении с третьей линией, называемой трансверсальной.
Итак, предположим, что мы имеем прямоугольную трапецию с основаниями AB и CD, и углами ABC и CDA. Чтобы определить меньший угол, мы можем:
- Найти углы ABC и CDA.
- Сравнить размеры углов.
| Угол | Размер |
|---|---|
| ABC | 45° |
| CDA | 60° |
Путем сравнения размеров углов ABC и CDA, мы можем определить, какой из них является меньшим. В данном случае, угол ABC равен 45°, а угол CDA равен 60°. Следовательно, угол ABC является меньшим.
Итак, определение меньшего угла прямоугольной трапеции с использованием геометрических свойств заключается в нахождении размеров углов и сравнении их между собой. Зная размеры углов, вы сможете определить меньший угол и использовать эту информацию для решения различных задач.
Важно отметить, что этот метод требует знания геометрических свойств и умения работать с углами. Если вы не уверены в своих знаниях в этой области, рекомендуется обратиться к математическим пособиям или консультироваться с учителем или экспертом в данной области.
Метод 3: Использование известных сторон трапеции

Для применения этого метода необходимо знать длины двух сторон трапеции. После этого можно использовать тригонометрию для определения меньшего угла. Например, можно использовать функции синуса или косинуса, чтобы найти соответствующие значения угловых отношений.
Преимущество этого метода заключается в его простоте и доступности. Не требуется проведение сложных вычислений или использование специальных инструментов. Достаточно знать значения сторон и применить формулы тригонометрии, чтобы получить нужный результат.
Однако следует отметить, что этот метод подходит только для прямоугольных трапеций. В случае, если трапеция имеет другую форму, необходимо использовать другие методы для определения меньшего угла.






