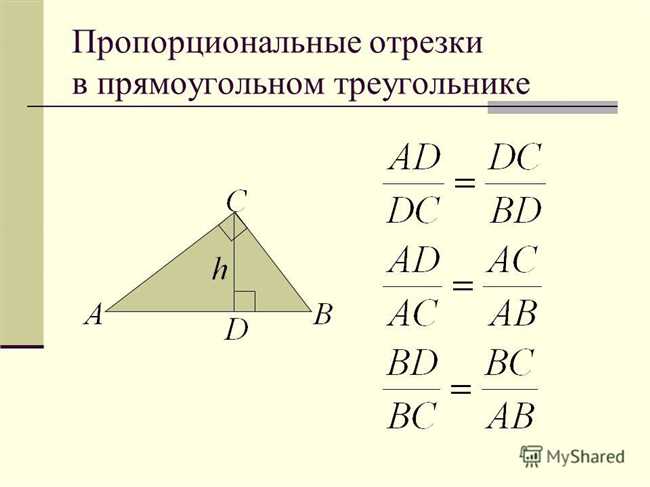
Определение и формула пропорциональных отрезков в прямоугольном треугольнике
В прямоугольном треугольнике можно найти пропорциональные отрезки, которые связаны с его гипотенузой и катетами. Пропорциональные отрезки имеют одно и то же отношение к другим отрезкам в треугольнике. Возьмем, к примеру, прямоугольный треугольник ABC, где AB — гипотенуза, BC — основание и AC — высота. Если провести прямую DE, параллельную гипотенузе, то отрезок DE будет пропорциональен отрезку BC и будет обозначаться как x. Соответственно, отрезок BE будет равен (1 — x). Формулу для нахождения пропорциональных отрезков можно записать как x = BC / AB. Таким образом, в прямоугольном треугольнике можно легко определить и вычислить пропорциональные отрезки с использованием указанных формул.
Понятие пропорциональных отрезков
Один из основных инструментов для работы с пропорциональными отрезками в прямоугольном треугольнике — это теорема Пифагора. Она гласит, что квадрат длины гипотенузы (самой большой стороны треугольника) равен сумме квадратов длин катетов (двух меньших сторон треугольника). Это можно записать формулой:
с² = а² + b²
Используя эту формулу, мы можем вычислить длину любого отрезка в прямоугольном треугольнике, если известны длины остальных отрезков.
Кроме того, в прямоугольном треугольнике существует понятие подобных треугольников. Два треугольника называются подобными, если соответствующие углы этих треугольников равны, а соответствующие стороны пропорциональны. Это означает, что отношения длин соответствующих сторон равны между собой.
Используя понятие подобных треугольников, мы можем также вычислить пропорциональные отрезки в прямоугольном треугольнике. Например, если мы знаем длину одного отрезка, то можем определить длины других отрезков, используя подобные треугольники и соотношение длин сторон.
Таким образом, понятие пропорциональных отрезков позволяет нам решать различные задачи, связанные с прямоугольными треугольниками. Оно является важным инструментом для геометрических расчетов и может быть использовано для различных практических целей.
Формула пропорциональных отрезков

Пропорциональные отрезки в прямоугольном треугольнике имеют особую формулу, которая выражает соотношение между длинами этих отрезков. Эта формула важна для нахождения неизвестных значений и использования их в различных задачах.
Формула пропорциональных отрезков в прямоугольном треугольнике основана на теореме Пифагора, которая устанавливает связь между длинами сторон треугольника. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов. Используя эту теорему, можно получить формулу для пропорциональных отрезков.
Формула выглядит следующим образом:
- Длина первого катета, умноженная на длину второго катета, равна произведению длины гипотенузы на длину сегмента гипотенузы, который является продолжением первого катета:
| Катет 1 | Катет 2 | Гипотенуза | Сегмент гипотенузы |
| a | b | c | d |
То есть, a * b = c * d.
Эта формула связывает длины отрезков, образованных в прямоугольном треугольнике, и позволяет находить пропорциональные значения. Путем подстановки известных значений в формулу можно вычислить неизвестные величины и использовать их в задачах.
Предлагаю тебе попробовать решить небольшую задачу, используя эту формулу:
Дан прямоугольный треугольник с катетами длиной 3 и 4. Найди длину гипотенузы и сегмента гипотенузы, который является продолжением первого катета.
Для решения данной задачи, нужно использовать формулу пропорциональных отрезков и подставить известные значения:
- Первый катет a = 3;
- Второй катет b = 4;
- Гипотенуза c — неизвестное значение;
- Сегмент гипотенузы d — неизвестное значение.
Теперь, подставляя значения в формулу, получаем:
3 * 4 = c * d
12 = c * d
Теперь можешь попробовать решить уравнение и найти значения гипотенузы и сегмента гипотенузы. Удачи!
Примеры использования формулы пропорциональных отрезков

Ниже представлены несколько примеров использования формулы пропорциональных отрезков:
-
Построение перпендикуляра к гипотенузе: Если известны пропорции, с которыми перпендикуляр делит гипотенузу, формула пропорциональных отрезков позволяет найти длину этого отрезка. Найденный отрезок будет перпендикуляром к гипотенузе.
-
Нахождение площади прямоугольного треугольника: Зная длины отрезков, которыми гипотенузу делит перпендикуляр, можно использовать формулу пропорциональных отрезков для нахождения площади треугольника. Площадь можно найти, умножив половину произведения отрезков на значение гипотенузы.
-
Вычисление неизвестных сторон треугольника: Если известна длина одной стороны прямоугольного треугольника и пропорции, с которыми гипотенуза делит эту сторону, формула пропорциональных отрезков позволяет находить длину остальных сторон.
Формула пропорциональных отрезков является мощным инструментом для решения геометрических задач и нахождения неизвестных значений в прямоугольных треугольниках. Ее использование позволяет упростить и ускорить процесс решения задач, а также найти точные значения отрезков и площадей. Умение применять эту формулу в различных практических ситуациях является важным навыком в области геометрии и математики в целом.






