Как определить длину математического маятника для достижения нужного периода колебаний в 1 секунду?

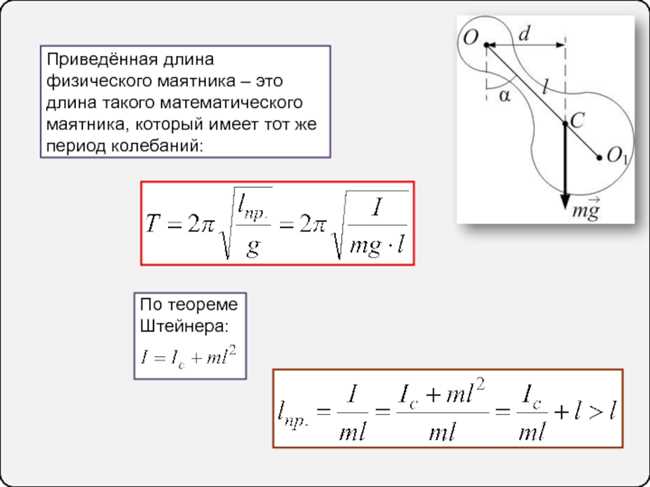
Длина математического маятника играет ключевую роль в определении его периода колебаний. Период колебаний — это время, которое требуется маятнику для совершения полного колебания, то есть для прохождения от одной крайней точки до другой и обратно. Для определения необходимой длины маятника, чтобы достичь желаемого периода колебаний, можно использовать формулу, основанную на законе сохранения энергии. Важно учитывать, что период колебаний также зависит от массы маятника и силы тяжести. Поэтому, чтобы получить точный результат, нужно учесть все эти факторы при определении длины математического маятника для нужного периода колебаний.

Длина математического маятника с периодом колебаний 1 секунда

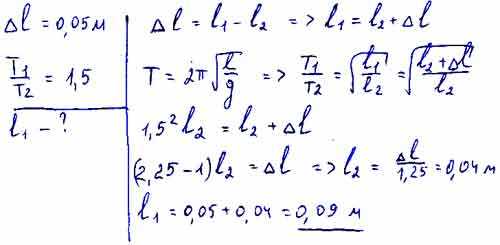
Вы когда-нибудь задумывались о длине математического маятника, который будет колебаться с периодом в одну секунду? Увлекательное задание, не так ли? Чтобы определить длину маятника для желаемого периода колебаний, нужно обратиться к формуле, которую Ньютон открыл еще в 1673 году.

Формула для расчета периода колебаний математического маятника выглядит следующим образом:

T = 2π√(L/g)

Где T — период колебаний, L — длина маятника, и g — ускорение свободного падения. В нашем случае, мы хотим получить период равный 1 секунде. Тогда:

1 = 2π√(L/g)

Для решения данного уравнения, нам необходимо знать ускорение свободного падения g. Величина ускорения свободного падения на Земле примерно равна 9,81 м/с². Используя эту информацию, мы можем решить уравнение и определить длину маятника:

L = (g * T²) / (4π²)

Подставим значения в данное уравнение, чтобы получить конкретную длину:

L = (9,81 * 1²) / (4π²) ≈ 0,248 метра

Таким образом, чтобы длина математического маятника обеспечивала период колебаний в одну секунду, необходимо, чтобы его длина составляла примерно 0,248 метра.

А что, если вы хотите найти длину маятника для периода колебаний не равного 1 секунде? Не проблема! Просто замените значение T в уравнении на ваш желаемый период, и решите уравнение снова. Вы удивитесь, какая длина маятника позволит ему колебаться с нужной вам частотой.

Определение понятия «математический маятник»

Математический маятник состоит из небольшого тела, называемого грузом, и нити, которая крепится к точке подвеса. Предполагается, что масса груза сосредоточена в одной точке и не распределена в пространстве.

Период колебаний математического маятника определяется его длиной и ускорением свободного падения. В идеальных условиях, без учета трения и воздушного сопротивления, период колебаний математического маятника равен 2π√(L/g), где L — длина нити, g — ускорение свободного падения. Таким образом, длина математического маятника можно определить, используя формулу:

L = (T^2 * g) / (4π^2)

Где L — длина нити, T — период колебания, g — ускорение свободного падения.

Для определения длины маятника с периодом колебаний 1 секунда, можно подставить значение периода T = 1 в формулу и решить ее относительно длины нити L:

L = (1^2 * g) / (4π^2)

Конечно, в реальных условиях существуют факторы, которые могут незначительно влиять на длину математического маятника, например, трение в подвесе или воздушное сопротивление. Однако, для большинства практических задач, эти влияния можно пренебречь и использовать формулу выше для определения длины маятника с нужным периодом колебаний.

В заключении, математический маятник — это простая и наглядная модель для изучения колебаний тела под действием силы тяжести. Определение его длины для нужного периода колебаний основано на простых физических законах и формулах, которые могут быть использованы для точного расчета.

Связь периода колебаний и длины математического маятника

Вы когда-нибудь задумывались о том, как определить длину математического маятника, чтобы получить нужный период колебаний? Эта проблема может быть актуальна при создании метронома, подвешенного к потолку или даже при строительстве маяка. Решение этого вопроса фактически основывается на связи, существующей между периодом колебаний и длиной маятника.

Период колебаний — это время, за которое маятник проходит полный цикл движения от максимального расстояния в одну сторону до максимального расстояния в другую сторону и обратно. Частота колебаний — это число колебаний, совершаемых маятником за определенный период времени. Длина маятника определяет его период колебаний и может быть рассчитана по формуле:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, π — математическая константа пи (приблизительно 3,14) и g — ускорение свободного падения (приблизительно 9,8 м/с²).

Итак, у нас есть формула, которая связывает период колебаний, длину маятника и ускорение свободного падения. Но как использовать эту формулу для определения длины маятника, при которой период колебаний будет равен 1 секунде?

Прежде всего, нам нужно решить эту формулу относительно длины маятника. Для этого мы возводим обе части уравнения в квадрат и делим на 4π²:

L = (T²g) / (4π²)

Теперь мы можем подставить значение периода колебаний, равное 1 секунде, и ускорение свободного падения, равное 9,8 м/с², в данную формулу для определения длины маятника:

L = (1² * 9,8) / (4 * 3,14²)

Выполнив простые вычисления, получаем:

L ≈ 9,87 метров

Таким образом, для того чтобы длина математического маятника обеспечивала период колебаний в 1 секунду, ее следует установить примерно равной 9,87 метра.

Итак, теперь, когда мы знаем, как определить длину математического маятника для нужного периода колебаний, мы можем использовать эту информацию в различных практических ситуациях. Например, при конструировании метронома или при строительстве маяка с механизмом с покачивающимся светом. Используя формулу и значения периода колебаний и ускорения свободного падения, мы сможем расчетно определить необходимую длину маятника и создать идеально работающее устройство.

Методы определения длины маятника для нужного периода колебаний

Задача определить длину математического маятника для достижения нужного периода колебаний может показаться сложной, но на самом деле существуют несколько методов, которые позволяют решить эту задачу. В этом тексте мы рассмотрим несколько из них.

Метод измерения колебаний

Один из наиболее простых и доступных методов – это измерение периода колебаний уже существующего маятника. Для этого можно использовать обычные секундомеры или специальные устройства, такие как фотоэлектрические датчики. Нужно просто запустить маятник и замерить время, за которое он совершает несколько колебаний. Зная время и количество колебаний, можно определить среднюю продолжительность одного колебания.

Для примера, предположим, что секундомер показывает 6 секунд для 10 колебаний. Это значит, что средняя продолжительность одного колебания равна 0.6 секунды. Если мы хотим достичь периода колебаний 1 секунда, то мы можем использовать эту информацию для определения длины маятника.

Метод математического вычисления

Для тех, кто предпочитает более точные и математические методы, есть также формула, которая позволяет определить длину маятника для нужного периода колебаний:

длина маятника = (период колебаний / (2 * π)) * (силы притяжения / коэффициента жесткости)

В этой формуле период колебаний измеряется в секундах, а сила притяжения и коэффициент жесткости – в Ньютонах и метрах соответственно.

Этот метод может быть более сложным для понимания и реализации, но он позволяет получить более точные результаты.

Метод использования таблицы или готового решения

Если вам не хочется проводить сложные вычисления или измерения, вы всегда можете воспользоваться таблицей или готовым решением для определения длины маятника. Научные и инженерные ресурсы часто содержат подобные таблицы и решения для различных типов маятников.

Например, вы можете найти таблицу, в которой указаны длины маятников с соответствующими периодами колебаний. Вам просто нужно найти значение близкое к нужному периоду и выбрать соответствующую длину маятника.

Также вы можете использовать готовое решение, которое приведет вас к нужному результату, основываясь на известных законах и формулах.

Используя один или несколько из этих методов, вы сможете определить длину математического маятника для нужного периода колебаний. Помните, что точность результата будет зависеть от точности ваших измерений и данных, на которые вы опираетесь.

Примеры решения задачи определения длины математического маятника

Существует несколько способов определения длины маятника для нужного периода колебаний. Ниже представлены два примера решения задачи:

Пример 1:

Чтобы определить длину маятника для нужного периода колебаний, можно использовать формулу для расчета периода:

T = 2π√(l/g)

где T — период колебаний, l — длина маятника, g — ускорение свободного падения (приближенно равно 9,8 м/с²).

Из данной формулы можно выразить длину маятника:

l = (T/2π)² * g

Подставив в данную формулу нужное значение периода колебаний T и ускорения свободного падения g, можно решить уравнение и найти длину маятника.

Пример 2:

Для определения длины маятника можно использовать формулу для расчета периода колебаний:

T = 2π√(l/g)

где T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Чтобы найти длину маятника, необходимо:

1. Задать значение периода колебаний T.
2. Подставить это значение в формулу и найти значение выражения √(l/g).
3. Возвести обе части уравнения в квадрат, чтобы избавиться от корня.
4. Разделить полученное уравнение на 4π², чтобы выразить длину маятника.
5. Подставить значение ускорения свободного падения g и решить уравнение для нахождения длины маятника.

Оба примера решения задачи определения длины маятника позволяют определить этот параметр на основе заданного периода колебаний. Выбор конкретного способа решения зависит от представленных величин и методов удобных для решения уравнений. Важно помнить, что точность решения может быть ограничена погрешностями измерений и использованными упрощениями модели математического маятника.