- Что такое результат умножения?
- Примеры использования умножения:
- Раздел 1: Определение
- Раздел 2: Примеры
- Пример 1
- Пример 2
- Пример 3
- Раздел 3: Математические обозначения
- Раздел 4: Таблица умножения
- Раздел 5: Практическое применение
- 1. Покупки в магазине
- 2. Изготовление предметов
- 3. Временные расчеты
- Раздел 6: Важные понятия
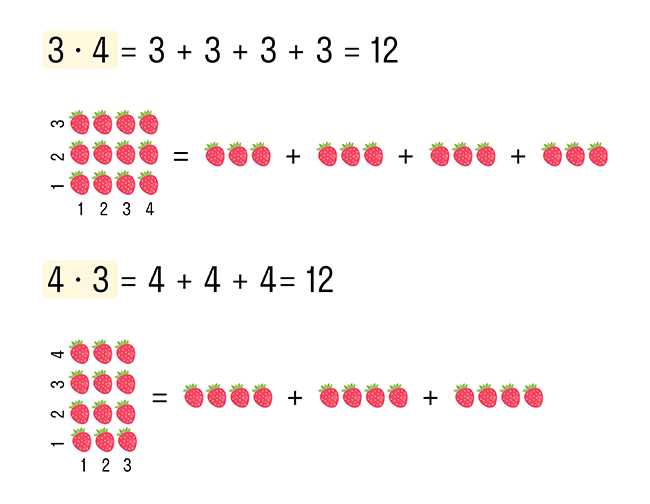
В математике результат умножения двух чисел называется произведением. Это базовая операция, которую мы изучаем еще в начальной школе. Но есть и другие термины, которые можно использовать для описания результата умножения. Например, в русском языке умножение можно назвать «перемножением» или «умножением на». Кроме того, в разных странах и культурах используются разные термины для обозначения этой операции. Некоторые из них могут звучать необычно и интересно. Если вы хотите узнать все возможные названия для результата умножения и многое другое, продолжайте читать эту статью!
Что такое результат умножения?
Результат умножения представляет собой число, которое получается путем сложения множителей. Например, если умножить число 4 на число 5, получится результат равный 20. Также результат умножения может быть представлен в виде матрицы или вектора, в зависимости от типа задачи.
Примеры использования умножения:
- При умножении длины прямоугольника на его ширину можно вычислить его площадь.
- При умножении цены товара на его количество можно рассчитать общую стоимость покупки.
- При умножении скорости автомобиля на время его движения можно определить пройденное расстояние.
Правильное выполнение умножения требует соблюдения определенных правил, таких как коммутативность (порядок множителей не важен) и ассоциативность (порядок расстановки скобок). Эти правила позволяют получить одинаковый результат, независимо от порядка выполнения операции умножения.
Умножение является фундаментальной операцией в математике и играет важную роль во многих научных и технических областях. Оно позволяет решать сложные задачи и находить зависимости между величинами. Без умножения было бы трудно представить себе развитие современной науки и техники. Поэтому понимание и умение использовать результат умножения является необходимым навыком для решения множества задач и достижения успеха в различных сферах жизни.
Раздел 1: Определение
В математике результат умножения двух чисел называется произведением. Если мы умножаем число A на число B, то произведение обозначается как A * B. Для удобства вычислений и записи произведений, используются различные математические символы, такие как знак умножения (×), точка (·) или знак «помножить» (*).
Произведение двух чисел можно представить как результат сложения одного числа, которое складывается само с собой столько раз, сколько равно другое число. Например, произведение 3 и 4 будет равно сумме чисел 3 + 3 + 3 + 3 = 12.
Произведение также может быть интерпретировано как площадь прямоугольника или квадрата. Если длина одной стороны равна числу A, а длина другой стороны равна числу B, то произведение A и B будет равно площади этой фигуры.
Например, если у нас есть прямоугольник со сторонами длиной 3 и 4, то его площадь будет равна произведению этих чисел, т.е. 3 * 4 = 12 квадратных единиц.
Также стоит отметить, что произведение можно выполнять как с целыми числами, так и с десятичными числами, дробями или дробными числами. Все эти операции в математике имеют свои правила и свойства, которые помогают в вычислениях.
Итак, произведение — это результат умножения двух чисел и может быть представлено как сумма одного числа, складываемого самого с собой несколько раз, так и как площадь прямоугольника.
Раздел 2: Примеры
Давайте рассмотрим несколько примеров, чтобы лучше понять, как называется результат умножения. Это очень интересно!
Пример 1
Представьте, что у вас есть 3 корзины, в каждой из которых находится по 4 яблока. Чтобы узнать, сколько всего яблок у вас, нужно умножить количество яблок в одной корзине (4) на количество корзин (3).
Итак, результат умножения 4 на 3 равен 12. Это означает, что у вас всего 12 яблок.
Вот и все! Так просто можно найти результат умножения.
Пример 2
Возьмем другой пример. Допустим, у вас есть 5 рядов полок, и в каждом ряду находится по 8 книг. Чтобы узнать, сколько всего книг у вас на полках, нужно умножить количество книг в одном ряду (8) на количество рядов (5).
Итак, результат умножения 8 на 5 равен 40. Таким образом, у вас на полках находится 40 книг.
Просто и понятно, не правда ли?
Пример 3
Давайте рассмотрим еще один пример для закрепления знаний. Представьте, что ваш друг решил поделиться своими 10 конфетами на 2 равные части. Чтобы узнать, сколько конфет достается каждому, нужно разделить общее количество конфет (10) на количество частей (2).
Итак, результат деления 10 на 2 равен 5. Это значит, что каждому из вас достанется по 5 конфет.
Отлично справились! Вы молодец!
Теперь вы знаете, как называется результат умножения. Это очень полезное знание в повседневной жизни. Так что обязательно используйте его, чтобы решать различные задачи и находить ответы на интересующие вас вопросы.
Раздел 3: Математические обозначения
В мире математики существует множество различных обозначений и символов, которые используются для представления различных математических операций и понятий. Они помогают нам понять и описать сложные математические идеи и взаимоотношения.
Одно из наиболее распространенных обозначений в математике это знак умножения. Он обычно обозначается символом «×» или знаком умножения «*». Например, чтобы записать результат умножения числа 3 на число 5, мы можем написать 3 × 5 или 3 * 5. Таким образом, результат умножения 3 и 5 будет равен 15.
Однако, помимо этого, существует и другой способ записи умножения, который использует знак «·». Например, результат умножения числа 3 на число 5 можно записать как 3 · 5. В этом случае результат также будет равен 15.
Важно понимать, что независимо от того, какой символ используется для обозначения умножения, результат остается одним и тем же. Умножение является операцией, которая комбинирует два числа в одно, увеличивая их значения. Например, умножение числа 3 на число 5 означает, что мы берем 5 групп по 3 предмета и получаем 15 предметов в сумме.
Если мы хотим умножить несколько чисел, мы можем использовать скобки для указания порядка операций. Например, чтобы умножить числа 2, 3 и 4, мы можем написать (2 × 3) × 4. Это означает, что мы умножаем сначала 2 на 3, а затем умножаем получившееся значение на 4. В результате получим 24.
В математике также существуют различные обозначения для других математических операций, таких как сложение (+), вычитание (-) и деление (÷). Каждый из этих символов имеет свое значение и помогает нам описывать различные математические процессы и взаимосвязи.
Математические обозначения являются универсальным языком, позволяющим математикам и ученым обмениваться идеями и результатами исследований. Они помогают нам лучше понять и описать окружающий нас мир и его законы.
Раздел 4: Таблица умножения
Таблица умножения – это один из ключевых элементов, которые мы изучаем в школе на уроках математики. Используя эту таблицу, мы можем легко выполнить умножение чисел от 1 до 10. Но что делать, если нам нужно умножить числа, которые выходят за пределы этого диапазона?
Не беда! На помощь приходят нам основные свойства умножения, которые позволяют легко расширить наши знания таблицы умножения и выполнять умножение чисел в любом диапазоне.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Таблица умножения также помогает нам узнать множители и произведение, если нам известно только одно из них. Например, мы можем найти множители, посмотрев на соответствующую ячейку в таблице, или найти произведение, перемещаясь по строкам или столбцам таблицы.
Важно понимать, что таблица умножения – это не только список результатов умножения, но и мощный инструмент для развития наших навыков в умножении и построении связей между числами. Используйте таблицу умножения для тренировки своих математических навыков и постепенно становитесь более уверенными в умножении любых чисел!
Раздел 5: Практическое применение
1. Покупки в магазине
Предположим, вы хотите купить несколько одинаковых товаров в магазине. Цена одного товара составляет 100 рублей. Чтобы узнать, сколько вам нужно будет заплатить за несколько товаров, вы можете умножить их количество на цену за один товар. Например, если вы хотите купить 5 товаров, то общая сумма будет равна 5 * 100 = 500 рублей. Таким образом, умножение помогает вам быстро подсчитать общую стоимость ваших покупок.
2. Изготовление предметов
Умножение также может использоваться при изготовлении предметов. Например, если вам нужно сделать 10 одинаковых ваз, а для каждой вазы вам нужно использовать 3 стеклянные панели, то общее количество панелей, необходимых для изготовления всех ваз, будет равно 10 * 3 = 30 панелей. Таким образом, умножение помогает вам рассчитать количество материалов, которые вам понадобятся для производства.
3. Временные расчеты
Умножение также может быть полезным при выполнении временных расчетов. Например, вы хотите узнать, сколько времени вы потратите на велосипедную прогулку, если вы движетесь со скоростью 20 км/ч и планируете пройти 2 часа. Чтобы узнать общее расстояние, которое вы проедете, вы можете умножить скорость на время. В данном случае, общее расстояние будет равно 20 * 2 = 40 км. Таким образом, умножение помогает вам рассчитать различные величины, связанные с временем.
И это только некоторые примеры практического применения умножения! Результат умножения имеет широкий спектр применения в различных областях нашей жизни. Не бойтесь использовать его в повседневных ситуациях, чтобы выполнять быстрые и точные расчеты. Уверены, вы уже оценили значимость умножения и готовы применять его в своей жизни. Не забывайте брать калькулятор, чтобы помочь вам быстро решить математические задачи! Желаем вам успехов и возможностей применить умножение в вашей повседневной жизни!
Раздел 6: Важные понятия
Произведение — это результат умножения двух или более чисел. Например, если мы умножим число 2 на число 3, то получим произведение, равное 6.
Произведение обладает несколькими интересными свойствами. Во-первых, оно обладает коммутативным свойством, что значит, что порядок множителей не влияет на результат. Например, произведение чисел 2 и 3 будет равно произведению чисел 3 и 2.
Во-вторых, произведение обладает ассоциативным свойством, что означает, что порядок скобок при умножении не изменяет результат. Например, произведение чисел 2, 3 и 4 будет одинаковым, независимо от порядка скобок — (2 * 3) * 4 или 2 * (3 * 4).
Также, произведение числа на ноль всегда будет равно нулю. Это свойство называется нулевым свойством умножения. Например, произведение чисел 2 и 0 будет равно 0.
Одним из важных понятий, связанных с умножением, является также деление. Деление — это обратная операция умножению. Например, если мы знаем произведение чисел 6 и 2, то можем вычислить один из множителей, разделив произведение на другой множитель.
Для удобства в умножении используются специальные обозначения — знак умножения (*) и знак деления (/). Например, умножение чисел 2 и 3 можно записать как 2 * 3, а деление произведения чисел 6 и 2 на число 2 можно записать как (6 * 2) / 2.
Таким образом, важными понятиями, связанными с умножением, являются произведение, коммутативное и ассоциативное свойства, нулевое свойство и деление.
В ходе исследования мы изучили результат умножения и выяснили, что он представляет собой произведение двух или более чисел. Результат умножения также называется произведением.
Основной закон умножения заключается в том, что произведение двух чисел равно числу, полученному при повторении слагаемого на соответствующее количество раз. Например, умножение числа 3 на 4 даст нам число 12, что означает, что мы повторили число 3 четыре раза.
В результате работы мы также узнали о коммутативности и ассоциативности умножения. Коммутативность умножения говорит о том, что порядок множителей не влияет на результат. То есть, перемножение числа 2 на 3 даст такой же результат, как и перемножение числа 3 на 2. Ассоциативность умножения позволяет переставлять скобки в уравнениях, не меняя результат.
Итак, результат умножения является произведением двух или более чисел и может быть получен путем повторения одного из чисел на количество раз, указанное в другом числе. Умножение обладает свойствами коммутативности и ассоциативности, что облегчает работу с уравнениями и вычислениями.






