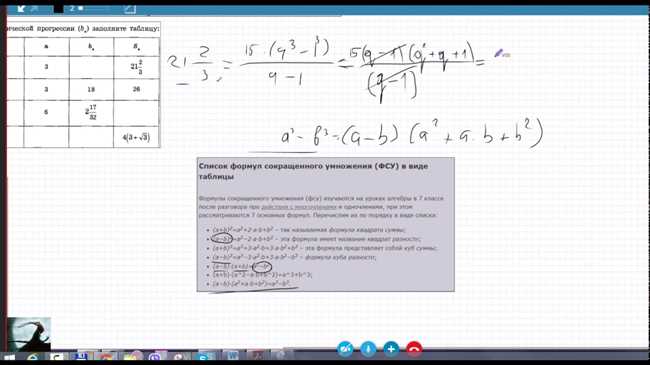
Как найти знаменатель геометрической прогрессии: подробный гайд
Прогрессия – это последовательность чисел, которая имеет определенный порядок. Геометрическая прогрессия является одним из типов прогрессий, где каждый следующий член получается умножением предыдущего на определенное число, называемое знаменателем. Нахождение знаменателя геометрической прогрессии – важный этап при решении математических задач. Для этого нужно знать как минимум два члена прогрессии. Существует несколько способов определения знаменателя геометрической прогрессии, включая формулу и использование соотношения. В данном статье мы рассмотрим подробный гайд по поиску знаменателя геометрической прогрессии с примерами и шагами к его определению.
Знаменатель геометрической прогрессии
Знаменатель геометрической прогрессии относится к числовой последовательности, где каждый следующий элемент получается умножением предыдущего элемента на одно и то же число, называемое знаменателем. Если мы хотим найти знаменатель геометрической прогрессии, у нас есть несколько способов.
Первый способ — это использование формулы для нахождения знаменателя геометрической прогрессии. Формула для нахождения знаменателя выглядит следующим образом:
an+1 = an * q
где an+1 — это следующий элемент геометрической прогрессии, an — предыдущий элемент геометрической прогрессии, а q — знаменатель геометрической прогрессии. Используя эту формулу, мы можем выразить знаменатель через предыдущий и следующий элементы:
q = an+1 / an
Таким образом, чтобы найти знаменатель геометрической прогрессии, необходимо разделить следующий элемент на предыдущий.
Если у нас нет информации о следующем элементе геометрической прогрессии, но у нас есть информация о нескольких элементах, мы можем использовать второй способ — использование отношения двух последовательных элементов.
Для этого необходимо выбрать два последовательных элемента геометрической прогрессии и поделить один на другой:
an+1 / an
Полученное отношение будет равно знаменателю геометрической прогрессии.
Знание знаменателя геометрической прогрессии может быть полезным при решении различных математических задач и применяется во многих областях, включая финансы, естественные науки и технику.
Определение и особенности геометрической прогрессии
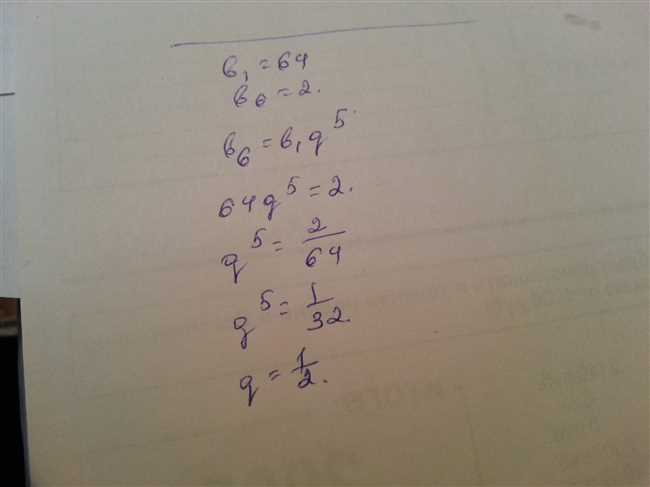
Простым способом представить себе геометрическую прогрессию, может быть последовательность чисел, в которой каждое следующее число больше предыдущего в одно и то же количество раз. Например, 2, 6, 18, 54 — здесь каждое следующее число больше предыдущего в 3 раза.
Определённая математическая зависимость, присущая геометрической прогрессии, отличает ее от других видов последовательностей чисел. В ГП, каждый элемент может быть вычислен, зная предыдущий элемент и знаменатель прогрессии. Например, чтобы найти пятый элемент ГП с первым элементом 2 и знаменателем 3, нужно умножить 2 на 3 (так как каждый последующий элемент получается умножением предыдущего на знаменатель). В результате получим пятый элемент равным 18.
Геометрическая прогрессия обладает несколькими особенностями:
- Каждый следующий элемент ГП может быть вычислен путем умножения предыдущего элемента на знаменатель;
- Значения ГП распределены экспоненциально, что означает, что разность между последовательными элементами увеличивается (или уменьшается) в геометрической прогрессии с положительным (или отрицательным) знаменателем;
- Знаковый знаменатель (положительный или отрицательный) определяет, будет ли каждое следующее число больше предыдущего или меньше его.
Геометрическая прогрессия широко используется в различных областях, включая математику, физику, экономику и даже в повседневной жизни. Знание основных свойств и способов работы с ГП может быть весьма полезным и помочь в решении различных задач и проблем.
Формула для нахождения знаменателя геометрической прогрессии
Как находить знаменатель геометрической прогрессии? Наверняка вы сталкивались с этим вопросом. Ну что ж, у меня есть ответ для вас! Формула для нахождения знаменателя геометрической прогрессии весьма проста и легко запоминается. Готовы узнать ее?
Перед тем, как мы перейдем к формуле, давайте вспомним, что такое геометрическая прогрессия. Она представляет собой последовательность чисел, где каждое следующее число получается умножением предыдущего числа на определенное число, называемое знаменателем прогрессии.
Теперь, когда мы освежили свою память, перейдем к формуле. Формула для нахождения знаменателя геометрической прогрессии выглядит следующим образом:
qn = a * r^(n-1)
где qn — n-ный член прогрессии, a — первый член прогрессии, r — знаменатель прогрессии, n — номер члена прогрессии, который мы хотим найти.
Эта формула основана на свойствах геометрической прогрессии. Знаменатель прогрессии — это число, на которое нужно умножать каждый предыдущий член прогрессии, чтобы получить следующий член. Поэтому, если у нас есть первый член прогрессии и номер члена, который мы хотим найти, мы можем использовать эту формулу для нахождения знаменателя.
Вот пример, чтобы лучше понять, как применять эту формулу. Представим, что у нас есть геометрическая прогрессия со знаменателем 2. Первый член этой прогрессии равен 1. Мы хотим найти четвертый член прогрессии. С помощью формулы, мы можем решить эту задачу следующим образом:
q4 = 1 * 2^(4-1) = 1 * 2^3 = 1 * 8 = 8
Таким образом, четвертый член прогрессии равен 8.
Надеюсь, теперь вам стало понятно, как использовать формулу для нахождения знаменателя геометрической прогрессии. Она может быть очень полезной в решении различных математических задач. Удачи вам!
Примеры расчета знаменателя геометрической прогрессии
Давайте рассмотрим несколько примеров расчета знаменателя геометрической прогрессии.
Пример 1:
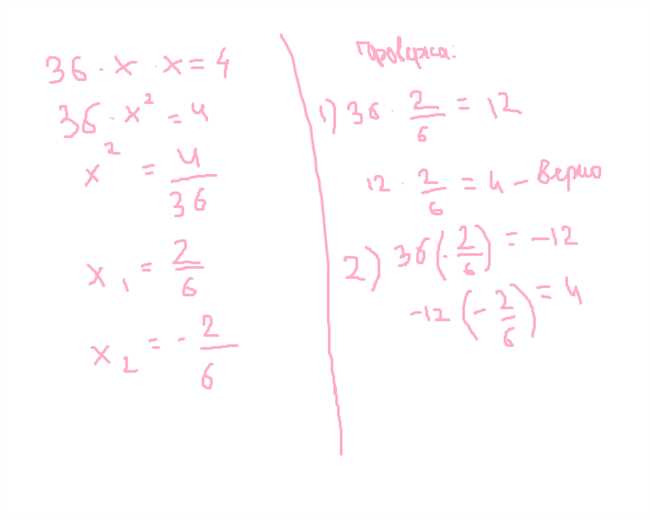
Пусть у нас есть геометрическая прогрессия с первым членом a = 3 и отношением r = 2.
Чтобы найти знаменатель прогрессии, мы используем формулу:
r = an+1 / an
где an+1 — следующий член прогрессии, а an — текущий член прогрессии.
Подставляя значения в формулу:
2 = an+1 / 3
Умножаем обе части уравнения на 3:
6 = an+1
Таким образом, знаменатель данной геометрической прогрессии равен 6.
Пример 2:
Рассмотрим следующую геометрическую прогрессию, где первый член a = 100 и отношение r = 0.5.
Используя ту же формулу, мы можем рассчитать знаменатель:
0.5 = an+1 / 100
Умножаем обе части уравнения на 100:
50 = an+1
Таким образом, знаменатель данной геометрической прогрессии равен 50.
Пример 3:
Давайте рассмотрим еще одну геометрическую прогрессию, где первый член a = 10 и отношение r = -3.
Проделываем те же шаги:
-3 = an+1 / 10
Умножаем обе части уравнения на 10:
-30 = an+1
Здесь знаменатель равен -30.
Итак, в каждом из этих примеров мы использовали формулу r = an+1 / an, заменили известные значения и решали уравнения, чтобы получить значение знаменателя геометрической прогрессии. Понимание и умение расчитывать знаменатель позволит вам эффективно работать с геометрическими прогрессиями и проводить различные математические операции.
Практическое значение знаменателя геометрической прогрессии
- Финансовая сфера: Знаменатель геометрической прогрессии используется для моделирования и прогнозирования процентных ставок, инфляции и других финансовых показателей. Он помогает банкам, инвесторам и экономистам принять обоснованные решения о вложении капитала и управлении рисками.
- Биология: В биологии знаменатель геометрической прогрессии используется для моделирования и исследования популяционной динамики, роста популяций и распространения заболеваний в популяции.
- Физика: В физике знаменатель геометрической прогрессии используется при описании радиоактивного распада вещества, затухания электрических сигналов и других процессов экспоненциального роста или убывания.
- Техника и информационные технологии: Знаменатель геометрической прогрессии находит применение при моделировании и оптимизации технических систем, а также в алгоритмах сжатия и передачи данных.
Понимание и использование знаменателя геометрической прогрессии помогает нам более глубоко анализировать различные процессы и явления в природе, науке и повседневной жизни. Благодаря этому понятию мы можем делать более точные прогнозы, принимать обоснованные решения и разрабатывать эффективные стратегии в различных областях деятельности.






