
Если вы занимаетесь математикой или изучаете анализ функций, то вам скорее всего понадобится найти значение производной функции в определенной точке. Поиск производной позволяет определить скорость изменения функции в данной точке. Знание этой информации может быть полезно при решении различных задач, таких как определение экстремумов или нахождение касательной к графику функции.
Для того чтобы найти значение производной функции fx в точке x0, необходимо применить определение производной и некоторые основные правила дифференцирования. Этот процесс может быть сложным и требует некоторых математических навыков. В данном руководстве мы подробно рассмотрим все необходимые шаги и дадим примеры, чтобы вам было легче разобраться в этой теме.
Вы готовы узнать, как найти значение производной функции в точке x0? Тогда давайте начнем!
Определение и свойства производной
Производная функции f(x) обозначается как f'(x) или dy/dx, где dy — это изменение значения функции, а dx — изменение значения аргумента. Определение производной включает предел и разность значений функции, и это определение можно записать следующим образом:
f'(x) = lim(h→0) (f(x+h) — f(x))/h
Где, f(x+h) — f(x) представляет собой разность значений функции, а h — приращение аргумента. Предел этой разности отношений при h→0 дает нам значение производной в точке x0.
Свойства производной функции обладают большим арифметическим и геометрическим значением. Некоторые из них:
- Правило суммы: Производная суммы двух функций равна сумме производных этих функций. То есть, если f(x) и g(x) — функции, то (f(x) + g(x))’ = f'(x) + g'(x).
- Правило произведения: Производная произведения двух функций равна произведению одной функции на производную второй и наоборот. То есть, если f(x) и g(x) — функции, то (f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x).
- Правило деления: Производная отношения двух функций можно найти с помощью формулы f(x) / g(x) = (f'(x) * g(x) — f(x) * g'(x)) / (g(x))^2.
- Правило композиции: Если функция f(x) является композицией двух функций g(x) и h(x), то производная этой композиции можно найти с помощью формулы f'(x) = g'(h(x)) * h'(x).
- Правило степенной функции: Производная функции вида f(x) = x^n, где n — целое число, равна n * x^(n-1).
Также производная функции может иметь различные физические интерпретации, такие как скорость изменения расстояния, скорость роста популяции или скорость изменения температуры. Знание производной позволяет нам анализировать и понимать различные процессы и явления в физике, экономике, биологии и других областях.
Методы нахождения производной
Существует несколько методов для нахождения производной функции. Рассмотрим некоторые из них.
1. Метод по определению
Метод по определению является одним из основных и простых способов нахождения производной функции. Он основан на пределе разности функции в точках, близких к данной.
Для нахождения производной функции f(x) в точке x0 с помощью метода по определению, необходимо выполнить следующие шаги:
- Найти значение функции f(x) в точке x0.
- Найти значение функции f(x) в некоторой другой точке x, близкой к x0.
- Найти разность между значениями функции f(x) в этих двух точках: f(x) — f(x0).
- Разделить полученную разность на разность между точками x и x0: (f(x) — f(x0))/(x — x0).
- Приближая точку x к x0, получим приближенное значение производной функции f(x) в точке x0.
Этот метод требует некоторых вычислений и приближений, но его применение основано на самом начале изучения производной функции.
2. Правила дифференцирования
В математике существуют некоторые основные правила дифференцирования, которые позволяют находить производную функции без применения метода по определению.
Вот некоторые из этих правил:
- Правило константы: Если функция f(x) = C, где C — константа, то ее производная равна нулю.
- Правило степенной функции: Если функция f(x) = x^n, где n — натуральное число, то ее производная равна nx^(n-1).
- Правило суммы: Если функция f(x) = g(x) + h(x), то ее производная равна сумме производных функций g(x) и h(x).
- Правило произведения: Если функция f(x) = g(x) * h(x), то ее производная равна произведению производной первой функции на вторую функцию и производной второй функции на первую функцию.
- Правило частного: Если функция f(x) = g(x) / h(x), то ее производная равна разности производной первой функции, умноженной на вторую функцию, и производной второй функции, умноженной на первую функцию, деленную на квадрат второй функции.
Применение правил дифференцирования значительно упрощает процесс нахождения производной функции, особенно при работе с более сложными функциями.
3. Независимое использование программного обеспечения

Помимо вышеперечисленных методов, также существует возможность использовать программное обеспечение для нахождения производной функции. Существуют коммерческие и бесплатные программы, которые позволяют точно определить значение производной функции в заданной точке.
Некоторые из таких программ включают в себя удобные и интуитивно понятные интерфейсы, что делает процесс нахождения производной еще более простым и понятным.
Заключение
Методы нахождения производной функции представлены различными способами, включая метод по определению, правила дифференцирования и использование программного обеспечения. Знание и применение этих методов позволяют более эффективно анализировать функции и их изменения.
Вычисление производной в конкретной точке
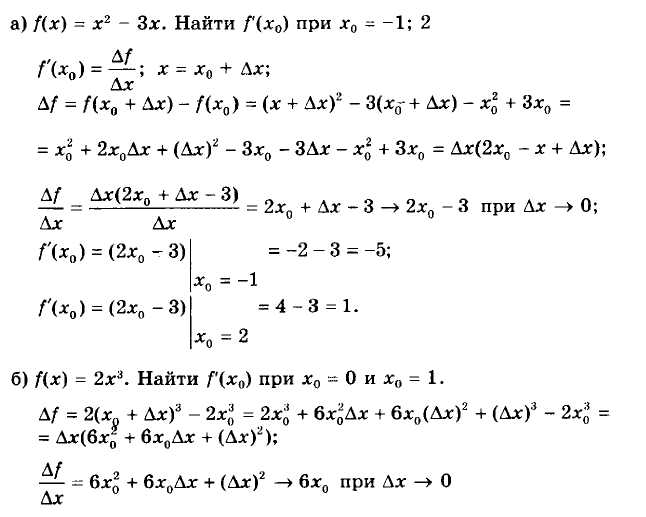
В данной статье мы рассмотрели важный вопрос: как найти значение производной функции в конкретной точке. Мы изучили различные методы и подходы к вычислению производной, которые позволяют нам найти точное значение производной в заданной точке.
Основной метод, который мы рассмотрели, это использование определения производной через предел. Этот метод позволяет нам точно вычислить значение производной в конкретной точке, но требует от нас некоторых математических навыков и времени на решение сложных уравнений.
Кроме определения производной через предел, мы также изучили другие методы: использование правила дифференцирования, приближенные методы и численные методы. Все эти методы позволяют нам найти приближенное значение производной в конкретной точке с различной степенью точности.
Вычисление производной в конкретной точке имеет большое значение в различных областях науки и применяется в различных задачах, таких как оптимизация, анализ данных, физика, экономика и многое другое. Правильное вычисление производной позволяет нам понять, как функция меняется в заданной точке и как эта информация может быть использована для решения практических задач.
- Мы рассмотрели различные методы расчета производной в конкретной точке;
- Определение производной через предел, правило дифференцирования, приближенные и численные методы;
- Вычисление производной имеет важное значение в научных и практических приложениях;
В заключении можно сказать, что вычисление производной в конкретной точке – это важная задача, которая помогает нам лучше понять поведение функций и использовать эту информацию для решения различных задач. На практике рекомендуется использовать несколько методов вычисления производной для получения более точных результатов и сравнения их между собой.






