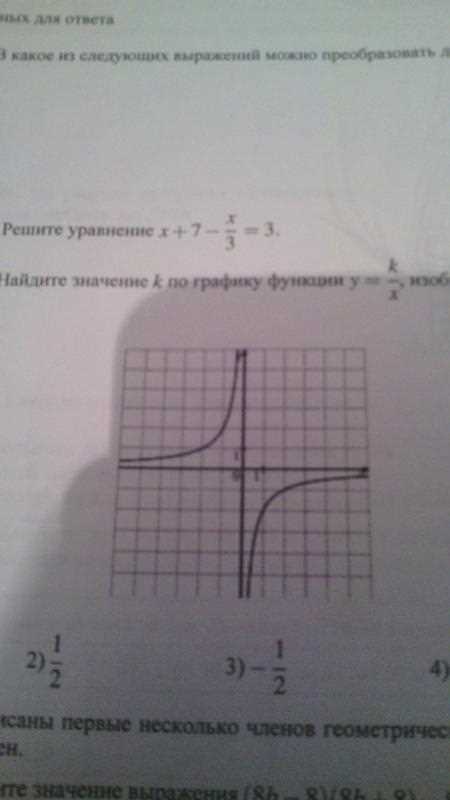
Когда мы работаем с графиками функций, нередко нам нужно найти значение некоторой переменной. Одним из распространенных случаев является поиск значения k. Для этого есть несколько шагов, которые могут помочь вам в решении этой задачи.
В первую очередь, нужно внимательно исследовать график функции. Определите экстремумы (максимумы и минимумы), точки перегиба и другие особенности графика. Затем, найдите точку на графике, где значение функции соответствует требуемому k.
Далее, определите координаты этой точки на графике и используйте их для нахождения значения k. Если график представлен в виде уравнения, подставьте координаты точки вместо переменных и решите уравнение для k.
Используйте эти шаги, чтобы найти значениe k по графику функции и успешно решить поставленную задачу.
Анализ графика функции
Когда мы анализируем график функции, мы можем обратить внимание на следующие аспекты:
- Пересечение с осями: Если функция пересекает ось абсцисс (ось X), то значение функции в этой точке будет равно нулю. Если функция пересекает ось ординат (ось Y), то мы можем определить значение функции в точке (0, k).
- Промежутки возрастания и убывания: Если функция строго возрастает на некотором интервале, то значение функции увеличивается с увеличением X. Если функция строго убывает, то значение функции уменьшается с увеличением X.
- Нули функции: Ноль функции — это значение X, при котором значение функции равно нулю. Нули функции можно найти, определив точки пересечения графика с осью абсцисс.
- Максимумы и минимумы: Максимум функции — это значение, наибольшее среди всех значений функции на определенном интервале. Минимум функции — это значение, наименьшее среди всех значений функции на интервале. Эти точки можно найти, определив точки перегиба или точки экстремума на графике функции.
Определение точек пересечения с осями координат
Определение точек пересечения с осями координат важно для анализа графиков функций и нахождения их значений. Когда график функции пересекает ось x, y или обе оси, это говорит о наличии определенных значений k, которые делают функцию равной нулю.
Для определения точек пересечения с осью x, мы должны найти значения x, при которых функция равна нулю. Для этого ставим уравнение функции равное нулю и решаем полученное уравнение относительно x. Найденные значения x являются точками пересечения с осью x.
Например, рассмотрим функцию f(x) = x^2 — 4x + 3. Чтобы найти точки пересечения с осью x, ставим функцию равной нулю и решаем уравнение:
x^2 — 4x + 3 = 0
Факторизуем это уравнение:
(x — 1)(x — 3) = 0
Получаем два возможных значения x: x = 1 и x = 3. То есть, функция пересекает ось x в точках (1, 0) и (3, 0).
Точки пересечения с осью y определяются подстановкой x = 0 в уравнение функции. Найденное значение y будет координатой точки пересечения с осью y.
В нашем примере функции f(x) = x^2 — 4x + 3, подставляя x = 0, получаем:
f(0) = 0^2 — 4 * 0 + 3 = 3
То есть, функция пересекает ось y в точке (0, 3).
Точки пересечения с обоими осями координат могут быть найдены, решив оба уравнения: уравнение функции равное нулю и уравнение для оси y (x = 0).
Итак, определение точек пересечения с осями координат важно для нахождения значений функции и анализа ее поведения. Путем решения уравнений, мы можем найти точки пересечения и легко определить значения k, при которых функция равна нулю. Это поможет нам лучше понять форму графика функции и использовать его для решения задач.
Нахождение точки максимума или минимума функции
Когда вы сталкиваетесь с задачей нахождения точки максимума или минимума функции, то это означает, что вам нужно найти точку, в которой функция достигает своего наибольшего или наименьшего значения на определенном интервале. Это очень важная задача, которую часто встречают в математике, анализе, физике и других науках.
Одним из способов нахождения точки максимума или минимума функции является аналитический метод. Этот метод основан на нахождении производной функции и поиске ее корней.
Производная функции показывает ее скорость изменения в каждой точке графика. Точки максимума или минимума находятся в тех местах, где производная равна нулю или не существует. Используя этот факт, можно написать уравнение для нахождения точки максимума или минимума функции.
Шаги аналитического метода:
- Найдите производную функции.
- Решите уравнение производной равной нулю или не существующей.
- Подставьте найденные значения в исходную функцию и определите значения k, которые соответствуют точкам максимума или минимума.
После выполнения этих шагов вы найдете значения k, при которых функция достигает своих экстремальных точек.
Но помимо аналитического метода, существует также графический метод нахождения точки максимума или минимума функции. В этом случае вам нужно построить график функции и визуально определить точку максимума или минимума. Для этого обратите внимание на форму графика, его выпуклость и изменение направления кривизны.
Оба метода являются эффективными и могут быть использованы в разных ситуациях. Аналитический метод требует более глубокого знания математических принципов, в то время как графический метод может быть более наглядным и понятным.
Использование экстремума для нахождения k
Пошаговая инструкция, описанная в данной статье, поможет вам найти значение параметра k по графику функции. Однако, в некоторых случаях можно воспользоваться методом использования экстремума для определения значения k.
Экстремум функции – это точка на графике, в которой функция достигает своего максимального или минимального значения. Для поиска значения k можно использовать экстремум функции при следующих условиях:
- Заданная функция имеет экстремум.
- График функции находится в той области, где экстремум функции определен.
Чтобы найти значение k с использованием экстремума, выполните следующие шаги:
- Обратите внимание на график функции и определите точку экстремума. Это может быть вершина параболы, точка перегиба или любая другая точка, где функция достигает максимального или минимального значения.
- Запишите координаты найденной точки экстремума.
- Подставьте координаты точки экстремума в уравнение функции и решите полученное уравнение относительно параметра k.
- Полученное значение k будет являться искомым значением.
Использование метода экстремума для нахождения значения параметра k может быть полезным в тех случаях, когда график функции имеет ярко выраженный экстремум и значения k могут быть связаны с его положением и формой.






