Как найти высоту ромба? Простые способы и формулы расчета

Как найти высоту ромба? Это вопрос, который может возникнуть при решении геометрических задач или при проектировании. Но не волнуйтесь, мы расскажем вам о простых способах и формулах расчета, которые помогут найти высоту ромба. Одним из эффективных методов является использование формулы, которая основана на площади ромба и длине одной из его сторон. Другой способ основывается на использовании теоремы Пифагора и длинах диагоналей ромба. Более подробно об обоих методах и их применении мы расскажем ниже.

Способы и формулы для расчета высоты ромба

Когда вам нужно найти высоту ромба, есть несколько простых способов и формул, которые могут помочь вам выполнить эту задачу. Рассмотрим некоторые из них.

1. Используйте формулу для высоты ромба на основе диагоналей

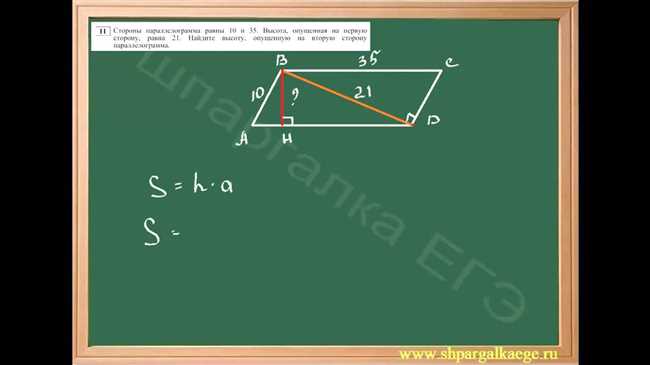
Если вам известны длины обеих диагоналей ромба, вы можете использовать следующую формулу для расчета его высоты:

h = sqrt(d1^2 — (a/2)^2) = sqrt(d2^2 — (a/2)^2)

Где h — высота ромба, d1 и d2 — длины диагоналей ромба, и a — длина одной стороны ромба. В этой формуле используется теорема Пифагора для нахождения высоты.

2. Используйте формулу для высоты ромба на основе одной стороны и угла

Если вам известна длина одной стороны ромба и величина одного из его углов, можно использовать следующую формулу для определения высоты:

h = a * sin(α)

Где h — высота ромба, a — длина одной стороны ромба, и α — величина угла в радианах. Эта формула основана на синусе угла между высотой и одной из сторон ромба.

3. Используйте формулу для высоты ромба на основе площади

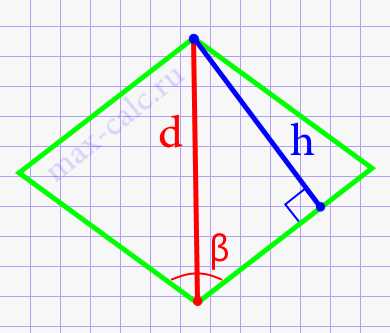
Если вам известна площадь ромба, можно воспользоваться следующей формулой для нахождения его высоты:

h = (2 * A) / a

Где h — высота ромба, A — площадь ромба, и a — длина одной стороны ромба. Эта формула основана на классической формуле для площади ромба (произведение диагоналей, деленное на 2).

Теперь вы знакомы с тремя простыми способами и формулами для расчета высоты ромба. Выберите тот, который наиболее удобен для вас и применяйте его с уверенностью!

Разделение ромба на два треугольника

Рассмотрим ромб со стороной a и высотой h, которая соединяет две противоположные вершины. Для нахождения высоты ромба, нам нужно разделить его на два треугольника, так чтобы каждый из них был прямоугольным. Понятно, что это будет треугольник, который получается после разделения диагоналями на две равные части.

Следуя этой идее, первый треугольник, который получится, будет иметь одну диагональ ромба и половину его стороны. Второй треугольник будет иметь вторую диагональ и ту же половину стороны. Оба треугольника получаются прямоугольными, так как мы разделили диагональ ромба на две равные части.

Теперь наша задача — найти высоту каждого из этих треугольников и сложить их, чтобы получить высоту ромба. Для этого нам потребуется использовать формулу для площади треугольника и высоты треугольника.

Формула для площади треугольника:

Площадь треугольника можно найти, умножив половину длины основания треугольника на его высоту:

S = (1/2) * a * h

Высота треугольника:

Высоту треугольника можно найти с помощью теоремы Пифагора, если известны длины сторон треугольника:

h = sqrt(c^2 — (a/2)^2)

Таким образом, для каждого из треугольников, имеющих одну из диагоналей и половину стороны ромба, мы можем найти их высоты, используя формулы выше, и затем сложить эти две высоты. Общая сумма высот треугольников будет равна высоте ромба.

Теперь, когда мы знаем, как разделить ромб на два треугольника и нашли формулы для высоты треугольника, вы можете легко найти высоту ромба, зная его сторону и применяя вышеуказанные формулы. Удачи!

Формула герона для расчета высоты

Формула Герона: высота = (2 * площадь) / (длина основы)

Чтобы применить данную формулу, необходимо знать не только стороны ромба, но и его площадь. Если вам известны только стороны, вам придется рассчитать площадь, используя другую формулу.

Возможно, у вас возник вопрос, а зачем знать площадь ромба, если нужно найти только его высоту? Ответ прост: площадь и высота ромба тесно связаны. Зная площадь, вы можете определить высоту с помощью формулы Герона.

После того, как вы рассчитали площадь ромба, просто подставьте значения в формулу Герона и найдите высоту. Эта формула особенно полезна, когда вы знаете длины всех сторон ромба, но не знаете его высоту.

Например, предположим, что у вас есть ромб с длинами сторон 6 см и 8 см, а его площадь равна 24 квадратных сантиметра. Чтобы найти высоту, используйте формулу Герона:

Высота = (2 * 24) / 6 = 8

Таким образом, высота ромба равна 8 сантиметрам.

Как видите, формула Герона дает нам простой и эффективный способ нахождения высоты ромба. Используйте ее при необходимости и с легкостью решайте задачи, связанные с геометрией!

Использование формулы смежных сторон и углов

Для начала, давайте вспомним некоторые особенности ромба. Ромб — это четырехугольник, все стороны которого равны между собой. Также все углы ромба равны между собой. Поэтому для вычисления высоты ромба мы можем использовать любую из его сторон и любой из его углов.

Для использования данной формулы нам понадобятся следующие параметры:

• сторона ромба (a)
• угол между этой стороной и высотой ромба (α)

Итак, формула для нахождения высоты ромба выглядит следующим образом:

h = a×sin(α)

Где:

• h — высота ромба
• a — длина одной из сторон ромба
• α — угол между этой стороной и высотой ромба

Для того чтобы воспользоваться этой формулой, нужно знать длину одной из сторон ромба и один из его углов.

Теперь давайте рассмотрим пример использования этой формулы:

Предположим, у нас есть ромб, у которого длина стороны равна 8 см. Нам также известно, что угол между этой стороной и высотой ромба равен 45 градусов. Мы хотим найти высоту этого ромба.

Используя нашу формулу, мы можем сделать следующие вычисления:

h = 8×sin(45)

sin(45) равен √2/2, поэтому:

h = 8×√2/2 = 8×0.707 = 5.656

Таким образом, высота ромба составляет 5.656 см.

Итак, мы использовали формулу смежных сторон и углов для нахождения высоты ромба. Эта формула оказывается очень полезной и простой в использовании. Теперь вы можете использовать ее в своих расчетах и вычислениях высоты ромба.

Применение теоремы Пифагора

Применение теоремы Пифагора особенно полезно в расчетах, связанных с нахождением высоты ромба. Высота ромба является перпендикуляром, проведенным из его вершины к противоположной стороне. Используя теорему Пифагора, мы можем найти длину высоты ромба, зная длины его сторон и диагоналей.

Для расчета высоты ромба по теореме Пифагора, необходимо знать длины двух его сторон и длины диагоналей. Для этогоприменяются следующие формулы:

• Для ромба со стороной a и диагоналями d1 и d2:
• Высота h = sqrt(d1^2 — (a/2)^2) или h = sqrt(d2^2 — (a/2)^2)

Таким образом, применение теоремы Пифагора позволяет нам легко расчитать высоту ромба, используя известные значения его сторон и диагоналей. Это особенно полезно в геометрии и строительстве, где знание высоты ромба может быть важным для правильного выполнения задачи.