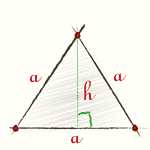
Высота равнобедренного треугольника — это отрезок, проведенный от вершины треугольника до основания, перпендикулярно основанию. Нахождение высоты треугольника может быть полезной задачей в геометрии и на практике. Однако, чтобы найти его, нужно следовать определенным шагам. Сначала, необходимо определить основание и боковые стороны треугольника. Затем, можно использовать теорему Пифагора, чтобы найти высоту, зная длину основания и боковую сторону. Другой способ — использовать формулу геометрического центра треугольника. Пошаговые инструкции помогут легко определить высоту равнобедренного треугольника и использовать это знание в повседневных ситуациях или в учебе.
Шаг 1: Понимание свойств равнобедренного треугольника
Может быть забавно выяснить, откуда берется название «равнобедренный». Во многих равнобедренных треугольниках линия, проходящая от вершины до основания, называется высотой. Если вы самолет или птица, вы летите по «высоте». Эта линия из центра земли приведет вас обратно вниз, на «основание».
Центр земли — это ваш угол, а линия по центру земли — это линия от основания к высоте.
Итак, когда мы говорим о высоте равнобедренного треугольника, мы обращаемся к линии, которая проходит от вершины этого треугольника до основания.
Теперь, когда у нас есть базовое представление о свойствах равнобедренного треугольника, мы можем двигаться далее и рассмотреть конкретные шаги для нахождения его высоты.
Шаг 2: Найти длины сторон треугольника
Теперь, когда мы знаем значение угла при основании треугольника, для нахождения его высоты нам понадобится вычислить длины его сторон. Высоту равнобедренного треугольника можно найти, используя теорему Пифагора.
Начнем с определения. Равнобедренный треугольник — это треугольник, у которого две стороны равны друг другу. Это означает, что мы можем обозначить длину каждой из равных сторон как «a», а длину третьей стороны как «c».
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае гипотенузой является сторона треугольника «c», а катетами — стороны «a».
Для нахождения длины сторон нам нужно воспользоваться теоремой Пифагора:
- Квадрат длины стороны «a» равен половине квадрата длины основания треугольника, так как треугольник равнобедренный. Это можно записать в виде a^2 = b^2 / 2, где «b» — длина основания треугольника.
- Длина стороны «c» равна квадратному корню из суммы квадратов длин сторон «a». То есть, c = √(a^2 + a^2), что равно c = √(2a^2).
Теперь мы знаем длины сторон треугольника. Остается только найти его высоту, приступим к этому в следующем шаге.
Шаг 3: Используйте теорему Пифагора для нахождения высоты
Мы можем записать это в виде уравнения: h^2 = a^2 — b^2, где h — высота треугольника, a — половина основания, и b — высота треугольника.
Используя известные значения длины основания и боковой стороны, мы можем подставить их в уравнение и решить его, чтобы найти значение высоты треугольника.
Пример:
- Предположим, что длина основания треугольника равна 10 см, а длина боковой стороны равна 8 см.
- Вычислим значение половины основания: a = 10 см / 2 = 5 см.
- Вычислим значение квадрата основания: a^2 = 5 см * 5 см = 25 см^2.
- Вычислим значение квадрата боковой стороны: b^2 = 8 см * 8 см = 64 см^2.
- Подставим значения в уравнение: h^2 = 25 см^2 — 64 см^2.
- Вычислим разность квадратов: h^2 = -39 см^2.
Как видно из примера, значение разности квадратов получается отрицательным. Это означает, что треугольник с такими характеристиками не существует. Высота не может быть вычислена в данном случае.
Однако, если вы получите положительное значение при решении уравнения, это будет длина высоты равнобедренного треугольника. Поздравляю! Вы успешно нашли высоту треугольника, используя теорему Пифагора.
Шаг 4: Воспользуйтесь формулой для нахождения площади треугольника
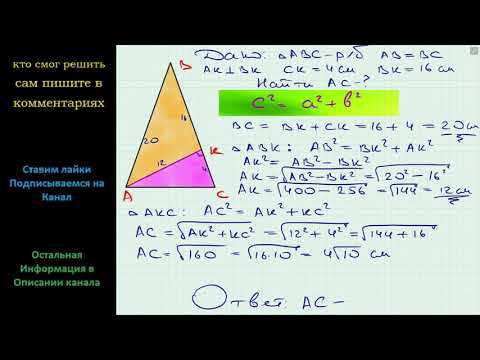
Теперь, когда мы знаем основание и высоту треугольника, мы можем использовать формулу для нахождения его площади. Формула звучит так:
Площадь треугольника = (основание × высота) ÷ 2
Давайте применим эту формулу к нашему равнобедренному треугольнику.
Предположим, что основание нашего треугольника равно 8 сантиметров, а высота — 5 сантиметров. Подставим эти значения в формулу:
Площадь треугольника = (8 см × 5 см) ÷ 2
Выполняем вычисления:
Площадь треугольника = 40 см² ÷ 2
Площадь треугольника = 20 см²
Таким образом, площадь нашего равнобедренного треугольника составляет 20 квадратных сантиметров.
Просто не могу не спросить – знаете ли вы, что такое основание и высота треугольника?
Шаг 5: Окончательно найдите высоту равнобедренного треугольника
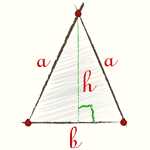
h = √(a^2 — (b^2 / 4))
Где:
- h — высота равнобедренного треугольника;
- a — длина стороны треугольника;
- b — длина основания треугольника.
Чтобы окончательно найти высоту равнобедренного треугольника, подставьте значения a и b в формулу и выполните необходимые математические операции. Округлите получившийся результат до нужной точности.
Теперь вы знаете, как найти высоту равнобедренного треугольника! При необходимости, вы можете использовать эту информацию для решения задач и выполнения вычислений с равнобедренными треугольниками.






