Как найти высоту параллелограмма по основанию и стороне: подробное объяснение и примеры

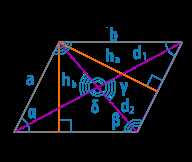
Когда вам даны только основание и одна из сторон параллелограмма, вы можете вычислить его высоту, используя определенную формулу. Для расчета высоты параллелограмма, вам нужно знать длину основания и длину относящейся стороны. Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны и равны. Его высота — это расстояние между этими параллельными сторонами, которое является перпендикуляром к основанию. Найдено точное математическое выражение для вычисления этой высоты, и она используется для нахождения вертикального расстояния между этими двумя параллельными сторонами параллелограмма.

Определение параллелограмма

Давайте подробнее рассмотрим особенности параллелограмма:

• Параллельные стороны: главной характеристикой параллелограмма является то, что его противоположные стороны параллельны. Это означает, что они не пересекаются и всегда равноудалены друг от друга.
• Равные стороны: параллелограмм также обладает свойством равных сторон, что означает, что его противоположные стороны имеют одинаковую длину.
• Равные углы: параллелограмм имеет две пары равных углов, то есть углы между параллельными сторонами имеют одинаковую меру.
• Смежные углы: все углы параллелограмма являются смежными, то есть они имеют общую сторону и не пересекаются.

Чтобы идентифицировать параллелограмм, достаточно проверить выполняются ли данные свойства: параллельность и равенство сторон, а также равные и смежные углы. Если все эти условия выполняются, то четырехугольник является параллелограммом.

Что такое параллелограмм?

Когда мы говорим о параллелограмме, первое, что приходит на ум, — это прямоугольник. И это верно! Прямоугольник — это особая разновидность параллелограмма, в которой все углы равны 90 градусов. Но параллелограммы могут иметь и другие формы и размеры. Важно помнить, что общее свойство всех параллелограммов — их параллельные стороны.

У параллелограмма есть несколько ключевых характеристик:

• Параллельные стороны: Все стороны параллелограмма параллельны и равны по длине.
• Равные противоположные углы: Противоположные углы параллелограмма равны между собой. Например, если один угол параллелограмма равен 60 градусов, то и противоположный угол также будет равен 60 градусов.
• Диагонали: Диагонали параллелограмма делят его на два треугольника. Диагонали параллелограмма имеют одинаковую длину и пересекаются в центре.

Теперь, когда мы знаем, что такое параллелограмм, давайте посмотрим, как можно найти его высоту, если известны основание и сторона.

Основные свойства параллелограмма

1. Параллельность сторон

Основное свойство параллелограмма — это параллельность противоположных сторон. Это означает, что если мы продолжим каждую сторону параллелограмма, они никогда не пересекутся. Параллельность сторон делает параллелограмм особенно удобным для измерений и вычислений.

2. Параллельность углов

В параллелограмме противоположные углы равны между собой. Если один угол параллелограмма равен, например, 60 градусов, то противоположный ему угол также будет равен 60 градусов. Это свойство может быть использовано для решения различных геометрических задач и для вычисления значений углов.

3. Равенство противоположных сторон

У параллелограмма противоположные стороны равны между собой. Это означает, что если одна сторона параллелограмма имеет длину 5 см, то ее противоположная сторона также будет иметь длину 5 см. Это свойство может быть использовано для проверки равенства сторон и для вычисления значений сторон.

4. Сумма углов параллелограмма

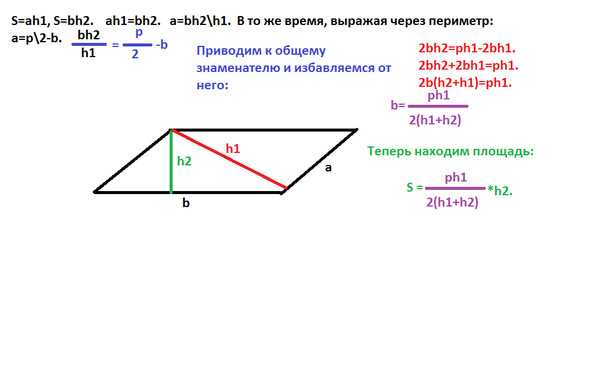
Сумма углов внутри параллелограмма всегда равна 360 градусам. Например, если у параллелограмма один угол равен 60 градусов, то сумма остальных трех углов будет равна 300 градусам. Это свойство может быть использовано для нахождения значений других углов параллелограмма.

5. Диагонали

Диагонали параллелограмма делят его на две равные части. Это значит, что если мы проведем диагональ от одного угла параллелограмма к противоположной стороне, она разделит параллелограмм на два равных треугольника. Это свойство может быть использовано для нахождения значений диагоналей и других сторон параллелограмма.

Это лишь несколько основных свойств параллелограмма, которые являются фундаментальными для понимания его структуры и применения в различных геометрических задачах. Изучив эти свойства и применяя их на практике, вы сможете легко работать с параллелограммами и решать задачи, связанные с этой фигурой.

Способы нахождения высоты параллелограмма

1. Использование формулы высоты

Первый способ – использование формулы для вычисления высоты параллелограмма. Формула выглядит следующим образом:

h = S / a

где h — высота параллелограмма, S — площадь параллелограмма, a — длина одного из его оснований.

Чтобы найти высоту параллелограмма с помощью этой формулы, необходимо знать площадь фигуры и длину одного из ее оснований. Такой подход может быть эффективным при решении математических задач или вычислении геометрических параметров конкретной параллелограмма.

2. Использование теоремы Пифагора

Второй способ нахождения высоты параллелограмма – использование теоремы Пифагора. Он основан на связи между сторонами и диагоналями параллелограмма. Для применения этого способа необходимо знать длины двух сторон и длину диагонали.

Для нахождения высоты параллелограмма по теореме Пифагора, необходимо воспользоваться следующей формулой:

h = √(b^2 — x^2)

где h — высота параллелограмма, b — одна из сторон параллелограмма, x — половина диагонали, перпендикулярной к данной стороне.

Этот способ может оказаться удобным, если вам известны не конкретные значения сторон и длины диагонали, а лишь их отношения или выражения через другие параметры. Также этот метод может помочь в определении максимальной высоты параллелограмма при заданных ограничениях.

3. Использование тригонометрических функций

Третий способ нахождения высоты параллелограмма – использование тригонометрических функций. Он основан на взаимосвязи между углами и сторонами параллелограмма. Для применения этого способа необходимо знать значения углов и сторон фигуры.

Формула для вычисления высоты параллелограмма с использованием тригонометрических функций выглядит следующим образом:

h = b * sin(α)

где h — высота параллелограмма, b — длина стороны, на которую опускается высота, α — угол между этой стороной и одним из оснований параллелограмма.

Этот способ может оказаться удобным, если вам известны значения углов и сторон параллелограмма, и вы хотите рассчитать высоту для конкретной комбинации параметров. Тригонометрия позволяет определить высоту фигуры на основе геометрических формул и угловых соотношений.

Высота параллелограмма является важной геометрической характеристикой, позволяющей более полно понимать и описывать эту фигуру. Нахождение высоты может быть полезно в учебе, строительстве, дизайне или других сферах деятельности, где требуется работа с геометрическими объектами. Используйте эти способы и углубляйте свои знания о параллелограммах!

Использование площади параллелограмма

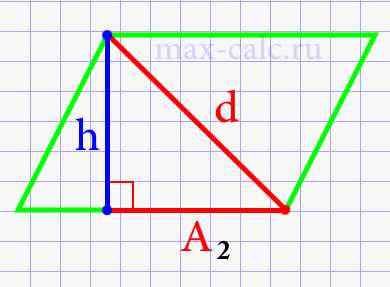
Вы уже знаете, как найти высоту параллелограмма, если известно его основание и одна из сторон. Как же это поможет вам в реальной жизни? Представьте, что вы работаете архитектором и вам нужно спроектировать крышу для здания, которая будет иметь форму параллелограмма. Для расчета необходимого количества материалов вам понадобится знать площадь параллелограмма.

Зная площадь, вы сможете определить, сколько материала понадобится для покрытия крыши. Это позволит вам не только оптимизировать расход материала, но и сэкономить деньги. Никто не хочет переплачивать лишнее за ненужные материалы, верно?

Кроме того, площадь параллелограмма может быть использована для оценки площади поля или сада. Если у вас есть карта участка с указанием длины основания и одной из сторон параллелограмма, вы сможете легко найти его площадь. Таким образом, вы сможете определить, какое количество земли вам потребуется приобрести для создания сада или посадки культурных растений.

Площадь параллелограмма может пригодиться и в будущих проектах или работах. Например, если вы решили отремонтировать пол в своем доме или офисе, вы можете использовать форму параллелограмма, чтобы правильно рассчитать количество необходимого вам напольного покрытия. Зная площадь комнаты, вы будете уверены, что закупаете достаточное количество материала.

В конце концов, знание площади параллелограмма может быть полезным в ежедневной жизни. Например, если вы занимаетесь дизайном интерьера, вы можете использовать параллелограммы для создания стильных мебельных композиций или световых сценариев.

Так что не думайте, что знания о параллелограммах и их площади не будут вам нужны. Они могут быть очень полезными, даже если вы не работаете в сфере строительства или дизайна. Знание этих математических концепций позволит вам лучше понимать пространственные отношения и применять их в повседневной жизни. Так что не бойтесь использовать площадь параллелограмма в своих проектах и задачах!

Использование формулы высоты параллелограмма

Если вам нужно найти высоту параллелограмма, и у вас есть информация об его основании и одной из сторон, то вы можете использовать следующую формулу:

Высота параллелограмма = (2 * площадь параллелограмма) / длина основания

Для начала вам необходимо найти площадь параллелограмма. Чтобы это сделать, умножьте длину основания на высоту параллелограмма. Если вам дана только одна сторона параллелограмма, вы можете использовать формулу площади треугольника: площадь треугольника = (0,5 * длина основания * высоту треугольника).

Когда вы найдете площадь параллелограмма, умножьте ее на 2 и разделите на длину основания, чтобы получить высоту параллелограмма. Эта формула основана на том факте, что высота параллелограмма является перпендикулярной основанию и проходит через его центр.

• Пример 1: Допустим, у вас есть параллелограмм со стороной 5 и основанием 8. Вы можете найти площадь параллелограмма: 5 * 8 = 40. Затем умножьте площадь на 2: 40 * 2 = 80. И наконец, разделите 80 на длину основания: 80 / 8 = 10. Высота параллелограмма равна 10.
• Пример 2: Предположим, у вас есть параллелограмм со стороной 6 и основанием 12. Найдите площадь параллелограмма: (0,5 * 6 * высоту треугольника). Например, высота треугольника может быть 8. Площадь треугольника будет (0,5 * 6 * = 24. Теперь умножьте площадь на 2: 24 * 2 = 48. И разделите 48 на длину основания: 48 / 12 = 4. Высота параллелограмма равна 4.

Используя эту формулу, вы сможете легко найти высоту параллелограмма, если у вас есть информация об его основании и одной из сторон. Помните, что при решении математических задач всегда стоит проверять свои вычисления и дважды убедиться в правильности ответа.

Заключение

В данной статье были рассмотрены примеры решения задач на нахождение высоты параллелограмма, при известных значениях основания и одной из сторон. Были использованы различные методы, позволяющие с легкостью найти нужное значение.

Одним из способов решения было использование теоремы о площадях треугольников, согласно которой площадь параллелограмма равна произведению длины основания на высоту. Используя это соотношение, можно легко найти высоту, зная площадь параллелограмма и длину основания.

Также был рассмотрен метод, основанный на применении теоремы Пифагора. Согласно этой теореме, квадрат длины высоты равен сумме квадратов длин основания и одной из сторон параллелограмма. Используя этот подход, можно быстро найти высоту, зная длины основания и одной из сторон.

Таким образом, при решении задач на нахождение высоты параллелограмма, можно использовать различные методы, описанные в данной статье. Важно понимать, что каждый метод имеет свои особенности и требует определенной информации. Однако, с помощью этих методов можно легко и точно найти высоту параллелограмма, что позволяет решать подобные задачи успешно.