Как найти высоту параллелепипеда: подробный гайд с примерами

Как найти высоту параллелепипеда: подробный гайд с примерами

В поисках высоты параллелепипеда? Не беспокойся, у меня есть для тебя подробный гайд с примерами! Независимо от того, нужна ли высота прямоугольного параллелепипеда, треугольного или неравномерного, этот гайд поможет тебе найти ответ. Как это работает? Просто загляни внутрь параллелепипеда и обрати внимание на одной из его граней. Измерь длину и ширину этой грани и запиши значения. Затем, измерь площадь этой грани и раздели ее на произведение длины и ширины. Полученное значение и будет высотой параллелепипеда! Подробные примеры помогут тебе лучше понять процесс и применить его на практике. Вот так просто находить высоту параллелепипеда! Теперь можешь приступать к своим измерениям.

Определение понятия «высота параллелепипеда»

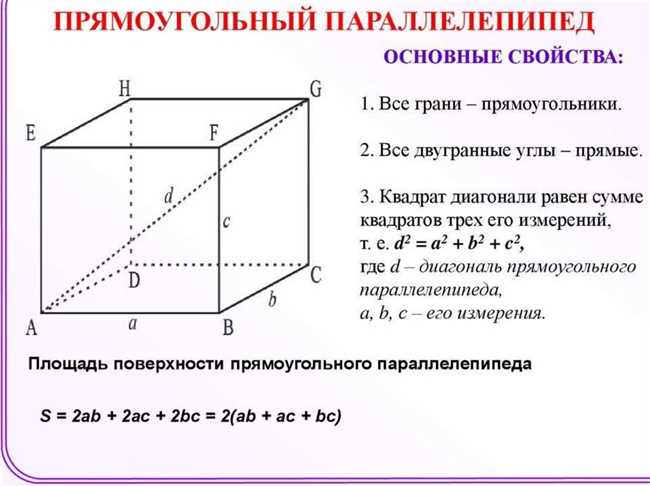
Параллелепипед — это трехмерная геометрическая фигура, имеющая шесть равных прямоугольных граней. Он отличается от куба тем, что его стороны могут иметь различные размеры.

Чтобы найти высоту параллелепипеда, необходимо знать длины его сторон. Обозначим эти стороны как a, b и c. Для нахождения высоты воспользуемся теоремой Пифагора для прямоугольного треугольника.

В прямоугольном треугольнике с катетами a и b и гипотенузой c, высота h соответствует одному из катетов и может быть найдена по формуле:

h = √(c^2 — a^2 — b^2)

Таким образом, для нахождения высоты параллелепипеда необходимо знать длины трех его сторон и подставить их в данную формулу.

Например, предположим, что длины сторон параллелепипеда равны a = 6 см, b = 8 см и c = 10 см. Подставим эти значения в формулу:

h = √(10^2 — 6^2 — 8^2) = √(100 — 36 — 64) = √(0) = 0

Таким образом, высота параллелепипеда в данном случае равна нулю, что означает, что параллелепипед является плоским, а не трехмерным объектом.

Высота параллелепипеда играет важную роль в геометрии и дает нам представление о его объеме и пространственной форме. Это понятие широко используется в различных областях, таких как архитектура, строительство, инженерия и графика.

Понятие параллелепипеда

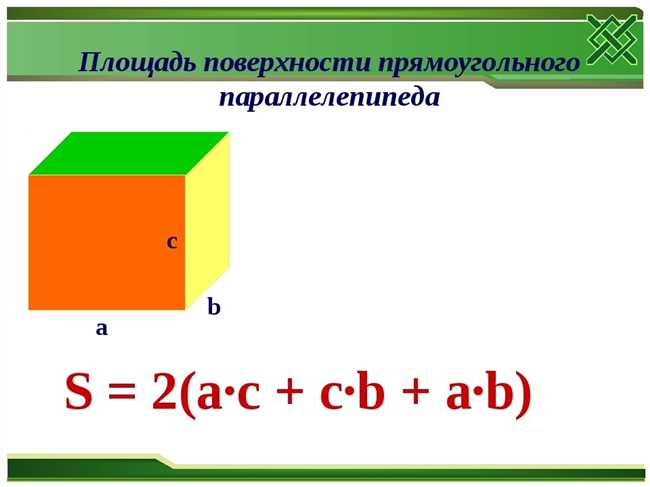
Параллелепипед – это пространственная геометрическая фигура, которая имеет шесть прямоугольных граней. Все его грани параллельны друг другу, что делает его особенным и уникальным. Интересно, что параллелепипед можно найти во многих повседневных предметах – от домашних книжных полок до строительных блоков.

Основные характеристики параллелепипеда – это его высота, ширина и длина. Высота – это расстояние между противоположными гранями, которое определяет, насколько фигура расположена в вертикальной плоскости. Ширина и длина – это соответственно расстояния между противоположными гранями в горизонтальной плоскости.

Теперь, когда у нас есть понимание о параллелепипеде, давай посмотрим на некоторые примеры, чтобы убедиться в его разнообразии и практической значимости.

• Возьмем, к примеру, ящик. Ящик – это прекрасный пример параллелепипеда, который мы нередко видим в нашей повседневной жизни. Он имеет шесть прямоугольных граней, позволяющих нам хранить в нем различные предметы.
• Построение – большая часть инженерной и строительной работы основана на использовании параллелепипедов. Блоки, кирпичи, стены и даже здания – все они имеют форму параллелепипеда и являются примерами этой удивительной геометрической фигуры.
• Аквариум – это еще один пример параллелепипеда, который может стать центром внимания в твоей комнате. Аквариумы имеют прямоугольную форму и позволяют нам наблюдать за живыми существами, обитающими в водной среде.

Теперь, когда мы разобрались с понятием параллелепипеда и рассмотрели несколько примеров, давай зададимся вопросом: почему это важно для нас? Ответ прост – знание геометрических фигур, таких как параллелепипед, поможет нам лучше понять и взаимодействовать с миром вокруг нас.

Любопытно, что параллелепипеды используются не только в повседневной жизни, но и в различных научных и инженерных областях. Они помогают в создании строительных проектов, проектировании и изготовлении мебели, а также в многих других сферах, связанных с пространственным мышлением.

Надеюсь, уважаемый читатель, что теперь ты хорошо представляешь себе, что такое параллелепипед и зачем он нам нужен. Продолжай интересоваться миром геометрии и находить новые примеры этой удивительной фигуры вокруг себя!

Определение высоты параллелепипеда

Когда мы говорим о параллелепипеде, мы нередко сталкиваемся с вопросом о его высоте. Но что такое высота параллелепипеда и как ее определить?

Высота параллелепипеда — это расстояние между двумя его параллельными плоскостями, которые перпендикулярны его основаниям. Определить высоту можно, зная длину одного из ребер параллелепипеда и площадь одного из его оснований.

Давайте рассмотрим пример. Предположим, у нас есть параллелепипед с длиной одного ребра равной 5 сантиметров и площадью основания равной 20 квадратных сантиметров. Как найти его высоту?

1. Найдем длину боковой грани параллелепипеда. Так как площадь одного из оснований равна 20 квадратным сантиметрам, то сторона этого основания равна квадратному корню из 20. Чтобы найти длину боковой грани, умножим длину стороны основания на корень из 2 (так как диагональ боковой грани параллелепипеда равна длине стороны основания умноженной на корень из 2):

Длина боковой грани = длина стороны основания * √2

Длина боковой грани = 5 * √2

2. Зная длину боковой грани параллелепипеда, можем определить его высоту. Высота параллелепипеда равна отношению площади одного из оснований к длине боковой грани:

Высота = площадь основания / длина боковой грани

Высота = 20 / (5 * √2)

3. Теперь можем рассчитать числовое значение высоты:

Высота = 20 / (5 * √2)

После выполнения всех вычислений получим значение высоты параллелепипеда. Таким образом, высота параллелепипеда в данном примере будет равна определенному числу.

Теперь вы знаете, как определить высоту параллелепипеда, используя длину одного из его ребер и площадь одного из его оснований. Это может быть полезным при решении различных геометрических задач или при простом измерении физических объектов вокруг нас.

Методы нахождения высоты параллелепипеда

Метод №1: Использование формулы

Первым и наиболее простым методом является использование формулы. Высоту параллелепипеда можно найти, зная площадь одной из его граней и длину одной из его сторон. Формула для вычисления высоты выглядит следующим образом:

h = S/A

где h — высота, S — площадь грани, A — длина стороны.

Пример: У нас есть параллелепипед с площадью грани S = 24 и длиной стороны A = 6. Найдем высоту:

h = 24/6 = 4

Таким образом, высота параллелепипеда равна 4.

Метод №2: Использование теоремы Пифагора

Если известны длины трех ребер параллелепипеда, то можно использовать теорему Пифагора для нахождения высоты. Этот метод подходит, когда измерения производятся со соседними ребрами параллелепипеда.

Для прямоугольного параллелепипеда теорема Пифагора имеет вид:

h = √(a^2 + b^2 — d^2)

где h — высота, a и b — длины ребер параллелепипеда, d — разность длин этих ребер.

Пример: У нас есть прямоугольный параллелепипед с a = 3, b = 4 и d = 1. Найдем высоту:

h = √(3^2 + 4^2 — 1^2) = √(9 + 16 — 1) = √24 = 4.9

Таким образом, высота параллелепипеда примерно равна 4.9.

Метод №3: Использование теоремы о трех перпендикулярах

Если известны высота, ширина и длина параллелепипеда, то можно воспользоваться теоремой о трех перпендикулярах для нахождения его высоты. Этот метод основан на свойствах перпендикуляров и позволяет найти высоту, даже если измерения производятся внутри параллелепипеда.

Формула для вычисления высоты выглядит следующим образом:

h = √(l^2 — (w/2)^2)

где h — высота, l — длина параллелепипеда, w — ширина параллелепипеда.

Пример: У нас есть параллелепипед с l = 5 и w = 3. Найдем высоту:

h = √(5^2 — (3/2)^2) = √(25 — 2.25) = √22.75 = 4.8

Таким образом, высота параллелепипеда примерно равна 4.8.

Итак, теперь вы знакомы с тремя методами нахождения высоты параллелепипеда. Каждый из них имеет свои преимущества и может быть применим в разных ситуациях. Попробуйте использовать эти методы при следующем измерении или расчете параллелепипеда, и вы обязательно получите желаемый результат!

Пример использования теоремы Пифагора

Давайте рассмотрим пример использования этой теоремы. Представьте, что у вас есть прямоугольный треугольник, стороны которого имеют следующие длины:

• Катет a: 3 см
• Катет b: 4 см

Теперь, применяя теорему Пифагора, мы можем вычислить длину гипотенузы треугольника. Возведем каждый из катетов в квадрат и просуммируем полученные значения:

a^2 + b^2 = 3^2 + 4^2 = 9 + 16 = 25

По теореме Пифагора, гипотенуза равна квадратному корню из полученной суммы. Применим эту формулу:

гипотенуза = √25 = 5 см

Таким образом, мы нашли длину гипотенузы треугольника, которая составляет 5 см. Теперь, зная длину гипотенузы, мы можем использовать эту информацию, чтобы решать более сложные задачи, такие как вычисление высоты параллелепипеда.

Пример использования теоремы Пифагора позволяет нам лучше понять, как применять эту теорему на практике. Она является важным инструментом в геометрии и имеет множество применений в различных областях, включая строительство, архитектуру и физику.

Пример использования метода проекций

Предположим, что у нас есть параллелепипед с длиной a = 5 м, шириной b = 3 м и высотой h, о которой мы хотим узнать. Мы можем использовать метод проекций для нахождения этой высоты.

Сначала давайте представим параллелепипед в виде плоской фигуры, которую мы можем проецировать на плоскость. В данном случае, мы можем проецировать параллелепипед на плоскость, параллельную одной из его сторон.

Представим, что мы выбираем плоскость, параллельную стороне a. Тогда мы можем увидеть проекцию параллелепипеда на эту плоскость как прямоугольник со сторонами b и h. Теперь мы можем использовать геометрические свойства прямоугольника для нахождения значения высоты h.

Длина прямоугольника b равна 3 м, поскольку это ширина нашего параллелепипеда. Мы знаем, что площадь прямоугольника равна произведению его длины на ширину. В данном случае, площадь прямоугольника равна a*b = 5 м * 3 м = 15 м².

Теперь мы можем использовать формулу площади прямоугольника для нахождения высоты h. Площадь прямоугольника равна длине стороны, параллельной проекции, умноженной на высоту.

15 м² = 3 м * h

Теперь мы можем решить это уравнение для высоты h, деля обе стороны на 3 м:

h = 15 м² / 3 м = 5 м

Таким образом, высота нашего параллелепипеда равна 5 м.

Метод проекций — это удобный и эффективный способ нахождения высоты параллелепипеда. Он позволяет использовать геометрические свойства плоских фигур для решения задач. Теперь вы можете использовать этот метод для нахождения высоты параллелепипеда в различных ситуациях.

Пример использования формулы объема

Пример 1: Вычисление объема прямоугольного параллелепипеда

Допустим, у нас есть прямоугольный параллелепипед с длиной l = 5 метров, шириной w = 3 метра и высотой h = 2 метра. Наша задача — найти его объем.

Для этого мы можем использовать формулу объема прямоугольного параллелепипеда:

Объем = длина x ширина x высота

В данном случае, мы можем записать:

Объем = 5 м x 3 м x 2 м

Производные умножение, получаем:

Объем = 30 м³

Таким образом, объем прямоугольного параллелепипеда равен 30 кубическим метрам. Просто, не так ли?

Пример 2: Вычисление объема цилиндра

Давайте рассмотрим другой пример. Представим, что у нас есть цилиндр с радиусом основания r = 2 метра и высотой h = 10 метров. Наша задача — найти его объем.

Для этого мы можем использовать формулу объема цилиндра:

Объем = площадь основания x высота

Это правильно, мы должны сначала найти площадь основания. Формула для вычисления площади основания цилиндра:

Площадь основания = пи x радиус²

Имея все необходимые значения (радиус r = 2 м и высоту h = 10 м), мы можем записать:

Площадь основания = 3.14 x 2²

Площадь основания = 3.14 x 4

Площадь основания = 12.56 м²

Теперь мы можем использовать полученное значение площади основания и высоту, чтобы найти объем цилиндра:

Объем = 12.56 м² x 10 м

Объем = 125.6 м³

Итак, объем цилиндра равен 125.6 кубическим метрам. Ура!

Надеюсь, эти примеры помогли вам лучше понять, как можно использовать формулу объема на практике. Математика может быть интересной и полезной, не так ли? Если у вас есть какие-либо вопросы, не стесняйтесь задавать их!

Важность знания высоты параллелепипеда

Зная высоту параллелепипеда, мы можем рассчитать его объем, определить его форму, а также использовать это понятие в других областях знания, таких как архитектура, машиностроение и геодезия.

Высота параллелепипеда является ключевым показателем для понимания его структуры и свойств. Это значение позволяет нам определить, какая грань является основанием, а какие грани являются боковыми. Это в свою очередь помогает нам рассчитать площадь граней и периметр основания, что может быть полезно для решения различных задач.

Знание высоты параллелепипеда также может быть полезно при решении задач, связанных с объемом тела. Оно позволяет нам определить объем параллелепипеда и сравнивать его с объемом других тел. Это может быть полезно, например, при выборе соответствующего контейнера для хранения или транспортировки предметов.

Итак, знание высоты параллелепипеда играет важную роль в понимании его структуры и свойств, а также позволяет решать различные задачи и применять его в практических ситуациях. Оно является неотъемлемой частью математического образования и имеет широкие применения в различных областях знания. Поэтому важно ознакомиться с понятием высоты параллелепипеда и усвоить его основы.