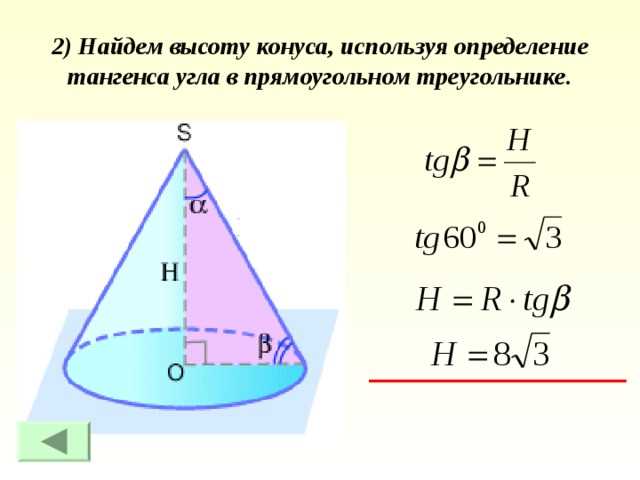
Как найти высоту конуса: формула и примеры расчета по радиусу и образующей
Изучая геометрию, мы всегда сталкиваемся с различными фигурами и формулами для вычисления их размеров. Конус — это одна из таких фигур, которая имеет особенности в определении своих характеристик, включая высоту. Высота конуса — это расстояние от вершины до основания, и она играет важную роль в решении различных задач.
Для нахождения высоты конуса существует формула, которая зависит от данных, которые у нас есть. Одна из наиболее распространенных формул — это использование радиуса и длины образующей. В этом случае мы можем применить теорему Пифагора для нахождения высоты.
Давайте посмотрим на пример расчета высоты конуса используя радиус и образующую. Берем радиус r = 5 см и образующую l = 12 см. Подставляя значения в формулу, получаем h = sqrt(l^2 — r^2) = sqrt(12^2 — 5^2) = sqrt(144 — 25) = sqrt(119) ≈ 10.92 см.
Таким образом, использование формулы для вычисления высоты конуса позволяет нам точно определить этот параметр и применять его в решении задач.
Определение конуса
У конуса есть несколько характеристик, которые помогают нам определить его форму и размеры:
- Радиус основания: это расстояние от центра основания конуса до любой его точки. Обозначается буквой «r».
- Высота: это расстояние от вершины конуса до основания. Обозначается буквой «h».
- Образующая: это отрезок, соединяющий вершину конуса с точкой на его окружности. Обозначается буквой «l».
Важно знать, что высота и образующая конуса образуют прямой угол, то есть они перпендикулярны. Также, радиус основания и образующая связаны друг с другом через теорему Пифагора: r² + h² = l².
Данная формула позволяет нам вычислить одну из величин, если известны две другие. Например, если нам даны радиус основания и образующая конуса, мы можем вычислить его высоту, подставив известные значения в формулу и решив уравнение. То же самое можно сделать, если известны радиус основания и высота.
Теперь, когда мы знаем определение конуса и как его характеристики связаны между собой, давайте рассмотрим примеры расчета высоты конуса с помощью формулы и зададимся вопросом: «Какую высоту имеет конус с радиусом основания 5 и образующей 13?»
| Радиус основания (r) | Образующая (l) | Высота (h) |
|---|---|---|
| 5 | 13 | ? |
Мы знаем, что по теореме Пифагора выполняется соотношение: r² + h² = l². Подставим известные значения и найдем неизвестную величину:
5² + h² = 13²
25 + h² = 169
h² = 144
h = √144
h = 12
Таким образом, высота конуса с радиусом основания 5 и образующей 13 равна 12.
Теперь, когда мы понимаем, как определить конус и рассчитать его высоту с помощью формулы, мы можем применить эти знания на практике и решать задачи по этой теме с легкостью.
Формула для расчета высоты конуса
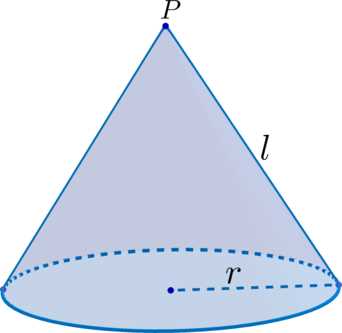
Формула для расчета высоты конуса, основанная на радиусе и образующей, выглядит следующим образом:
h = sqrt(r^2 — l^2)
где:
- h — высота конуса;
- r — радиус основания конуса;
- l — образующая конуса (расстояние от вершины до точки на окружности основания).
Эта формула основана на теореме Пифагора, которая утверждает, что квадрат гипотенузы (в данном случае радиус) равен сумме квадратов катетов (в данном случае высоты и образующей).
| Радиус (r) | Образующая (l) | Высота (h) |
|---|---|---|
| 3 | 5 | 4 |
| 7 | 10 | 8.54 |
| 2.5 | 4.5 | 3.87 |
Например, если радиус основания конуса составляет 3 единицы, а образующая равна 5 единицам, то высота конуса будет 4 единицы. Это можно рассчитать, подставив значения в формулу: h = sqrt(3^2 — 5^2) = sqrt(9 — 25) = sqrt(-16). Но, поскольку невозможно извлечь корень из отрицательного числа, мы получаем невозможное значение для высоты конуса. В этом случае конус будет вырожденным и не будет иметь высоты.
Таким образом, формула для расчета высоты конуса может быть полезна при решении геометрических задач или в практических ситуациях, где необходимо знать высоту конуса на основе его радиуса и образующей.
Примеры расчета высоты конуса
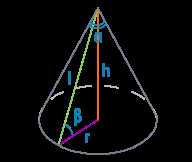
Пример 1:
Найдем высоту конуса, если радиус основания равен 5 и образующая равна 12.
Используем формулу: высота = √(образующая² — радиус²)
Подставляем значения: высота = √(12² — 5²) = √(144 — 25) = √119 ≈ 10.92
Таким образом, высота конуса в данном примере составляет около 10.92.
Пример 2:
Допустим, что известны радиус основания и высота конуса, и нужно найти образующую. Радиус равен 8, а высота равна 15.
В данном случае используем формулу: образующая = √(радиус² + высота²)
Выполняем подстановку: образующая = √(8² + 15²) = √(64 + 225) = √289 = 17
Таким образом, образующая конуса в данном примере составляет 17.
Пример 3:
Рассмотрим ситуацию, когда известны образующая и высота конуса, а надо найти радиус основания. Образующая равна 13, а высота равна 9.
Для решения этой задачи используем формулу: радиус = √(образующая² — высота²)
Подставляем значения: радиус = √(13² — 9²) = √(169 — 81) = √88 ≈ 9.38
Таким образом, радиус основания конуса в данном примере примерно равен 9.38.
Используя соответствующие формулы, легко рассчитать высоту конуса при известных значениях радиуса и образующей, а также находить другие параметры конуса при известных двух параметрах.






