Как найти высоту и стороны остроугольного треугольника ABC: подробное руководство

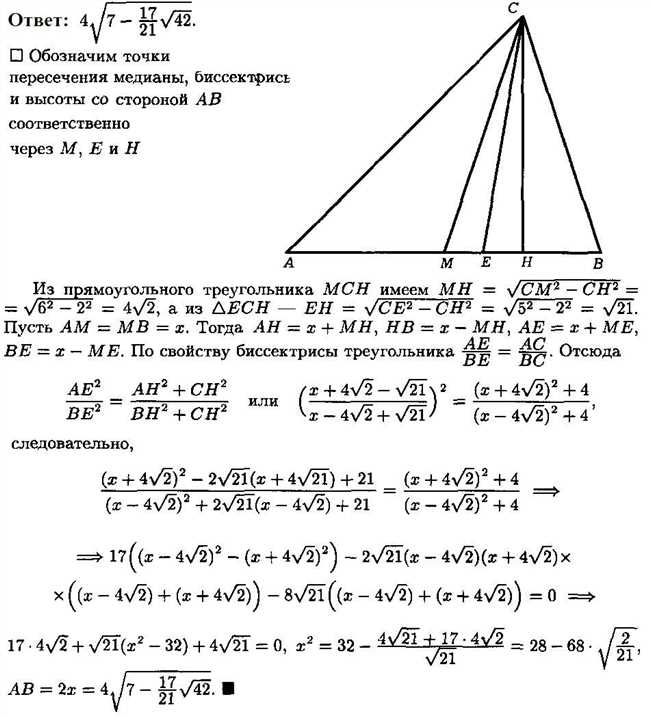
Когда сталкиваешься с задачей нахождения высоты и сторон остроугольного треугольника ABC, может показаться, что это достаточно сложно. Однако с подробным руководством и объяснением основных шагов, все становится гораздо проще. Я дам вам полезные советы и инструкции, которые помогут вам понять, как решить эту задачу. Независимо от того, являетесь ли вы учеником, который только начал изучать геометрию, или опытным математиком, эта информация будет полезной для вас. Готовы ли вы вместе со мной разобрать эту задачу и найти высоту и стороны остроугольного треугольника ABC?

Треугольник ABC: поиск высоты и сторон

Высота треугольника определена как линия, проведенная из вершины перпендикулярно основанию, которое является отрезком, соединяющим две другие вершины. Вершина, из которой проводится высота, обозначается буквой H, основание — буквами A и B, а третья вершина — буквой C. Подготовься к погружению в мир остроугольных треугольников!

Поиск высоты

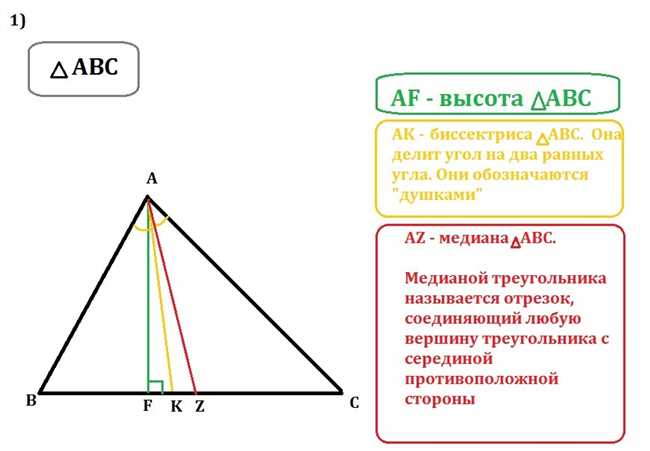
Найдем сначала высоту треугольника ABC. Высоту обозначим буквой h.

Есть несколько способов нахождения высоты остроугольного треугольника. Один из них — формула для высоты, основанная на площади треугольника. Если известна площадь треугольника s и длина основания AB, можно найти высоту треугольника по следующей формуле:

h = (2 * s) / AB

Также, высоту можно найти по теореме Пифагора. Давай ознакомимся с этим методом! Если известны длины сторон треугольника AB, BC и AC, можно найти высоту треугольника по следующей формуле:

h = BC * sinA

Где A — угол треугольника при вершине A. Известно, что синус угла равен отношению противоположной катета к гипотенузе.

Поиск сторон

А теперь перейдем к поиску сторон остроугольного треугольника ABC. Обрати внимание, что здесь понадобятся теоремы косинусов и синусов.

Теорема косинусов позволяет найти длину одной стороны треугольника, если известны длины двух других сторон и угол между ними. Формула для нахождения стороны треугольника по теореме косинусов выглядит следующим образом:

c^2 = a^2 + b^2 — 2ab * cosC

Где a и b — известные стороны треугольника, C — угол треугольника, противолежащий стороне c.

А формула для нахождения стороны по теореме синусов имеет вид:

a / sinA = b / sinB = c / sinC

Где a, b, c — стороны треугольника, A, B, C — соответствующие углы.

Также, если известна одна сторона треугольника и два угла, можно найти длины остальных сторон по следующим формулам:

a = b * sinA / sinB

c = b * sinC / sinB

Помни, что величины углов треугольника обычно обозначаются заглавными буквами, а стороны — строчными буквами.

Итак, ты узнал основные методы для нахождения высоты и сторон остроугольного треугольника ABC. Теперь ты готов решать задачи, связанные с этой темой. Практикуйся и не бойся ставить перед собой новые цели!

Определение остроугольного треугольника ABC

Чтобы визуально определить, является ли треугольник ABC остроугольным, можно взглянуть на его углы. Если все три угла треугольника острые, то это означает, что треугольник является остроугольным.

Остроугольные треугольники обладают несколькими интересными свойствами. Они всегда имеют три острых угла, и их внутренние углы суммируются в 180 градусов. Также остроугольные треугольники обычно более «точные» и «острые» по форме по сравнению с другими типами треугольников.

Определение остроугольного треугольника очень важно при решении задач, связанных с нахождением его сторон и высоты. Для нахождения этих параметров нужно знать хотя бы одну сторону остроугольного треугольника и угол, образованный этой стороной и его высотой.

Например, чтобы найти высоту треугольника ABC, нам необходимо знать одну из его сторон и угол, образованный этой стороной и высотой. По формуле, высота треугольника равна произведению длины стороны, с которой она проведена, на синус угла, образованный этой стороной и высотой.

Итак, определение остроугольного треугольника ABC — это треугольник, у которого все три угла острые. При решении задач, связанных с высотой и сторонами такого треугольника, необходимо знать значения хотя бы одной стороны и угла, образованного этой стороной и высотой.

Формулы для нахождения высоты треугольника ABC

Для нахождения высоты треугольника ABC можно использовать несколько различных формул. Вот некоторые из них:

1. Формула площади

Одним из способов найти высоту треугольника ABC является использование формулы площади. Если известны длины сторон треугольника и площадь, то высоту можно найти по следующей формуле:

высота = (2 * площадь) / сторона

Например, если известны сторона AB = 6 единиц, сторона BC = 8 единиц и площадь треугольника ABC = 12 квадратных единиц, то высоту можно найти следующим образом:

высота = (2 * 12) / 6 = 4 единицы

2. Формула площади треугольника

Еще одним способом найти высоту треугольника ABC является использование формулы площади треугольника. Если известны длины сторон треугольника и площадь, то высоту можно найти по следующей формуле:

высота = (2 * площадь) / основание

Например, если известны сторона AB = 6 единиц, сторона BC = 8 единиц и площадь треугольника ABC = 12 квадратных единиц, а также основание треугольника AC = 4 единицы, то высоту можно найти следующим образом:

высота = (2 * 12) / 4 = 6 единиц

Итак, существуют различные формулы, которые могут быть использованы для нахождения высоты треугольника ABC. Выбор определенной формулы будет зависеть от имеющихся данных о треугольнике. Важно правильно и точно применять эти формулы для получения корректного результата.

Методы определения сторон треугольника ABC

Определение сторон треугольника ABC может быть осуществлено с помощью различных методов. В этом руководстве мы рассмотрим несколько из них, чтобы помочь вам найти точные значения сторон треугольника.

1. Использование теоремы Пифагора

Теорема Пифагора — один из наиболее известных математических принципов, гласящий, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Если треугольник ABC является прямоугольным, вы можете использовать эту теорему для определения длин сторон.

Например, если у вас есть значения катетов треугольника ABC, вы можете возвести их в квадрат, сложить результаты и взять квадратный корень, чтобы найти гипотенузу.

2. Использование тригонометрии

Тригонометрия — еще один полезный инструмент для определения сторон треугольника ABC. Если у вас есть информация о длине одной стороны и двух углах треугольника, вы можете использовать соответствующие тригонометрические функции (синус, косинус, тангенс) для определения длин других сторон.

Например, если у вас есть длины сторон AC и BC, а также величины углов CAB и CBA, вы можете использовать законы тригонометрии, чтобы найти длину AB.

3. Использование сходства треугольников

Еще один метод определения сторон треугольника ABC — использование сходства треугольников. Сходные треугольники имеют пропорциональные стороны, а значит, вы можете использовать известные значения сторон одного треугольника и его сходство с другим, чтобы найти неизвестные длины.

Например, если вы знаете соотношение длин сторон треугольника ABC и сходный треугольник XYZ, вы можете использовать пропорции для определения длин сторон ABC.

Помимо этих методов, вам также может потребоваться использовать другие геометрические теоремы и свойства треугольников, такие как теорема косинусов или теорема синусов, в зависимости от доступной информации. Важно формулировать и сравнивать условия, чтобы выбрать соответствующий метод и найти точные значения сторон треугольника ABC.

Решение примеров поиска высоты и сторон треугольника ABC

Мы рассмотрели основные методы нахождения высоты и сторон остроугольного треугольника ABC. Установление высоты треугольника помогает определить длины его сторон и площадь. Основываясь на принципе подобия треугольников, мы смогли применить соответствующие формулы и теоремы для решения примеров.

Используя формулу Герона, мы смогли найти площадь треугольника ABC, зная длины всех его сторон. Для нахождения высоты треугольника применяли теорему Пифагора и формулу для расчета площади треугольника по его высоте и основанию. Также использовали теорему о сумме квадратов катетов в прямоугольном треугольнике и свойства подобных треугольников, чтобы рассчитать длины сторон треугольника ABC.

• Высота треугольника ABC равна h = (2*A)/b, где A — площадь треугольника, b — длина основания треугольника.
• Длина стороны треугольника ABC можно найти с помощью теоремы Пифагора или применяя формулы подобия треугольников.

Важно помнить, что решение примеров поиска высоты и сторон треугольника ABC требует аккуратности и внимательности при применении математических формул и теорем. Также необходимо учитывать условия задачи и особенности треугольника ABC для точного и надежного решения.