
Когда мы работаем с треугольниками, обычно нам требуется найти углы между сторонами. Нахождение угла между катетом и гипотенузой — одна из основных задач, с которой мы сталкиваемся при решении геометрических задач. Чтобы найти этот угол, мы можем использовать основные свойства тригонометрии и теорему Пифагора. В данной статье я подробно объясню, как найти угол между катетом и гипотенузой, и приведу несколько примеров для лучшего понимания. Это знание будет полезно при решении задач и построении треугольников в различных сферах науки и практики. Не волнуйтесь, это несложно, и мы вместе разберемся!
Определение и свойства катета и гипотенузы
Катеты — это два отрезка, примыкающих к прямому углу в треугольнике. Они располагаются внутри треугольника и соединяются с вершиной прямого угла. В прямоугольном треугольнике всегда есть два катета, и они всегда равны по длине.
Гипотенуза — это самая длинная сторона прямоугольного треугольника, которая лежит напротив прямого угла. Гипотенуза является противоположной стороной прямого угла и обычно является наибольшей стороной треугольника.
Основные свойства катета и гипотенузы:
- Катеты прямоугольного треугольника всегда перпендикулярны друг другу.
- Длина гипотенузы всегда больше длины каждого из катетов.
- Катеты и гипотенуза являются пропорциональными сторонами треугольника.
Важно понимать, что катеты и гипотенуза взаимосвязаны и не могут существовать отдельно друг от друга. Они образуют основу прямоугольного треугольника и служат основой для вычисления его углов и сторон.
Теперь, когда вы знаете определение и свойства катета и гипотенузы, вам будет легче работать с прямоугольными треугольниками и находить углы между катетом и гипотенузой.
Теорема Пифагора
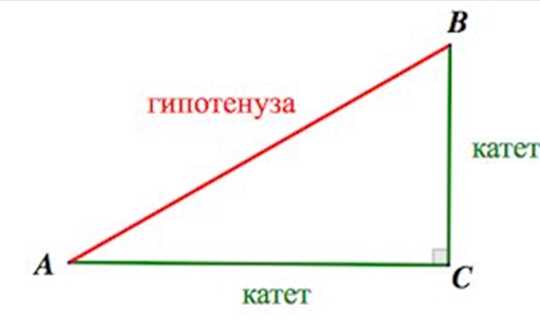
Для более понятного объяснения теоремы Пифагора, представим себе прямоугольный треугольник с катетами a и b, и гипотенузой c. Теорему можно записать следующим образом:
c² = a² + b²
Интуитивно понятно, что когда мы возводим каждую сторону треугольника в квадрат и складываем их, полученная сумма будет равна квадрату гипотенузы. Это вполне логично, потому что гипотенуза является наибольшей из трех сторон и образует прямой угол с катетами.
Теорема Пифагора имеет множество практических применений в реальной жизни. К примеру, она используется в строительстве для определения длины диагонали, когда известны ширина и высота прямоугольника. Также она применяется в тригонометрии для расчета углов и сторон треугольников.
Давайте рассмотрим пример. У нас есть прямоугольный треугольник, в котором катет a равен 3, а катет b равен 4. Найдем длину гипотенузы с помощью теоремы Пифагора:
c² = 3² + 4² = 9 + 16 = 25
Получается, что квадрат гипотенузы равен 25. Извлекая квадратный корень, мы получим:
c = √25 = 5
Таким образом, длина гипотенузы в данном примере равна 5. Мы можем убедиться в правильности нашего решения, проведя замер с помощью линейки.
Таким образом, теорема Пифагора является фундаментальным инструментом при работе с прямоугольными треугольниками. Она позволяет нам находить длину неизвестной стороны, если известны две другие. Знание и применение этой теоремы позволят вам с легкостью решать геометрические задачи и применять ее в реальной жизни.
Формула нахождения угла между катетом и гипотенузой
В математике существует специальная формула, которая позволяет находить угол между катетом и гипотенузой в прямоугольном треугольнике. Эта формула основана на тригонометрических функциях и называется тангенсом.
Тангенс угла в прямоугольном треугольнике определяется как отношение противолежащего катета к прилежащему катету. Используя эту формулу, можно выразить угол между катетом и гипотенузой следующим образом:
Тангенс угла между катетом и гипотенузой = противолежащий катет / прилежащий катет
Применительно к конкретной задаче, угол между катетом и гипотенузой можно рассчитать, используя следующий алгоритм:
- Определите длину противолежащего катета и длину прилежащего катета.
- Разделите длину противолежащего катета на длину прилежащего катета, чтобы найти тангенс угла.
- Используя таблицу значений тангенса или калькулятор, найдите значение угла, соответствующее полученному значению тангенса.
Например, если длина противолежащего катета равна 4, а длина прилежащего катета равна 3, то тангенс угла между катетом и гипотенузой будет равен 4/3. Подставляя это значение в таблицу значений тангенса или используя калькулятор, мы можем узнать, что угол примерно равен 53 градусам.
| Тангенс угла | Угол (градусы) |
|---|---|
| 0.2679 | 15 |
| 0.5774 | 30 |
| 1 | 45 |
| 1.7321 | 60 |
| 3.7321 | 75 |
| 7.1154 | 85 |
Помните, что результаты рассчетов с использованием тангенса могут быть приблизительными, поскольку таблицы значений ограничены. Если вам требуется большая точность, рекомендуется использовать калькулятор или специализированный математический софт. Также имейте в виду, что в отрицательных углах синусы и косинусы меняются по знаку.
Примеры решения задач
Ниже приведены несколько примеров задач, связанных с поиском угла между катетом и гипотенузой, и подробные объяснения, как их решить.
Пример 1:
Найти угол ABC, если катет AB равен 5 см, а гипотенуза AC равна 10 см.
Решение:
- Используем тригонометрическую функцию синус, так как у нас есть катет и гипотенуза.
- Синус угла ABC равен отношению длины катета AB к длине гипотенузы AC: sin(ABC) = AB / AC = 5 / 10 = 0.5.
- Используя таблицу значений синуса, находим значение угла ABC, ближайшее к 0.5. В данном случае, sin^-1(0.5) = 30°.
Пример 2:
Найти угол DEF, если катет DE равен 8 м, а гипотенуза DF равна 10 м.
Решение:
- Используем тригонометрическую функцию косинус, так как у нас есть катет и гипотенуза.
- Косинус угла DEF равен отношению длины катета DE к длине гипотенузы DF: cos(DEF) = DE / DF = 8 / 10 = 0.8.
- Используя таблицу значений косинуса, находим значение угла DEF, ближайшее к 0.8. В данном случае, cos^-1(0.8) = 36.87°.
Пример 3:
Найти угол GHI, если катет GH равен 6 см, а гипотенуза HI равна 3 см.
Решение:
- Этот пример не имеет физического смысла, так как катет не может быть больше гипотенузы.
- Если возникают такие противоречивые данные, задача не имеет верного решения.
| Угол (в градусах) | Синус | Косинус |
|---|---|---|
| 0° | 0 | 1 |
| 30° | 0.5 | 0.866 |
| 45° | 0.707 | 0.707 |
| 60° | 0.866 | 0.5 |
| 90° | 1 | 0 |






