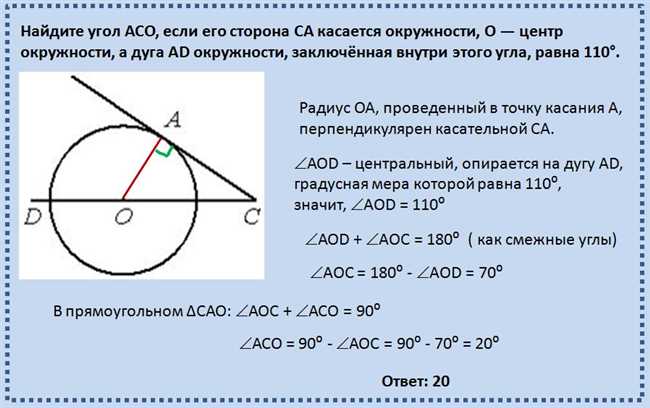
Когда дело касается нахождения угла АСО, когда сторона СА касается окружности, необходимо иметь в виду несколько шагов, чтобы получить точный результат. В этом пошаговом руководстве я расскажу, как это сделать. Первым шагом будет использование данной информации и геометрических свойств для определения меры угла, который мы ищем. Затем мы применим теорему, которая поможет нам связать найденный угол с другими углами в фигуре. И, наконец, используя уравнения околоугольной дуги, мы сможем найти конечное значение угла АСО. Следуя этим шагам, вы сможете легко и точно найти угол АСО в ситуации, когда сторона СА касается окружности.
Шаг 1: Определение известных величин

Прежде чем мы начнем наше пошаговое руководство по определению угла АСО, важно понять, что именно мы знаем о данной геометрической фигуре и какие величины нам известны.
В случае, когда сторона СА касается окружности, зная некоторые известные величины, мы сможем определить угол АСО. В этом случае мы должны знать длину стороны СА и радиус окружности.
Пусть сторона СА имеет длину r, а радиус окружности равен R. Также предположим, что угол АСО обозначен как α.
Теперь, когда мы знаем известные величины, перейдем к следующему шагу, где мы будем использовать эти данные для нахождения угла АСО.
Шаг 2: Применение теоремы касательной
Теперь, когда мы знаем, что сторона СА касается окружности, можем применить теорему касательной.
Теорема касательной утверждает, что линия, проведенная от точки касания на окружности до центра, перпендикулярна к касательной. Это означает, что линия СО является перпендикулярной к стороне СА.
Теперь нам нужно найти меру угла САО, который образуется между линиями СА и СО. Мы можем использовать свойства перпендикуляров, чтобы найти этот угол.
Угол между перпендикулярными линиями равен 90 градусам. Таким образом, угол САО равен 90 градусам, или может быть выражен как альтернативный угол к углу, образованному стороной СА и хордой АО.
Таким образом, угол АСО равен 90 градусам.
Шаг 3: Вычисление угла АСО
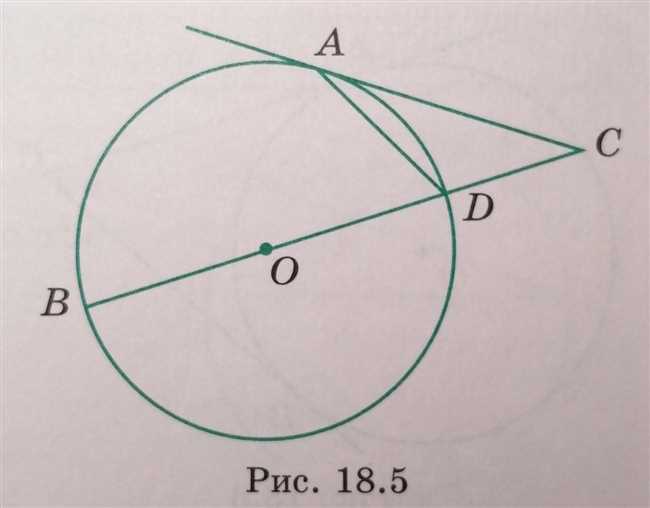
Теперь, когда мы знаем длину стороны СА и радиус окружности, мы можем использовать теорему косинусов для вычисления угла АСО.
Теорема косинусов гласит:
В треугольнике ABC с длинами сторон a, b и c и углом C противолежащим стороне c:
c² = a² + b² — 2ab cos(C)
В нашем случае сторона АС равна радиусу окружности, которую обозначим как r. Сторона СО равна длине скорости, которую обозначим как l. Угол АСО обозначим как θ.
Мы знаем, что радиус окружности противолежит углу АСО, поэтому сторона СА будет соответствовать стороне a, радиусу r будет соответствовать сторона b, а длине скорости l будет соответствовать стороне c.
Теперь мы можем записать уравнение:
r² = l² + l² — 2l * l * cos(θ)
Решая это уравнение относительно угла θ, мы найдем размер угла АСО.
В следующем шаге мы рассмотрим методы решения этого уравнения и вычислим угол АСО.






