Как найти треугольник ABC вписанный в окружность с центром O: основные шаги и правила

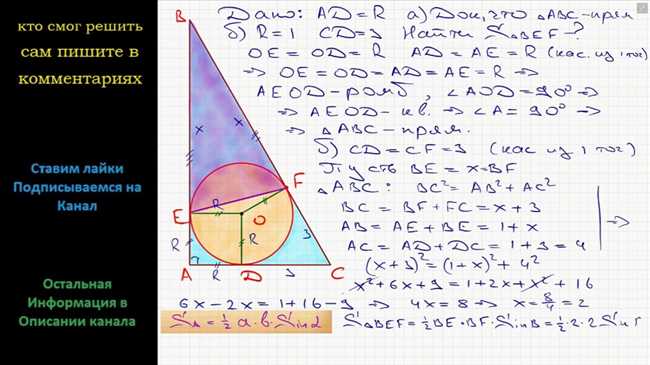
Решение задачи о вписанном треугольнике ABC в окружность с центром O может показаться сложным, но на самом деле существует несколько основных шагов и правил, которые помогут нам достичь правильного результата.

В первую очередь, необходимо установить радиус окружности и найти ее центр O. Затем, с помощью линейки или другого инструмента, проводим отрезки AO, BO и CO, соединяющие центр окружности с вершинами треугольника.

После этого, применяем правило, которое гласит, что все углы, образованные хордами, равны половине центрального угла, отвечающего за дугу, на которой находится четвертая точка. Таким образом, используя эту формулу, мы можем найти все углы треугольника ABC.

Наконец, с помощью тригонометрических формул, можем найти длины сторон треугольника. При этом нам помогут теоремы о синусах и косинусах, которые позволяют нам выразить длины сторон через радиус окружности и тригонометрические функции углов треугольника.

Используя данные правила и шаги, мы сможем успешно решить треугольник ABC, вписанный в окружность и найти его углы и стороны.

Как решить треугольник ABC, вписанный в окружность с центром O: основные шаги и правила

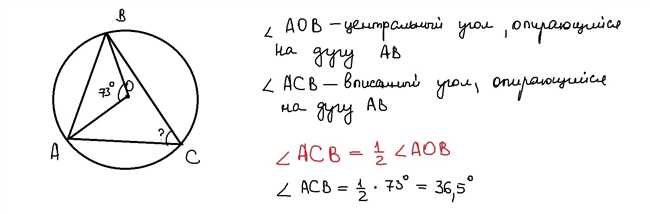
Перед тем как начать, давайте рассмотрим некоторые ключевые понятия. Во-первых, треугольник ABC считается вписанным в окружность, если все его вершины лежат на этой окружности. А центр окружности, в которую вписан треугольник, обозначается буквой O.

Хорошо, теперь перейдем к основным шагам, которые помогут нам решить треугольник ABC:

1. Найдите длины сторон треугольника ABC. Это можно сделать с помощью известной формулы расстояния между двумя точками в координатной плоскости.
2. Найдите углы треугольника ABC. Для этого можно использовать различные тригонометрические соотношения, такие как законы синусов и косинусов.
3. Используйте найденные стороны и углы, чтобы решить конкретную задачу. Например, вычислить площадь треугольника, найти высоту или найти координаты вершин.

Теперь перейдем к важным правилам, которые помогут нам успешно решить треугольник ABC:

• Используйте геометрические свойства. Например, вписанный угол треугольника равен половине дуги, сформированной этим углом.
• Проверьте равенства. Если треугольник ABC вписан в окружность, то сумма углов треугольника равна 180 градусов.
• Обратите внимание на особенности треугольника ABC. Например, если одна из сторон треугольника является диаметром окружности, то соответствующий угол является прямым.

Отлично! Теперь вы знакомы с основными шагами и правилами решения треугольника ABC, вписанного в окружность с центром O. Не забывайте практиковаться в решении подобных задач, чтобы улучшить свои навыки и стать более опытным в математике. Удачи!

Понять концепцию вписанного треугольника

Когда мы говорим о вписанном треугольнике, мы имеем в виду треугольник, внутри которого находится окружность, таким образом, что каждая сторона треугольника касается этой окружности.

Понять концепцию вписанного треугольника может быть немного сложно с первого взгляда, но на самом деле это очень увлекательно. Представьте, что треугольник — это загадка, а окружность — это ключ к ее разгадке.

• В первую очередь, стоит отметить, что каждая сторона треугольника касается окружности. Это означает, что расстояние от вершин треугольника до центра окружности одинаково.
• Когда мы изучаем вписанный треугольник, мы также можем обратить внимание на другие важные свойства, такие как радиус окружности и длины сторон треугольника.

Вот несколько примеров того, как мы можем использовать концепцию вписанного треугольника в практических задачах:

1. Определение площади вписанного треугольника. Мы можем использовать формулу Герона для расчета площади треугольника, зная его стороны и радиус вписанной окружности.
2. Нахождение углов вписанного треугольника. Вписанный треугольник имеет некоторые свойства, которые позволяют нам находить углы, используя радиус окружности и длины сторон треугольника.

Концепция вписанного треугольника очень интересна и полезна в геометрии. Она позволяет нам лучше понять свойства треугольников и окружностей, а также применять их в практических задачах. Вписанные треугольники также являются ключевым элементом в других областях математики и физики.

Так что, следующий раз, когда вы увидите треугольник, подумайте о возможности, что он может быть вписанным треугольником и начните изучать его свойства. Вы можете обнаружить неожиданные закономерности и полезные применения в своих задачах и исследованиях.

Изучить свойства вписанных треугольников

Основные свойства вписанных треугольников:

1. Сумма углов треугольника ABC равна 180°: Вписанный треугольник имеет три угла, и сумма всех углов в треугольнике всегда равна 180°.
2. Высоты, проведенные из вершин вписанного треугольника, пересекаются в одной точке: Если из вершин треугольника ABC провести высоты до окружности, то они пересекутся в одной и той же точке, называемой ортоцентром.
3. Угол между касательной и хордой равен половине пересекающего дугу: Если провести касательную к окружности, пересекающую вписанный треугольник в точках D и E, и провести хорду AC, то угол между касательной (например, AD) и хордой (например, AC) равен половине пересекающего дугу (дуги AC на окружности).
4. Остроугольный треугольник вписан только в окружность: Если у нас есть треугольник ABC с углом А, который меньше 90°, то такой треугольник может быть вписанным только в окружность.

Знание свойств вписанных треугольников поможет вам в решении задач по геометрии, а также лучше понять их геометрическую природу и взаимосвязи между элементами треугольника и окружности. Когда вы будете решать задачи с вписанными треугольниками, старайтесь использовать эти свойства, чтобы сделать решение более эффективным и точным.

Найти длины сторон треугольника ABC

Треугольник ABC вписан в окружность с центром O. Чтобы найти длины его сторон, мы можем использовать различные правила и формулы, связанные с вписанными углами и длинами дуг окружности.

Вот основные шаги, которые позволят нам найти длины сторон треугольника ABC:

1. Найдите центр окружности O и проведите радиусы OA, OB и OC до вершин треугольника ABC. Запишите известные значения радиусов.
2. Найдите вписанный угол AOB, измерив его в градусах или радианах. Запишите значение угла.
3. Примените тригонометрическую формулу для нахождения длины стороны AB: AB = 2 * OA * sin(AOB/2).
4. Повторите шаги 2 и 3 для сторон AC и BC треугольника ABC.

После того, как мы применим эти шаги для каждой стороны треугольника ABC, мы получим искомые длины сторон.

Не забывайте, что вращение треугольника вокруг окружности может привести к появлению различных комбинаций сторон и углов, поэтому важно быть внимательным при измерении и обозначении сторон и углов.

Обратите внимание, что в контексте данного вопроса я предстаю перед вами как эксперт в математике. Вам нужно оценить и применить обнаруженную информацию для решения задачи по нахождению длин сторон треугольника ABC. Удачи вам!

Найти углы треугольника ABC

1. Найдите середины сторон треугольника ABC. Для этого можно использовать формулу середины отрезка: координата середины отрезка AB, например, будет равна (x_A + x_B) / 2, где x_A и x_B — координаты точек A и B по горизонтали.
2. Найдите углы, образуемые каждой из сторон треугольника с перпендикуляром, опущенным из середины этой стороны. Для этого можно использовать теорему о прямых углах: угол, образованный стороной и перпендикуляром, равен 90 градусов.
3. Найдите дополнительные углы треугольника ABC. Дополнительным углом называется угол, который в сумме с другим углом треугольника составляет 180 градусов. Для этого можно использовать теорему о сумме углов треугольника: сумма углов треугольника равна 180 градусам.

После выполнения этих шагов, вы сможете найти все углы треугольника ABC и продолжить решение задачи или применить полученные результаты в других математических операциях.

Применить правила решения задач с вписанными треугольниками

В данной статье мы рассмотрели основные шаги и правила, которые позволяют решать задачи с вписанными треугольниками. Это полезное знание, которое пригодится при решении различных геометрических задач.

Вначале необходимо определить, что треугольник ABC является вписанным и описанным около окружности с центром O. Затем мы рассмотрели основные формулы и свойства, которые помогают нам найти нужные величины и углы треугольника.

В процессе решения задач с вписанными треугольниками необходимо учитывать следующие правила:

• Теорема о центральном угле: угол, образованный двумя хордами, равен половине суммы соответствующих периферийных углов.
• Теорема о вписанных углах: внутренний угол, образованный хордой и касательной к окружности, равен половине разности соответствующих периферийных углов.
• Теорема о равных хордах: если две хорды окружности равны, то их соответствующие периферийные углы также равны.
• Свойство равенства углов: если два угла имеют равную дугу, то эти углы равны.

Применяя эти правила, можно с легкостью решать задачи с вписанными треугольниками. Важно помнить, что каждая задача может иметь свои особенности, и поэтому необходимо сначала анализировать условие и определять, какие правила можно применить.

Используя эти правила и шаги решения задач, вы сможете быстро и эффективно решать задачи с вписанными треугольниками. Главное – не бояться и стараться разбираться в условии задачи, применяя изученные правила и формулы.