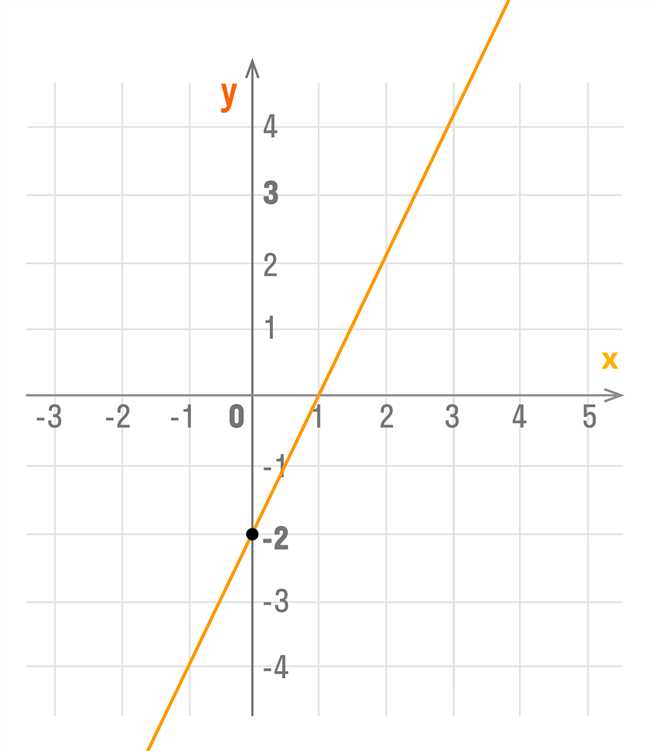
Когда мы сталкиваемся с системой двух или более линейных уравнений, найти их точку пересечения может быть вызовом. Но не отчаивайтесь – существует пошаговая инструкция, которая поможет вам решить эту задачу без необходимости строить графики.
Первый шаг – привести уравнения к стандартному виду. Затем, используя метод замены или метод комбинирования, исключите одну переменную из уравнений. Найдите значение этой переменной и подставьте его в одно из уравнений, чтобы найти значение другой переменной.
Таким образом, получив значения обоих переменных, вы найдете точку пересечения линейных функций. Этот метод позволяет решить систему уравнений более эффективно и точно, несмотря на отсутствие построения графиков.
Запишите уравнения линейных функций в стандартной форме
Стандартная форма уравнения линейной функции имеет вид:
Ax + By = C
где A, B и C — коэффициенты, а x и y — переменные.
Чтобы записать уравнение в стандартной форме, необходимо выполнить следующие шаги:
- Упорядочьте все члены так, чтобы все переменные оказались слева от знака равенства, а все константы — справа.
- Поместите все члены, содержащие переменную x, налево от знака равенства, а все остальные — направо.
- Если переменная y отсутствует в уравнении, то коэффициент B будет равен нулю.
- Если коэффициенты A и B делятся на одно и то же число, можно разделить все коэффициенты на это число, чтобы упростить уравнение.
Примеры уравнений в стандартной форме:
3x — 2y = 5
-4x + 7y = 2
Когда у вас есть два уравнения в стандартной форме, вы можете найти точку пересечения, решив эту систему уравнений. Это может быть сделано путем метода подстановки или метода комбинирования, но это уже другая тема для обсуждения.
Решение системы уравнений методом подстановки или методом сложения/вычитания
Метод подстановки
Для начала, возьмем два уравнения системы и решим одно из них относительно одной переменной. Затем, найденное значение переменной подставим в другое уравнение и решим его. Полученное значение переменной будет являться одной из координат точки пересечения.
Давайте посмотрим на пример:
У нас есть система уравнений:
2x + 3y = 10
x — y = 4
Выберем второе уравнение и решим его относительно переменной x:
x = y + 4
Теперь возьмем этот результат и подставим его в первое уравнение:
2(y + 4) + 3y = 10
Раскроем скобки и решим уравнение:
2y + 8 + 3y = 10
5y + 8 = 10
5y = 2
y = 2/5
Теперь, чтобы найти значение x, подставим найденное значение y в одно из исходных уравнений:
x — (2/5) = 4
x = 4 + 2/5
x = 22/5
Таким образом, точка пересечения линейных функций будет иметь координаты (22/5, 2/5).
Метод сложения/вычитания
Еще один способ решить систему уравнений — метод сложения/вычитания. Суть этого метода заключается в том, что мы складываем или вычитаем уравнения друг из друга так, чтобы одна из переменных исчезла.
Просмотрим наш пример снова:
У нас есть система уравнений:
2x + 3y = 10
x — y = 4
Умножим второе уравнение на 2, чтобы избавиться от коэффициента перед переменной x:
2(x — y) = 2 * 4
2x — 2y = 8
Теперь сложим это уравнение с первым уравнением:
(2x + 3y) + (2x — 2y) = 10 + 8
4x + y = 18
Мы получили новое уравнение, в котором осталась только одна переменная. Теперь решим его относительно этой переменной:
y = 18 — 4x
Теперь подставим это значение y в одно из исходных уравнений:
x — (18 — 4x) = 4
x — 18 + 4x = 4
5x = 22
x = 22/5
Осталось только найти значение y, подставив найденное значение x в уравнение:
y = 18 — 4(22/5)
y = 2/5
Итак, точка пересечения линейных функций имеет координаты (22/5, 2/5).
Вот и все! Мы решили систему уравнений методом подстановки и методом сложения/вычитания. Эти два метода помогают найти точку пересечения линейных функций без построения графиков. Будьте внимательны при решении уравнений и не бойтесь экспериментировать!
Заключение
Если вы следовали пошаговой инструкции и правильно решили систему уравнений с линейными функциями, то на этом этапе вам остается проверить полученное решение.
Для этого необходимо подставить найденные значения обратно в исходные уравнения и убедиться, что они обе станут верными. Если после подстановки значения необходимых переменных в оба уравнения, оба уравнения останутся верными, значит, вы правильно нашли точку пересечения линейных функций.






