Как найти точки по координатам: основные советы и пошаговая инструкция для новичков

Как найти точки по координатам: советы и инструкции для начинающих

Вы, вероятно, сталкивались с ситуацией, когда вам нужно было найти определенную точку по ее координатам на карте или плане. Может быть, вы хотите найти место встречи с друзьями или знать, как добраться до определенного места. Но как найти точку по ее координатам? Не волнуйтесь, в этой статье мы расскажем вам о нескольких способах найти точки по координатам. Мы поделимся с вами советами и инструкциями, которые помогут вам сориентироваться и успешно найти желаемую точку. Будьте внимательны и следуйте инструкциям, и вы сможете без проблем найти точку по ее координатам!

Точки по координатам: советы и инструкции для начинающих

Когда вы ориентируетесь на карте или находитесь на каком-то месте, вы наверняка слышали о понятии «широта и долгота». Это способ представления координат на поверхности Земли. Широта измеряет расстояние от точки до экватора и обозначается градусами северной или южной широты. Долгота, в свою очередь, измеряет расстояние от точки до меридиана и обозначается градусами восточной или западной долготы.

Конечно, для обычного человека, начинающего запоминать координаты, широта и долгота может показаться сложным и непонятным понятием. Но это совсем не так! Ведь мы каждый день используем карты и навигационные приложения на своих смартфонах. Если вы когда-либо пытались найти определенную точку или задать свое местоположение, то, скорее всего, вам приходилось работать с координатами. Нет, это совсем не страшно и сложно!

Теперь, когда мы поняли, что такое координаты и как их применять на практике, давайте рассмотрим, как можно найти точку по заданным координатам.

Существует несколько способов определить точку по координатам. Вот некоторые из них:

• Использование карты или навигационного приложения: введите координаты в поисковую строку и приложение покажет вам точное местоположение.
• Использование GPS-навигатора: введите координаты в навигатор и он автоматически построит оптимальный маршрут до указанной точки.
• Использование онлайн-карт или сервисов: множество интернет-ресурсов позволяют вам ввести координаты и найти соответствующую точку на карте.

Интересно, какую из этих опций вы предпочитаете? Каждый из них имеет свои преимущества и может быть полезен в определенных ситуациях.

Найдите точку на карте и проследите своим пальцем по пути до нее — это захватывающее и увлекательное приключение! Задумайтесь, какое великолепие таит в себе каждая точка нашей планеты. Каждое место имеет свою историю, свое значение и красоту.

Научитесь использовать координаты, и каждая точка будет для вас открытием, возможностью увидеть и познать что-то новое. Не бойтесь идти в неизвестность, ведь, как говорится, «истинное приключение начинается там, где заканчивается карта».

Что такое координаты и зачем они нужны

Зачем нам нужны координаты? Как часто обращаемся к навигатору, чтобы найти нужный адрес? Или как часто пользуемся картой, чтобы найти определенное место? Все это возможно благодаря координатам. Они позволяют нам точно определить местоположение и перемещаться по пространству.

Координаты также необходимы в научных исследованиях, где часто требуется точно указать положение объектов или проводить измерения. Например, в астрономии координаты звезд позволяют исследователям отслеживать их движение и составлять карты неба. В геодезии координаты используются для создания карт и определения границ земельных участков.

Координаты также применяются в мультимедиа и компьютерных играх. Они позволяют разработчикам создавать виртуальные миры с реалистичной графикой и 3D-эффектами. Игроки могут перемещаться по этим мирам и взаимодействовать с объектами, используя координаты.

В общем, координаты – это инструмент, который помогает нам находиться и перемещаться в пространстве, определять положение объектов и проводить научные исследования. Без них было бы сложно представить себе наше современное мироустройство и развитие науки и техники. Так что следующий раз, когда вы воспользуетесь навигатором или картой, вспомните, как важны и полезны координаты!

Как определить координаты точки на плоскости

Итак, как же мы можем определить координаты точки на плоскости? На самом деле, это довольно просто, если мы знаем две важные вещи: оси координат и систему координат.

Оси координат

На плоскости мы имеем две оси координат — ось X и ось Y. Ось X расположена горизонтально, а ось Y — вертикально. Каждая из осей имеет свое начало, которое называется началом координат. В обозначениях обычно используются буквы O для начала координат, X для оси X и Y для оси Y.

Теперь представьте, что вы идете по графику функции или шкале на карте. Вы смотрите на точку, о которой вам нужно знать координаты. Представьте, что вы находитесь в начале координат и отметьте это место на плоскости.

Обратите внимание на расположение точки относительно осей X и Y. Если точка находится выше оси X, значит, ее Y-координата будет положительной. Если точка находится ниже оси X, тогда ее Y-координата будет отрицательной.

Аналогично, если точка находится правее оси Y, ее X-координата будет положительной, а если она находится левее оси Y, тогда ее X-координата будет отрицательной.

Система координат

Уже понимая оси координат, теперь перейдем к системе координат. Система координат — это способ описания местоположения точки на плоскости с помощью двух чисел — X-координаты и Y-координаты.

Система координат состоит из двух числовых осей, которые пересекаются в начале координат. Поэтому для определения координаты точки нужно указать ее расстояние по оси X (горизонтально) и по оси Y (вертикально) от начала координат.

Итак, чтобы определить координаты точки на плоскости, сначала установите начало координат и нарисуйте оси X и Y. Затем определите, где находится точка относительно осей X и Y, чтобы выразить ее координаты.

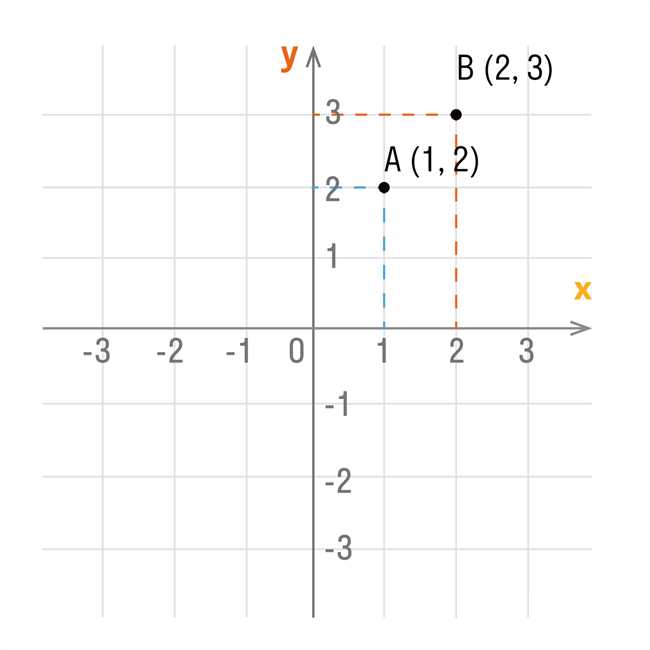
Например, если точка находится две единицы правее оси Y и три единицы выше оси X, то ее координаты будут (2, 3).

Примеры расчета координат точек

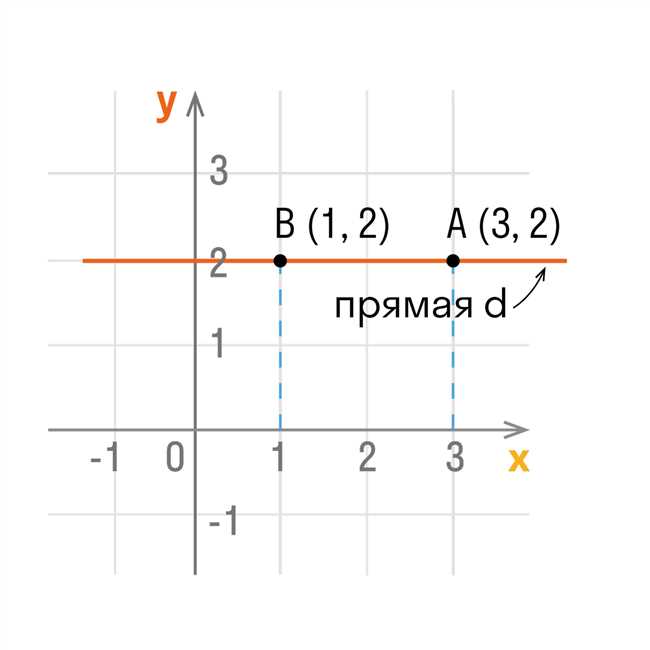
Давайте рассмотрим несколько примеров для лучшего понимания.

Пример 1: Если точка находится на оси X, то ее Y-координата будет равна 0. Например, точка с координатами (5, 0) находится на оси X.

Пример 2: Если точка находится на оси Y, то ее X-координата будет равна 0. Например, точка с координатами (0, -3) находится на оси Y.

Пример 3: Если точка находится в верхнем правом квадранте, то обе ее координаты будут положительными. Например, точка с координатами (2, 4) находится в верхнем правом квадранте.

Пример 4: Если точка находится в нижнем левом квадранте, то обе ее координаты будут отрицательными. Например, точка с координатами (-3, -1) находится в нижнем левом квадранте.

Теперь у вас есть базовое понимание того, как определить координаты точки на плоскости. Упражняйтесь в этом навыке, решайте задачи и вы сможете мгновенно определить местоположение любой точки!

Прямоугольные координаты и полярные координаты

Прямоугольные координаты

Прямоугольные координаты — это наиболее распространенная и привычная система координат. В этой системе каждой точке на плоскости сопоставляются два числа — абсцисса (x) и ордината (y). Абсцисса определяет положение точки на горизонтальной оси, а ордината — на вертикальной оси.

Прямоугольные координаты позволяют точно указать положение точки на плоскости. Например, если у нас есть точка A с координатами (3, 4), то это означает, что она находится на расстоянии 3 единицы от начала координат по горизонтальной оси и на расстоянии 4 единицы по вертикальной оси.

Чтобы наглядно представить точку с прямоугольными координатами, мы можем построить координатную плоскость, где горизонтальная ось (ось x) соответствует абсциссе, а вертикальная ось (ось y) — ординате. Точка A с координатами (3, 4) будет находиться в правом верхнем квадранте.

Полярные координаты

Полярные координаты тоже широко используются в математике и физике, особенно при описании круговых и радиальных движений.

В полярной системе координат каждой точке на плоскости сопоставляются два числа — радиус (r) и угол (θ). Радиус указывает расстояние от начала координат до точки, а угол определяет направление от начала координат к точке.

Угол в полярных координатах измеряется в радианах. Положительное направление угла совпадает с направлением против часовой стрелки, а отрицательное — с направлением по часовой стрелке.

Чтобы полностью описать точку в полярных координатах, мы указываем радиус и угол. Например, точку B можно представить в полярных координатах как (2, π/3), что означает, что она находится на расстоянии 2 единицы от начала координат и образует угол π/3 с положительным направлением оси x.

Графическое представление точек с полярными координатами кажется сложным, но на самом деле оно имеет свою простоту. Если мы нарисуем радиус от начала координат к точке B и затем проведем линию, перпендикулярную этому радиусу и проходящую через точку B, то получим круговой график.

Чтобы перейти от прямоугольных координат к полярным и наоборот, мы можем использовать следующие формулы:

• Прямоугольные координаты в полярные:
  1. r = sqrt(x^2 + y^2)
  2. θ = arctan(y / x)
• Полярные координаты в прямоугольные:
  1. x = r * cos(θ)
  2. y = r * sin(θ)

Таким образом, прямоугольные и полярные координаты являются двумя разными способами описания положения точек на плоскости. Обе системы имеют свои преимущества и могут быть полезны в различных областях математики и физики. Знание и понимание этих систем координат помогут вам лучше ориентироваться в пространстве и решать задачи, связанные с координатами точек.

Как найти расстояние между двумя точками

Вы когда-нибудь задумывались, как найти расстояние между двумя точками? Интересно, не правда ли? Ну, я рад сообщить вам, что это на самом деле совсем несложно! Для начала, давайте вспомним некоторые базовые понятия из геометрии.

Вам, вероятно, знакомо понятие «координаты». Каждая точка на плоскости или в пространстве может быть представлена собой парой или тройкой чисел (в зависимости от размерности пространства). Координаты точки определяют ее положение относительно начала координат.

Теперь давайте перейдем к самой задаче — нахождению расстояния между двумя точками. Для этого мы будем использовать теорему Пифагора. Вы наверняка слышали о ней во время занятий геометрией в школе, не так ли?

Итак, представьте себе две точки, которые мы обозначим как (x1, y1) и (x2, y2). Чтобы найти расстояние между ними, мы должны найти разность между их координатами по оси x и по оси y. Затем мы возведем эти разности в квадраты, сложим их и извлечем квадратный корень из результата.

Вот формулы, которые помогут нам найти расстояние между точками:

• Разность по оси x: x2 — x1
• Разность по оси y: y2 — y1
• Расстояние между точками: √[(x2 — x1)² + (y2 — y1)²]

Очень просто, не так ли? Теперь давайте рассмотрим пример, чтобы увидеть всё это в действии. Представьте себе, что у нас есть две точки с координатами (2, 3) и (5, 7). В числах это выглядит так:

x1 = 2, y1 = 3

x2 = 5, y2 = 7

Подставим эти значения в формулу:

Разность по оси x: 5 — 2 = 3

Разность по оси y: 7 — 3 = 4

Расстояние между точками: √[(3)² + (4)²] = √[9 + 16] = √25 = 5

Таким образом, расстояние между точками (2, 3) и (5, 7) равно 5.

Вот и все! Вы только что научились находить расстояние между двумя точками с помощью формулы и теоремы Пифагора. Эти знания будут полезными для решения различных геометрических задач и применения в практической деятельности.

Теперь, когда у вас есть эти знания, вы можете использовать их, чтобы решать задачи связанные с нахождением расстояния между точками. Попробуйте сами решить некоторые упражнения и посмотрите, насколько хорошо они у вас получаются!

Заключение

В этой статье мы рассмотрели основные принципы работы с координатами и дали несколько советов и инструкций для тех, кто только начинает знакомиться с этой темой. Мы рассмотрели как находить точки по координатам на плоскости, а также на координатной оси.

Надеемся, что эта информация была полезной и поможет вам лучше понимать и использовать координаты в геометрических задачах. Не бойтесь экспериментировать и применять полученные знания на практике – это поможет вам развить навыки работы с координатами и достичь успеха в изучении геометрии.